Chapter 2 Physics Of Sedimentation Mit Opencourseware-PDF Free Download
Part One: Heir of Ash Chapter 1 Chapter 2 Chapter 3 Chapter 4 Chapter 5 Chapter 6 Chapter 7 Chapter 8 Chapter 9 Chapter 10 Chapter 11 Chapter 12 Chapter 13 Chapter 14 Chapter 15 Chapter 16 Chapter 17 Chapter 18 Chapter 19 Chapter 20 Chapter 21 Chapter 22 Chapter 23 Chapter 24 Chapter 25 Chapter 26 Chapter 27 Chapter 28 Chapter 29 Chapter 30 .
TO KILL A MOCKINGBIRD. Contents Dedication Epigraph Part One Chapter 1 Chapter 2 Chapter 3 Chapter 4 Chapter 5 Chapter 6 Chapter 7 Chapter 8 Chapter 9 Chapter 10 Chapter 11 Part Two Chapter 12 Chapter 13 Chapter 14 Chapter 15 Chapter 16 Chapter 17 Chapter 18. Chapter 19 Chapter 20 Chapter 21 Chapter 22 Chapter 23 Chapter 24 Chapter 25 Chapter 26
Physics 20 General College Physics (PHYS 104). Camosun College Physics 20 General Elementary Physics (PHYS 20). Medicine Hat College Physics 20 Physics (ASP 114). NAIT Physics 20 Radiology (Z-HO9 A408). Red River College Physics 20 Physics (PHYS 184). Saskatchewan Polytechnic (SIAST) Physics 20 Physics (PHYS 184). Physics (PHYS 182).
DEDICATION PART ONE Chapter 1 Chapter 2 Chapter 3 Chapter 4 Chapter 5 Chapter 6 Chapter 7 Chapter 8 Chapter 9 Chapter 10 Chapter 11 PART TWO Chapter 12 Chapter 13 Chapter 14 Chapter 15 Chapter 16 Chapter 17 Chapter 18 Chapter 19 Chapter 20 Chapter 21 Chapter 22 Chapter 23 .
Lecture 4: Sedimentation Dr. Fahid Rabah 1. 4. Sedimentation in water Treatment 4.1Definition of Sedimentation: It is the process of removing solid particles heavier than water by gravity force. .
research hoped to discover how current sedimentation rates in North Carolina affect water supply and reservoir management. This paper will review major study findings, including current data availability, sedimentation rates, and monitoring and sedimentation prevention practices. It will then prov
CIVL 1112 Water Treatment - Sedimentation 6/7. Sedimentation Example 3 If the settling velocity of the floc particles is 0.055 cm/s, determine the area of the sedimentation tank. Assume a factor of safety of 1
Equilibrium Sedimentation & Sedimentation Velocity: Random Walks in the presence of forces.
5. 7 Horizontal Flow Sedimentation Tank 51 5. 8 Radial and Vertical Flow Sedimentation Tanks 52 5. 9 Sedimentation Tank — Typical Design 54 5.10 Sedimentation Tank - Simple Inlet & Outlet Arrangements 57 5.11 Tilted Plate Clarifier 59 5.12 Rapid Sand Filter - Main Features 62 5.13 Rapid Filter - Typical Design 63 5.14 Declining Rate Operation 68
sedimentation could be beneficial for system compliance. Effect on Turbidity Sedimentation may remove suspended solids and reduce turbidity by about 50 to 90 percent, depending on the nature of the solids, the level of pretreatment provided, and the design of the clarifiers. Common values are in the 60 to 80 percent range (Hudson, 1981).
Sedimentation tank at the Drøbak wastewater treatment plant . To simulate the sedimentation process, we use such initial conditions as: inlet - velocity inlet, outlet - outflow. Design of the tank was created by GAMBIT software, based on the original geometry of the sedimentation tank. CFD models are used to describe the behavior of
1.1 Sedimentation tank Sedimentation tank is very important unit in water and wastewater treatment plants. It works on the principle of gravity. In sedimentation tank if the velocity of flow is low then particles having a tendency to move towards bottom due to gravity and settle down. Therefore, a sludge layer forms in
processes involved in the plant, primary sedimentation tank has a greater potential to remove more TSS (Total Suspended Solids), COD or BOD with a less operational cost. (Water Environment Federation, 2005) This project will only focus on primary sedimentation tank. The earliest theory applied to design the sedimentation unit was the
Advanced Placement Physics 1 and Physics 2 are offered at Fredericton High School in a unique configuration over three 90 h courses. (Previously Physics 111, Physics 121 and AP Physics B 120; will now be called Physics 111, Physics 121 and AP Physics 2 120). The content for AP Physics 1 is divided
General Physics: There are two versions of the introductory general physics sequence. Physics 145/146 is intended for students planning no further study in physics. Physics 155/156 is intended for students planning to take upper level physics courses, including physics majors, physics combined majors, 3-2 engineering majors and BBMB majors.
Physics SUMMER 2005 Daniel M. Noval BS, Physics/Engr Physics FALL 2005 Joshua A. Clements BS, Engr Physics WINTER 2006 Benjamin F. Burnett BS, Physics SPRING 2006 Timothy M. Anna BS, Physics Kyle C. Augustson BS, Physics/Computational Physics Attending graduate school at Univer-sity of Colorado, Astrophysics. Connelly S. Barnes HBS .
PHYSICS 249 A Modern Intro to Physics _PIC Physics 248 & Math 234, or consent of instructor; concurrent registration in Physics 307 required. Not open to students who have taken Physics 241; Open to Freshmen. Intended primarily for physics, AMEP, astronomy-physics majors PHYSICS 265 Intro-Medical Ph
About the husband’s secret. Dedication Epigraph Pandora Monday Chapter One Chapter Two Chapter Three Chapter Four Chapter Five Tuesday Chapter Six Chapter Seven. Chapter Eight Chapter Nine Chapter Ten Chapter Eleven Chapter Twelve Chapter Thirteen Chapter Fourteen Chapter Fifteen Chapter Sixteen Chapter Seventeen Chapter Eighteen
18.4 35 18.5 35 I Solutions to Applying the Concepts Questions II Answers to End-of-chapter Conceptual Questions Chapter 1 37 Chapter 2 38 Chapter 3 39 Chapter 4 40 Chapter 5 43 Chapter 6 45 Chapter 7 46 Chapter 8 47 Chapter 9 50 Chapter 10 52 Chapter 11 55 Chapter 12 56 Chapter 13 57 Chapter 14 61 Chapter 15 62 Chapter 16 63 Chapter 17 65 .
HUNTER. Special thanks to Kate Cary. Contents Cover Title Page Prologue Chapter 1 Chapter 2 Chapter 3 Chapter 4 Chapter 5 Chapter 6 Chapter 7 Chapter 8 Chapter 9 Chapter 10 Chapter 11 Chapter 12 Chapter 13 Chapter 14 Chapter 15 Chapter 16 Chapter 17 Chapter
Chapter 3 Chapter 4 Chapter 5 Chapter 6 Chapter 7 Chapter 8 Chapter 9 Chapter 10 Chapter 11 Chapter 12 Chapter 13 Chapter 14 Chapter 15 Chapter 16 Chapter 17 Chapter 18 Chapter 19 Chapter 20 . Within was a room as familiar to her as her home back in Oparium. A large desk was situated i
The Hunger Games Book 2 Suzanne Collins Table of Contents PART 1 – THE SPARK Chapter 1 Chapter 2 Chapter 3 Chapter 4 Chapter 5 Chapter 6 Chapter 7 Chapter 8. Chapter 9 PART 2 – THE QUELL Chapter 10 Chapter 11 Chapter 12 Chapter 13 Chapter 14 Chapter 15 Chapter 16 Chapter 17 Chapt
This study uses the Mazowe Catchment area as a case study in analyzing river and reservoir sedimentation and its impact on water quality. Sedimentation in the rivers and reservoirs within the Mazowe Catchment area has become a major challenge for the policy makers as well as the water managers. 1.1 Study areaCited by: 12Publish Year: 2018Author: Colleta Tundu, Michael James Tumbare,
While no dam has ever failed as direct result of sedimentation issues, it does impact the safety of dams. Sedimentation can alter reservoir routing, complicate the management of seasonal flood inflow, reduce spillway discharge capacity, alter reservoir ice mat formation and increase loads on
2. Develop computer models for the simulation and prediction of reservoir sedimentation processes Extensive literature exists on the subject of reservoir sedimentation. The book by Morris and Fan (1997), entitled Reservoir Sedimentation Handbook is an excellent refere
very little know about the sedimentation rates affecting them. To improve the reservoir and irrigation management it is important to make estimations about the reservoir life expectancy. A good method to estimate the sedimentation of a reservoir is by performing a bathymetric survey. But, t
May 13, 2019 · The erosion and sedimentation study will involve collecting and summarizing information under . Hydrologic Impact information: classification of when/if the erosion occurs during extreme . volumes within the reservoir. Identified sedimentation
sedimentation in the lower reaches of Clower Creek and thence into the Bay. Sarasota County authorized this sedimentation analysis to determine the estimated frequency of weir maintenance and estimate the change in sedimentation as development occurred. Three conditions were evaluated including predevelopment, existing and proposed conditions.
Hydrometry — Methods for assessment of reservoir sedimentation Hydrométrie — Méthodes d'évaluation de la sédimentation dans les réservoirs INTERNATIONAL STANDARD ISO 6421 First edition 2012-08-01 . 8 Topographic survey using a cross-sectional (range line) method .
times a proper understanding of sedimentation tank behavior is essential for proper tank design and operation. Generally, sedimentation tanks are characterized by interesting hydrody-namic phenomena, such as density waterfalls, bottom currents and surface return currents, and are also sensitive to temperature fluctuations and wind effects.
strong Ph.D /strong . in Applied Physics strong Ph.D /strong . in Applied Physics with Emphasis on Medical Physics These programs encompass the research areas of Biophysics & Biomedical Physics, Atomic Molecular & Optical Physics, Solid State & Materials Physics, and Medical Physics, in
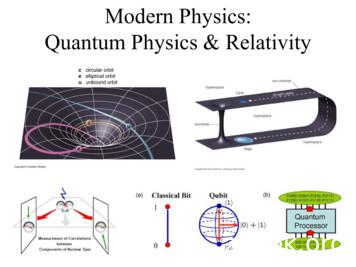
Modern Physics: Quantum Physics & Relativity. You can’t get to Modern Physics without doing Classical Physics! The fundamental laws and principles of Classical Physics are the basis Modern Physics
Ib physics hl ia. Ib physics hl data booklet. Ib physics hl notes. Ib physics hl topics. Ib physics hl textbook. Ib physics hl past papers. Ib physics hl grade boundaries. If you are watching this program, you are probably thinking of taking IB Economics or are currently enrolled in the
Mary Barton A Tale of Manchester Life by Elizabeth Cleghorn Gaskell Styled byLimpidSoft. Contents PREFACE1 CHAPTER I6 CHAPTER II32 CHAPTER III51 CHAPTER IV77 CHAPTER V109 CHAPTER VI166 CHAPTER VII218 i. CHAPTER VIII243 CHAPTER IX291 CHAPTER X341 CHAPTER XI381 CHAPTER XII423 CHAPTER XIII450 CHAPTER XIV479 CHAPTER XV513 CHAPTER XVI551
Part Two: Heir of Fire Chapter 36 Chapter 37. Chapter 38 Chapter 39 Chapter 40 Chapter 41 Chapter 42 Chapter 43 Chapter 44 Chapter 45 Chapter 46 Chapter 47 Chapter 48 Chapter 49 Chapter 50 Chapter 51 . She had made a vow—a vow to free Eyllwe. So in between moments of despair and rage and grief, in between thoughts of Chaol and the Wyrdkeys and
510 racking the AP Physics C ExamC PHYSICS C Physics C has two exams: Physics C (Mechanics) and Physics C (Electricity & Magnetism): Physics C (Mechanics) Physics C (Electricity & Magnetism) First 45 min. Sec. I, Multiple Choice Sec. I, Multiple Choice 35 questions 35 questions Second 45 min. Sec. II, Free-Response
May 15, 2008 · CHAPTER THREE CHAPTER FOUR CHAPTER FIVE CHAPTER SIX CHAPTER SEVEN CHAPTER EIGHT CHAPTER NINE CHAPTER TEN CHAPTER ELEVEN . It is suggested that there is a one-word key to the answer among the four lofty qualities which are cited on every man's commission. . CHAPTER TWO. CHAPTER THREE.
the secret power by marie corelli author of "god's good man" "the master christian" "innocent," "the treasure of heaven," etc. chapter i chapter ii chapter iii chapter iv chapter v chapter vi chapter vii chapter viii chapter ix chapter x chapter xi chapter xii chapter xiii chapter xiv chapter xv
PHYSICS 181 Physics I – Mechanics Lab 4 credits . PHYSICS 185 Freshman Colloquium 1 credit . Spring. PHYSICS 182 Physics II – Electricity and Magnetism Lab 4 credits . PHYSICS 186 Freshman Colloquium 1 credit . For special circumstances, your advisor can authorize an alternate introductory sequence. 2. Sophomore Sequence. Fall
21 years of experience teaching Physics at Louisiana State University and California State University Stanislaus. Courses taught include: General Physics of Physics Majors (PHYS 1201/02) General Physics Laboratory for Physics Majors (PHYS 1208/09) General Physics (PHYS 2001/02) Introductory Physics for Technical Students (PHYS 2101/02)