DAV PUBLIC SCHOOL, JHARSUGUDA QUESTIONS BANK
DAV PUBLIC SCHOOL, JHARSUGUDAQUESTIONS BANK CLASS-XI.Real Number(1Mark)1.The LCM of two numbers is 760 and their product is 6080. Find their HCF.2. Is it possible for the LCM and HCF of numbers to be 378 and 18 respectively?3. Determine the values of p and q so that the prime factorisation of 2520 is expressible as23 x 3p x q x 73.Find the value of (-1)n (-1)2n (-1)2n 1 (-1)4n 1 , where n is positive odd integer.4. If 793800 23 x 3m x 5n x 72, find the value of m and n.435. The decimal expansion of the rational number 24 53 will terminate after how many places ofdecimals?6. Find the least prime factor of a b if the least prime factors of a and b are 3 and 7 respectively.7. Explain why 3 5 7 7 is a composite number.8. If two positive integers a and b are written as a x3y2and b xy3; x, y are prime numbers thenfind the HCF(a,b).9. What is the LCM of p and q where p a3b2 and q b3a2 ?10. A number N when divided by 15 gives the remainder 4. What is the remainder when the samenumber is divided by 5?11. Euclid’s division lemma states that for two positive integers a and b, there exist unique integersq and r such that a b q r. What condition r must satisfy ?12. After how many places of decimals will the decimal expansion of 23457/2 3 x 54 terminate?13. State whether 6/200 has terminating or non-terminating repeating decimal expansion.14. Find the (HCF LCM) for the numbers 50 and 20.(2Marks)1. Show that any positive even integer can be written in the form of 6q,6q 2 or6q 4 where q is an integer2. Find the prime factorisation of the denominator of the of the rational number equivalent to 8.39.3. If HCF(6,a) 2 and LCM(6,a) 60 then find a.4. Show that the numbers 143 and 187 are not coprime.5. Determine whether the following number have a terminating decimal expansion or non17terminating repeating decimal expansion: 3125 .6. If two positive integers x and y are expressible in terms of primes as x p2 q3and y p3 q, what can you say about their LCM and HCF. Is LCM a multipleof HCF ? Explain.
7. Find the least number that is divisible by all numbers between 1 and 10 (both inclusive).8. Given that HCF (306, 657) 9, find LCM (306, 657).9. What type of decimal expansion will 69/60 represent? After how many Places will the decimalexpansion terminate?10. Find the H.C.F. of the smallest composite number and the smallest prime number.11. State Euclid’s Division Lemma and hence find HCF of 16 and 28.12. State fundamental theorem of Arithmetic and hence find the unique factorisation of 120.13. Find the HCF of 867 and 255. Using Euclid’s division algorithm.14. given that LCM (26, 169) 338, find HCF (26,169).15. Express 32760 as product of its prime factors using factor tree.16. Can the numbers 6n, n being a natural number end with the digit 5? Give reasons.17. Find the least number that is divisible by first five even numbers.(3Marks)1. Show that n2 leaves the remainder 1 when divided by 8, where n is an odd positive integer.2. Use Euclid's division lemma show that the square of any positive integer is either of the form5m,5m 1 or 5m 4 for some integer m.2413. If4000 2412𝑚 5𝑛,find the values of m and n where m and n are non negative integers. Hence writeits decimal expansion without actual division.4.Prove that 3 5 2 is an irrational number.5. A rational number in its decimal expansion is 327.7081.What can you say about the prime𝑝factors of q, when this number is expressed in the form 𝑞 ? Give reasons.6. If n is an odd integer, then show that nn – 1 is divisible by 8.7. Use Euclid’s division algorithm to find the HCF of 441, 567, and 693.8. Show that 12n cannot end with the digit 0 or 5 for any natural number n.9. On a morning walk, three persons step off together and their steps measure 40 cm, 42 cm and45 cm, respectively. What is the minimum distance each should walk so that each can cover thesame distance in complete steps?10. Prove that one of any three consecutive positive integers must be divisible by 3.11. For any positive integer n, prove that n3 – n is divisible by 6.12. If d is the HCF of 45 and 27, find x and y satisfying d 27 x 45 y.13. Pens are sold in pack of 8 and notepads are sold in pack of 12. Find the least number ofpacks of each type that one should buy so that there are equal number of pen and notepads14. Find the least positive integer which on adding 1 is exactly divisible by 126 and 60015. A boy with collection of marbles realizes that if he makes a group of 5 or 6 marbles at a timethere are always two marbles left. Can you explain why the boy can’t have prime numbers ofmarbles?16. Show that 571 is a prime number.
17. Prove that no number of the type 4K 2 can be a perfect square18. Explain why 7 11 13 13 and 7 6 5 4 3 2 1 5 are composite numbers.19. If the HCF of 210 and 55 is expressible in the form 210 5 55y then find y.20. If a 4q r then what are the conditions for a and q. What are the values that r can take?21. What is the smallest number by which 5- 3 be multiplied to make it a rational no? Also findthe no. so obtained.22. Prove that n2 n is even for every positive integer n.23. Prove that 6 10 11 is an irrational number.24. Show that 1/ 3 is irrational.25.Find the greatest number of 6 digits exactly divisible by 24, 15 and 36.26.Show that 9n cannot end with the digit 2 for any n ϵ N.27.Find the largest number which divides 318 and 739 leaving remainder 3 and 4 respectively.328. Prove that 6 is not a rational number.29. Show that any positive odd integer is of the form 8q 1, 8q 3, 8q 5 or 8q 7, where q is someinteger.30. The following real numbers have decimal expansions as given below. In each case decide,𝑝whether they are rational or not. If they are rational and of the form, 𝑞 what can you say aboutthe prime factor of q.(i) 0.0875 (ii) 0.130130013000130000. (iii) 0.142857(4Marks)1. Is square root of every non square number always irrational? Find the smallest natural numberwhich divides 2205 to make its square root a rational number.2. Find HCF of 378,180 and 420 by prime factorisation method. Is HCF X LCM of the threenumbers equal to the product of the three numbers?3. If n is an odd integer then show that n2 – 1 is divisible by 8.4. Show that one and only one out of n, n 2 and n 4 is divisible by 3, where n is any positiveinteger.5. Prove that cube of any positive integer is of the form 4m, 4m 1 or 4m 3 for some integer m.6. Using Euclid’s division algorithm, find which of the following pairs of numbers are co-prime:(i) 231, 396 (ii) 847, 21607. Show that cube of any positive integer is of the form 4m, 4m 1 or 4m 3, for some integerm.8. Use Euclid’s division lemma to show that the cube of any positive integer is of the form 9m ,9m 1 or 9m 8.
9. The length breadth and height of a room are 8m 25cm, 6m 75cm and 4m 50cm respectively.Determine the longest rod which can measure the three dimensions of the room exactly.10.Show that p q is irrational, where p, q are primes.11. Show that cube of any positive integer is of the form 4m, 4m 1 or 4m 3, for some integer m.II. Polinomials(1Mark)1. Write the quadratic polynomial having zeroes 1 and –2.2. Write the quadratic polynomial whose sum of zeroes is 3 and product of zeroes is –2.3. If (x 1) is a factor of x2 – 3ax 3a – 7, then find the value of a .4. How many polynomials are there having zeroes –2 and 5.5. Write the quadratic polynomial p(y) with –15 and –7 as sum and one of the zeroesrespectively.6. If 1 is a zero of the polynomial p(x) ax2– 3(a – 1)x – 1, then find the value of a .7. If – 4 is a zero of the polynomial x2 – x – (2 2k), then find the value of k.8. Write the quadratic polynomial having sum and product of zeroes 1 and –2 respectively.9. If (x 1) is a factor of x2 – 3ax 3a – 7, then find the value of a .10. Find the degree of the polynomial (x 1)(x2 – x – x4 1) .11. Find a quadratic polynomial, the sum and product of whose zeroes are 0 and 5 respectively.12. Find the quadratic polynomial, the sum and product of whose zeroes are 4 and 1,respectively13. Find the quadratic polynomial, the sum and product of whose zeroes are 2 and 3respectively.14. Find the remainder when p(x) x3-6x2 2x-4 is divided by 1 -2x.15. Find the remainder when x51 51 is divided by (x 1).16. Find all the integral zeros of x3-3x2-2x 617. On dividing 2x2 3x 1 by a polynomial g(x), the quotient and the remainder were 2x 1 and3 respectively. Find g (x).18. Find the zeroes of 2x3–11x2 17x – 6.19. Find the quadratic polynomial, the sum and the product of whose zeroes are1/2, and –2 resp.20. Find the values of m and n for which x 2 and –3 are zeroes of the polynomial: 3x2–2mx 2n21. Check whether x2 4 is factor of x4 9x2 20.22. Find the polynomial whose sum and product of the zeros are - ½ and ½ respectively.23. Can y 1 be the remainder on division of a polynomial p(y) by y - 5 ? Give reason.24. If α ,β are the zeros of f (x) px2 – 2x 3p and α β α β, then find the value of p .25. If one zero of the quadratic polynomial p(x) x2 4kx - 25 is negative of the other, find thevalue of k.26. Answer the following questions in one word, one sentence or as per the exact requirement ofthe question.
i) If one zero of the quadratic polynomial x2 x – 2 is -2, find the other zero.iii) Find the quadratic polynomial whose zeros are -3 and -5 .(2 MARKS)1. Divide the polynomial (x2 1) by (x –1) and verify the division algorithm.2. If one zero of 2x2 – 3x k is reciprocal to the other, then find the value of k.3.Find the value of p for which the polynomial x3 4x2 – px 8 is exactly divisible by (x – 2) .4. If 1 is a zero of the polynomial p(x) ax2– 3(a – 1)x – 1, then find the value of a .5. If –4 is a zero of the polynomial x2 – x – (2 2k), then find the value of k.6.What must be subtracted from the polynomial 8x4 14x3 x2 7x 8 so that the resultingpolynomial is exactly divisible by 4x2 – 3x 2 ?7.If the remainder on division of x3 2x2 k x 3 by x - 3 is 21. Find the quotient and the value ofk.8.If α and β are the zeros of the polynomial f (x) x2 – 3x 2, then find the value 1/α 1/β .9.If a and 1/a are the zeros of polynomial 4x2 -2x (k-4), then find the value of k.10.Find the zeros of the polynomial 5y2 -11y 2.(3 Marks)1. Find a quadratic polynomial each with the given zeros as sum and the product of its zerosrespectively(a) ¼, -1(b) 2 , 1/32. Using division algorithm, find the quotient and the remainder on dividing f(x) by g(x) , wheref(x) 6x3 13x2 2x and g(x) 2x 13. If x 1 is a factor of 2x3 ax3 2bx 1, then find the values of a and b given that 2a–3b 4.4. If α , β are the zeros of 2y2 7y 5 write the value of α β α β.5. Find the zeros of a quadratic polynomial 5x2- 4 -8x and verify the relationship between thezeros and the coefficients of the polynomial.6. If α, β are the zeros of the poly. f(x) x2-px q, find the value of(a) α2 β2(b)1/α 1β7.Find all the zeros of p(x) x3 – 9x2 – 12x 20 if (x 2) is a factor of p(x).8.If (x a) is a factor of two polynomials x2 p x q and x2 mx n then prove thata n-q/m-p.9.Find the zeros of 4 3x2 5x - 2 3 and verify the relation between the zeros and coefficient ofthe polynomial.10.If a and β are the zeros of the quadratic polynomial f (t) t2 – p(t 1)- c, show that(α 1) (β 1) 1 – c.
11. If the zeros of the quadratic polynomial x2 (a 1) x b are 2 and -3, then find a and b.(4 MARKS)1. Find all the zeros of 2x4-9x3 5x2 3x-1, if two of its zeros are 2 3 & 2- 32.If the polynomial 6x4 8x3 17x2 21x 7 is divided by another polynomial 3x2 4x 1, theremainder comes out to be (ax b), find a and b.3.Find all other zeroes of the polynomial p(x) 2x3 3x2 – 11x – 6, if one of its zero is –3.4. Given that x – 5 is a factor of the cubic polynomial x3–3 5x2 13x –3 5 ,find all the zeroes ofthe polynomial5. Given that 2 is a zero of the cubic polynomial 6x3 2 x2–10x –4 2 , find its other two zeroes.6. Find k so that x2 2x k is a factor of 2x4 x3–14 x2 5x 6. Also find all the zeroes of the twopolynomials.7.Obtain all other zeros of the polynomial x4 -3x3 – x2 9x – 6, if two of its zeros are 3 and - 3.8.Find the cubic polynomial with the sum ,sum of the products of its zeroes taken two at a time,and the products of its zeroes as -3, -8 and 2 respectively.9.Given that 3 is a zero of the polynomial x3 x2- 3x – 3, find its other two zeroes.10.If the zeros of the polynomial f(x) x3 - 3x2 - 6x 8 are of the form a -b, a, a b, find all thezeros.11. If α and β are the zeros of the polynomial f(x) 4x2 -5x 1, find a quadratic polynomialwhose zeros are α2/ β and β2/α .III. Pair of Linear Equations in Two Variables(1Mark)1. Solve x – y 4, x y 10 and hence find the value of p when y 3x –p.3. For which value(s) of k will the pair of equations kx 3y k – 3 ; 12x ky k have no solution?4. Find the value of k for which the lines (k 1) x 3ky 15 0 and 5x k y 5 0 arecoincident.5. What types of lines do the pair of eqn. x a and y b represent graphically.6. How many solutions does the pair of equations x 2y 3 and ½ x y -3/2 0 have?7. Find the value of k for which the system of equations 2x y -3 0 and 5x k y 7 0 has nosolution.8. Find the value of k for which the system of equations 2x 3y 7 and8x (k 4)y – 28 0 has infinitely many solution.9. Give linear equations which is coincident with 2 x 3y - 4 010. What is the value of a for which (3, a) lies on 2x – 3y 5.11. The sum of two natural nos. is 25 and their difference is 7. Find the nos.
(2Marks)1. For which values of p and q, will the following pair of linear equations have infinitely manySolutions?4x 5y 2 ; (2p 7q) x (p 8q) y 2q – p 1.2. Solve the following pair of linear equations: 21x 47y 110; 47x 21y 1623. The angles of a cyclic quadrilateral ABCD are A (6x 10) , B (5x) C (x y) ,D (3y –10) . Find x and y, and hence the values of the four angles.4. Check graphically whether the pair of eq. 3x 2y – 4 0 and 2x – y – 2 0 is consistent. Alsofind the coordinates of the points where the graphs of the lines of equations meet the y-axis.5. The angles of a triangle are x, y and 40 . The difference between the two angles x and y is30 . Find x and y.6. If x a and y b is the solution of the equation x-y 2 and x y 4 then findthe value of a and b.7. In ABC, A x0, B 3 x0 and C y0. If 3y-5x 30 prove that the triangle is right angled.8. If 3x 7y -1 and 4y-5x 14 0, find he values of 3x-8y and y/x -2.9. Is the pair of equations x-y 5 and 2y-x 10 inconsistent? Justify your answer.10. If the system of equations 4x- y 3 and (2k-1)x (k-1)y 2k 1 is inconsistent,then find k.11. Solve the pair of linear equations x – y 2 and x y 2. Also find p if p 2x 312. For what value of K the following system of equation are parallel.2x Ky 10, 3x (k 3) y 12(3 Marks)1. Draw the graphs of the pair of linear equations x – y 2 0 and 4x – y – 4 0. Calculatethe area of the triangle formed by the lines so drawn and the x-axis.2. For which value(s) of λ , do the pair of linear equationsλx y λ2 and x λy 1 have( i) no solution?(ii) infinitely many solutions?(iii) a unique solution?3. For which values of a and b, will the following pair of linear equations have infinitely manysolutions? x 2y 1 (a – b)x (a b)y a b – 25. Two years ago, Salim was thrice as old as his daughter and six years later, he will be fouryears older than twice her age. How old are they now?6. The age of the father is twice the sum of the ages of his two children. After 20 years, his agewill be equal to the sum of the ages of his children. Find the age of the father.7. Two numbers are in the ratio 5 : 6. If 8 is subtracted from each of the numbers, the ratiobecomes 4 : 5.Find the numbers.8. There are some students in the two examination halls A and B. To make the number ofstudents equal in each hall, 10 students are sent from A to B. But if 20 students are sent fromB to A, the number of students in A becomes double the number of students in B. Find thenumber of students in the two halls.9. A shopkeeper gives books on rent for reading. She takes a fixed charge for the first two days,and an additional charge for each day thereafter. Latika paid Rs 22 for a book kept for sixdays, while Anand paid Rs 16 for the book kept for four days. Find the fixed charges and thecharge for each extra day.10. In a competitive examination, one mark is awarded for each correct answer while ½ mark isdeducted for every wrong answer. Jayanti answered 120 questions and got 90 marks. Howmany questions did she answer correctly?
.11. Jamila sold a table and a chair for Rs 1050, thereby making a profit of 10% on the table and25% on the chair. If she had taken a profit of 25% on the table and 10% on the chair shewould have got Rs1065. Find the cost price of each.[ 500, 400]12. It can take 12 hours to fill a swimming pool using two pipes. If the pipe of larger diameter isused for 4hours and the pipe of smaller diameter for 9 hours, only half the pool can befilled.How long would it take for each pipe to fill the pool separately?[ 20, 30]13. Ankita travels 14 km to her home partly by rickshaw and partly by bus. She takes half an hourif she travels 2 km by rickshaw, and the remaining distance by bus. On the other hand, if shetravels 4 km by rickshaw and the remaining distance by bus, she takes 9 minutes longer. Findthe speed of the rickshaw and of the bus.14. A person, rowing at the rate of 5 km/h in still water, takes thrice as much time in going 40 kmupstream as in going 40 km downstream. Find the speed of the stream.15. Find the value of p and q for which the system of equations represent coincident lines2x 3y 7, (p q 1)x (p 2q 2)y 4(p q) 116. The larger of two supplementary angles exceeds the smaller by 180, find them.17. A chemist has one solution which is 50% acid and a second which is 25% acid. Howmuch of each should be mixed to make 10 litres of 40% acid solution.18. When 6 boys were admitted & 6 girls left the percentage of boys increased from 60%to 75%. Find the original no. of boys and girls in the class.19. Solve the following equations by the method of cross –multiplication:mx - ny m2 n2 and x y 2m19.Half the perimeter of a rectangular garden, whose length is 4m more than its widthis 36m .Find the dimensions of the garden.20.If x 1 is a factor of 2x3 ax2 2bx 1, then find the values of a and b given that2a -3b 4.21.The age of the father is twice the sum of the ages of his two children. After 20 years, his age will beequal to the sum of the ages of his children. Find the age of the father.22. The larger of two supplementary angles exceeds thrice the smaller by 20 degrees. Find them.23. Check graphically whether the pair of linear equations 3x 5y 15, x – y 5 is consistent.Also check whether the pair is dependent.(4 Marks)1. For which value(s) of k will the pair of equations kx 3y k – 3 ; 12x ky k have no solution?2. Two rails are represented by the equations x 2y – 4 0 and 2x 4y – 12 0. Represent thissituation geometrically.3. Solve for p and q: [p q ] / pq 2 and [p-q ] / pq 64. Solve for x and y : 6 /[x y] 7/ [x-y] 3 ; 1/ 2[x y] 1/ 3[x-y]5. Form a pair of linear equations for : The sum of the numerator and denominator of fraction is 3less than twice the denominator. If the numerator and denominator both are decreased by 1,the numerator becomes half the denominator.6. Amar gives Rs. 9000 to some athletes of a school as scholarship every month. Had there been20 ore athletes each would have got Rs. 160 less. Form a pair of linear equations for this.7. Dinesh in walking along the line joining (1, 4) and (0, 6), Naresh is walking along the linejoining (3, 4,) and (1,0). Represent on graph and find the point where both of them cross eachother.
8. Form a pair of linear equati
QUESTIONS BANK CLASS-X I.Real Number (1Mark) 1.The LCM of two numbers is 760 and their product is 6080. Find their HCF. 2. Is it possible for the LCM and HCF of numbers to be 378 and 18 respectively? 3. Determine t
03 mathematics fun with maths dav/cbse 04 hindi akshar prichay dav/cbse 05 rhymes rhythmic rhyme book dav/cbse 06 drawing fun with colors'a' dav/cbse sr. no subject t rle/name of book publication 01 english fun with english dav/cbse 02 english integrated activity book dav/cbse 03 mathematics ki ndergarten math ematics dav/cbse 04' hindi bal .
DAV PUBLIC SCHOOL, JHARSUGUDA CLASS - VIII CHAPTER 1 TO 16 CH-1. SQUARES AND SQAURE ROOTS 1Mark Questions 1. The least numbers which must be subtracted from 4360 to make it a perfect square is _. 2. If 140 x 315 1015,then x is equal to _. 3. The value of (0.9) 2- (0.1) is_. 4. The greatest number of 4 digit which is a perfect square .
DAV PUBLIC SCHOOL, JHARSUGUDA QUESTION BANK SUB –MATHEMATICS CLASS – VI Natural numbers and whole numbers Section A – 1 mark each 1. Which is the Roman numeral of 49? a)XCVII b) XLIX c) LXXIX d) XCI 2. What is the smallest whole number? a) 0 b) 1 c) 9 d) none of these .
DAV Publication Division, New Delhi 7 Maths Secondary Mathematics DAV Publication Division, New Delhi 8 Science The Living World DAV Publication Division, New Delhi 9 S.St. We & Our World DAV Publication Division, New Delhi 10 Atlas To continue with the same Atlas as in Class VI Madhuban Educational Books 11 Drawing & Painting Step By Step
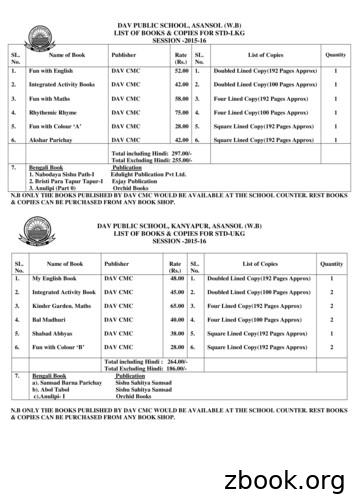
LIST OF BOOKS & COPIES FOR STD-UKG SESSION -2015-16 SL. No. Name of Book . My English Book DAV CMC 48.00 1. Doubled Lined Copy(192 Pages Approx) 1 2. Integrated Activity Book DAV CMC 45.00 2. Doubled Lined Copy(100 Pages Approx) 2 . (40 Page s Approx) 8 5. Primary Maths DAV CMC 102.00 6. Bhasha Madhuri DAV CMC 60.00 .
DAV Silicone Wristbands: 50 wristbands for 25 Purchase banners and wristbands: DAV Sales sales@dav.org 877-426-2838, Ext. 3252 3. Download, print and customize your DAV D4URC event poster. Click here to download the customizable event poster. Consider placing a copy of the poster in your newsletter or on your website. 4.
SUB - ENGLISH BOOK PRESCRIBED: 1. Class VIII English Literature Book (DAV CMC Publications) 2. Class VIII English Practice Book (DAV CMC Publications) 3. Class VIII MY English Reader Book (DAV CMC Publications) SPLIT UP SYLLABUS FOR MONTH CHAPTERS / TOPIC TO BE TAUGHT ANNUAL EXAMINATION MI
STATEMENT OF PURPOSE NSF.DAORV. G 3. THE DAV NATIONAL SERVICE FOUNDATION Since DAV (Disabled American Veterans) was founded in 1920 as an organization of veterans helping veterans, it has served the nation’s ill and injured heroes tirelessly . Increasing public awareness about DAV’s