Mutually Coupled Inductors. Coupling Coefficient. Power .
Lecture notes in Theory of electrical engineering.Assoc. Prof. Dr. Boris EvstatievMutually coupled inductors. Coupling coefficient. Power and energyof mutually coupled inductors. Analysis of circuits with mutuallycoupled inductor.6.1. Equivalent circuits of mutually coupled inductorsAs was already mentioned in the second topic, when the magnetic field of one coil reaches a secondone the two inductors are mutually coupled and are characterized by a coefficient of mutualinductance M . Depending on the connection between inductors there are a number of equivalentcircuits which could be used to simplify the circuit analysis.6.1.1. Mutually coupled inductors in seriesConsider there are two inductors L1 and L2 in series, which are magnetically coupled andhave a mutual inductance M . The magnetic field of the two inductors could be aiding oropposing each other, depending on their orientation (fig 6.1).a)b)Fig. 6.1. Mutually coupled inductors and dot convention: a) series aiding inductors; b) seriesopposing inductors.Aiding inductors in series as well as the dot convention are presented in fig. 6.1a. Since theirmagnetic fields aid each other, the KVL for this situation is:dididididiv v 1 v M v 2 v M L1 L M L L2 L M L ( L1 L2 2 M ) LdtdtdtdtdtIn the above equation v M is the voltage drop caused by the mutual inductance M . There aretwo voltage drops v M : one is produced by the additional magnetic flux coming from L1 toL2 and the second one – by the magnetic flux coming from L2 to L1 . Then the equivalentinductance is:LE L1 L2 2 MThe second situation is when the magnetic field of the two coils oppose each other (fig. 6.1b). Then1
Lecture notes in Theory of electrical engineering.the KVL law is:v v 1 v M v 2 v M L1Assoc. Prof. Dr. Boris Evstatievd iLdidididi M L L2 L M L ( L1 L2 2 M ) LdtdtdtdtdtAnd the equivalent inductance is:LE L1 L2 2 M6.1.2. Mutually coupled inductors in parallelConsider two inductors L1 and L2 are connected in parallel and are mutually coupled withmutual inductance M . The voltage applied on the inductors is v S . Once again there are twopossibilities: the magnetic fields of the two inductors could be aiding or opposing each other.a)b)Fig. 6.2. Mutually coupled inductors in parallel: a) aiding inductors; b) opposing inductors.First, we accept that the inductors are aiding each other (fig. 6.2a) and write down two KVLequations:didiv S L1 1 M 2dtdtd i2d i1v S L2 MdtdtNext, the above system is written in matrix form:d i1v S L1 M . dtv S M L2 d i2dtThe determinants are:L M 1 L1 . L2 M 2M L2 1 vS M v S ( L2 M )v S L2L1 v S v S ( L1 M )M vSThe solutions for the current derivatives are:d i 1 1 d i 2 2 dt dt The KVL for the circuit is:i i 1 i2 2 2
Lecture notes in Theory of electrical engineering.Assoc. Prof. Dr. Boris EvstatievThe above equation is differentiated:L L 2. Mdi d i1 d i 2 1 2 v S ( L2 M ) v S ( L1 M ) v S 1 222dt dt dt L1 . L2 ML1 . L2 MThen the equivalent inductance is:2di ( t ) L1 . L2 M di ( t )v S ( t ) L E .dtL1 L2 2. M dtor2L1 . L2 MLE L1 L2 2. MIn a similar manner can be proven that the equivalent inductance of parallel inductors whosemagnetic fields are oppose each other, is:L1 . L2 M 2LE L1 L2 2. M6.1.3. Elimination of mutual inductanceConsider the case when two coils are mutually coupled (fig. 6.3). They could be replaced with anequivalent circuit without mutual inductance and three coils as shown in the figure. To prove thiswe write the system of equations for the original circuit:didiv1 L1 1 M 2dtdtdidiv2 L2 2 M 1dtdtThen we write the system of equations for the equivalent circuit:didiv1 ( L1 M ) 1 M 0dtdtd i2d i0v2 ( L2 M ) Mdtdtd i0 d i1 d i2Consideringwe obtain the same system of equations as for the original circuit: dtdt dtdididididiv1 ( L1 M ) 1 M 1 M 2 L1 1 M 2dtdtdtdtdtd i2d i1d i2d i2d i1v2 ( L2 M ) M M L2 MdtdtdtdtdtIn a similar manner we can prove the circuit for the mutually opposing inductors. a)3
Lecture notes in Theory of electrical engineering.Assoc. Prof. Dr. Boris Evstatievb)Fig. 6.3. Equivalent circuit for: a) aiding inductors; b) opposing inductors.Note that the nodes 1 and 2 of the original circuit may or may not be connected and that doesn’tchange the equivalent circuit.6.1.4. General caseConsider two inductors with mutual inductance which may or may not have an electric connection.If the two inductors are aiding each other, the equivalent circuit is presented in fig. 6.4. The mutualdidiinductance is replaced by two dependent sources M 2 and M 1 , which are opposing thedtdtdirection of the currents.Fig. 6.4.The KVL eqations for both the original and the equivallent circuit is:didiv1 ( t ) L1 1 M 2dtdtdidiv2 ( t ) L2 2 M 1dtdtNext consider the two inductors are opposing each other (fig. 6.5.). The equivallent circuit is thedidisame however this time dependent sources are with a negative sign: M 2 and M 1 .dtdt 4
Lecture notes in Theory of electrical engineering.Assoc. Prof. Dr. Boris EvstatievFig. 6.5.The KVL eqations for both the original and the equivallent circuit is:didiv1 ( t ) L1 1 M 2dtdtd i2d i1v2 ( t ) L2 MdtdtIf the above time domain variables are replaced with phasors, the dependent sources in the equivallent circuits becomes andjωM I 1jωM I 2for aiding inductors and jωM I 1and jωM I 2 for opposing inductors (fig. 6.6).Fig. 6.6.The KVL eqations in complex form for the circuits are: V 1 jω L1 I 1 jωM I 2V 2 jω L2 I 2 jωM I 1where the plus sign corresponds to aiding inductors and the minus sign – to opposing inductors.6.2. Energy in mutually coupled inductorsIt was already demonstrated in the second topic that the energy stored in an inductor is:1W L . L. i 22Let’s consider two mutually coupled inductors (fig. 6.7). The power transferred from the first to thesecond coil is:dipM 12 (t ) i 2 . v M i2 . M 1dt5
Lecture notes in Theory of electrical engineering.Assoc. Prof. Dr. Boris EvstatievFig. 6.7.If we integrate the power from t 1to t 2 the energy is:tIdi1W M 12 p M 12 ( t ) dt i2 . M 1 dt M . i 2 . d i1 . M . i 1 i 2dt2tt0The power transferred form the second to the first coil is:dipM 21 ( t ) i1 . v M i1 . M 2dtThen the transferred energy is:ttId i21W M 12 p M 21 ( t ) dt i1 . Mdt M .i 1 . d i2 . M . i 1 i 2dt2tt0The energy stored in the two coils due to their self-inductance is:11W L1 . L1 .i 12 ,W L 2 . L2 .i 2222Then the total energy stored in two mutually coupled inductors is:11W . L1 . i 12 . L2 . i22 M .i 1 i 222The plus sign corresponds to aiding inductors and the minus – to opposing ones.Since energy usage is always positive we can rewrite the above equation (use equation for opposinginductors) as:11. L1 .i 12 . L2 . i 22 M . i 1 i 2 022or12L1 . i1 L2 i 2) i 1 i2 ( L1 L2 M ) 0( 22Considering ( L1 . i 1 L2 i 2 ) is always positive or zero, then the second term is also greater orequal to zero: L1 L2 M 0This way is defined the coupling coefficient k :Mk L1 L2The coupling coefficient takes values in the range 0 k 1 and shows how good the couplingbetween the two coils is. For coils which are not coupled, k 0 and in case of ideal coupling(only possible in theory) k 1 .t221122116.3. Analysis of circuits with magnetically coupled inductors6.3.1. Kirchhoff’s laws analysisThe analysis of circuits with magnetically coupled inductors could be achieved using an equivallentcircuit without magnetic couples. The analysis using the Kirchhoff’s laws includes creating theequivallent circuit and analyzing it by writing a system of equation whose number is equal to thenumber of unknown currents.6
Lecture notes in Theory of electrical engineering.Assoc. Prof. Dr. Boris EvstatievExample: Estimate the currents for the circuit in fig. 6.8 using the Kirchhoff’s laws.Fig. 6.8.It can be seen that the mutual inductancejωMis given as mutual resistance:jωM j0.5 ΩFirst we are going to create an equivallent circuit by replacing the mutual inductance with dependent source (fig. 6.9). Since both currentsI1 andI2sources are with plus sign.Next we write the system of equations: I 1 I 2 I 3 1 j 0.5 I 3 10 I 1 ( 1 j 2 ) I 2 j 0.5 I 3 j 0.5 I 2 ( 1 j2 ) I 2 0 I 3Fig. 6.9.In matrix form it becomes:[ ][ I 1 11 I 2 10 1 j 20 1 j 1.5 I37][]10j 0.5 1j 0.50enterthe dots, the dependent
Lecture notes in Theory of electrical engineering.Assoc. Prof. Dr. Boris EvstatievThe determinants are: 111 10 1 j2 j 0.5 j0.5 ( 1 j2 ) 10 ( 1 j 1.5 ) j0.5 ( 1 j 1.5 ) j 0.5 10 0 1 j1.5 j 0.5 j 0.5 1 10 j15 j0.5 0.75 j 5 10.25 j 10011 1 1 1 j 2 j 0.5 1 j 1.5 j 0.5 1 j0 1 j 1.5 j 0.5[][][ 1 0 2 10 10 0]1j 0.5 j 0.5j 0.5[] 110 3 10 1 j 2 1 1 j 1.50 1 j 1.5 0And the currents are: 11 j 0.099 j 0.001 A 10.25 j10 j 0.5I2 2 0.024 j0.025 A 10.25 j10 1 j1.5I3 2 0.123 j 0.026 A 10.25 j10 I1 6.3.2. Nodal analysisThe nodal analysis cannot be applied if dependent sources are used. However in certain situationswhere the mutual inductance could be eliminated, the nodal analysis can be applied.Example: Estimate the currents for the circuit in fig. 6.8 using nodal analysis.Considering the two coils have a common end, the mutual inductance could be replaced with anequivallent circuit with three coils (fig. 6.10). Their resistances are:jω L1 j 2 j0.5 j 1.5 Ωjω L2 j 3 j 0.5 j2.5 Ωjω L3 j 0.5 ΩFig. 6.10.Now we can apply nodal voltage analysis. The KCL is:8
Lecture notes in Theory of electrical engineering.Assoc. Prof. Dr. Boris Evstatiev 1 V 1V1V1I 1 I 2 I 3 ¿ 10 j 0.5 1 j1.5 j0.5The node voltage then becomes:1 10 j 0.50.100 j 0.005V 1 0.013 j 0.0621110.407 j1.533 1 j1.5 j 0.5 10 j 0.5And the currents are: 0.987 j 0.062I1 0.099 j 0.001 A10 j0.5 0.013 j 0.062I2 0.025 j0.025 A1 j1.5 0.013 j 0.062I3 0.124 j 0.026 A j 0.5 6.3.3. Mesh analysisThe mesh analysis method can be applied for analysis of circuits with mutual indcutance. Howeverin order to do that the dependent sources should be expressed with the mesh currents. Once this isdone the equations are written according to KVL.Example: Estimate the currents for the circuit in fig. 6.8 using mesh analysis.First we should estimate the branch currents with the mesh currents: I 1 I (k)1 I 2 I (1k ) I (2k ) I 3 I (k)2Then the equivallent dependent sources become (fig. 6.11): ( j 0.5 I 2 j 0.5 I (1k ) I (2k ) j 0.5 I 3 j 0.5 I (k)2Fig. 6.11.The two KVL equations are:9)
Lecture notes in Theory of electrical engineering. Assoc. Prof. Dr. Boris Evstatiev 1 j0.5 I (2k ) I (1k ) ( 10 1 j2 ) I (2k ) (1 j2 ) 1 I (1k ) ( 11 j2 ) I 2(k ) ( 1 j 1.5 )and j 0.5 I (2k ) j 0.5 I (1k ) j 0.5 I (2k ) I (2k ) ( 1 j 2 j 3 j3 ) I (1k ) ( 1 j 2 ) 0 I (1k ) ( 1 j1.5 ) I (2k ) ( 1 j )In matrix form the equations are:[ I (1k ) I (2k )][][]11 j2 ( 1 j 1.5 ) 1 ( 1 j 1.5 )1 j0The determinants are:11 j 2 ( 1 j 1.5 ) 11 j 11 j2 2 1 j1.5 j 1.5 2.25 ¿10.25 j10 ( 1 j 1.5 )1 j[][]() 1 1 1 j1.5 1 j01 j1 1 j 1.5 2 11 j 2 ( 1 j 1.5 ) 0[And the mesh currents are:] 11 j 0.099 j 0.001 10.25 j10 1 j1.5I (2k ) 2 0.123 j 0.026 10.25 j10 I (1k ) Then the branch currents are: I 1 I (k)1 0.099 j 0.001 A I 2 0.099 j 0.001 0.123 j 0.026 0.024 j 0.025 A I 3 0.123 j 0.026 AReferences1. Alexander Ch., Sadiku M. Fundamentals of electric circuits. Fifth edition. McGraw-Hill. 2013.Chapter 13.2. Hayt W., Buck J. Engineering electromagnetics. Sixth edition. McGraw-Hill. 2001. Chapters 5and 9.3. tor10
Mutually coupled inductors in series Consider there are two inductors L1 and L2 in series, which are magnetically coupled and have a mutual inductance M. The magnetic field of the two inductors could be aiding or opposing each other, depending on their orientation (fig 6.1). a) b) Fig. 6.1. Mutually cou
Inductors in Series – No Mutual inductance When inductors are connected in series, the total inductance is the sum of the individual inductors' inductances. L T L 1 L 2 L N Example #1 Three inductors of 10mH, 40mH and 50mH are connected together in a series
SMD Inductors Series All specification & dimensions are subject to change,please call your nearest KLS sales represesntative for update information ORDER INFORMATION Product NO.: KLS1 - -2218 SP32 K-R Inductors SMD INDUCTORS Series Electrical code 1.0 220:.μH Tolerance:K 10%,M 20%. KLS18-SP32 SMD
Abstract: Core loss in inductors can adversely affect system performance. Yet, predicting core loss is a complicated endeavor, especially in complex structures such as coupled inductors. This article examines core loss and the resulting effects that should be considered. The article also discusses how the core loss in coupled inductor design can be
mutually exclusive events determine P(A) given P(A B), P(A B), and P(B) for non-mutually exclusive events interpret a model that represents any combination of mutually exclusive and non-mutually exclusive events represent events that are non-mutually exclusive using a
SMD Inductors Metal Composite Power Inductors MPXV Automotive Grade Part Number System MPX 1 D0520 L 1R5 Series Version Size Code Inductor Inductance Code µH MPXV 1 D0520 5x5x2.0 mm D0530 5x5x3.0 mm D0618 6x6x1.8 mm D0624 6x6x2.4 mm D0630 6x6x3.0 mm D0650 6x6x5.0 mm D
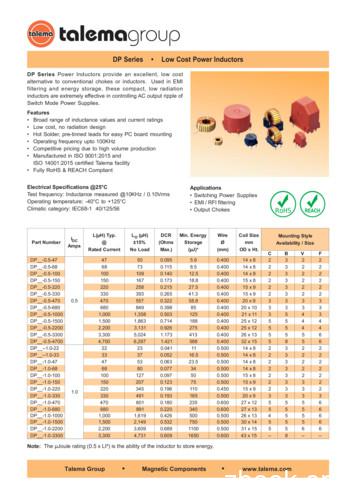
DP Series Power Inductors provide an excellent, low cost alternative to conventional chokes or inductors. Used in EMI filtering and energy storage, these compact, low radiation inductors a
Inductors in series add like resistors in series. Note the total inductance is greater than the individual inductances. Two inductors in parallel: I V I1 L1 I2 L2 Since the inductors are in
Adventure or Extreme Tourism To remote, exotic, sometimes hostile destinations; outside of comfort zones Agritourism Travel to dude ranches, country farms, country inns and rural bed & breakfasts. Gastro-tourism is linked Backpacking - Wilderness Hiking and camping in the backcountry Backpacking –Travel Low-cost, usually international , using public transportation, staying in hostels .