Capacitor And Inductors - MIT OpenCourseWare
Capacitors and inductorsWe continue with our analysis of linear circuits by introducing two new passive andlinear elements: the capacitor and the inductor.All the methods developed so far for the analysis of linear resistive circuits are applicableto circuits that contain capacitors and inductors.Unlike the resistor which dissipates energy, ideal capacitors and inductors store energyrather than dissipating it.Capacitor:In both digital and analog electronic circuits a capacitor is a fundamental element. Itenables the filtering of signals and it provides a fundamental memory element.The capacitor is an element that stores energy in an electric field.The circuit symbol and associated electrical variables for the capacitor is shown onFigure 1.Ci v Figure 1. Circuit symbol for capacitorThe capacitor may be modeled as two conducting plates separated by a dielectric asshown on Figure 2.When a voltage v is applied across the plates, a charge q accumulates on one plate and acharge –q on the other.insulatorplate of area Aq - and thickness s vEd-qsFigure 2. Capacitor model6.071/22.071 Spring 2006, Chaniotakis and Cory1
If the plates have an area A and are separated by a distance d, the electric field generatedacross the plates isE qεΑ(1.1)and the voltage across the capacitor plates isv Ed qdεA(1.2)The current flowing into the capacitor is the rate of change of the charge across thedqcapacitor plates i . And thus we have,dti dq d ε A ε A dvdvv Cdt dt d d dtdt(1.3)The constant of proportionality C is referred to as the capacitance of the capacitor. It is afunction of the geometric characteristics of the capacitor - plate separation (d) and platearea (A) - and by the permittivity (ε) of the dielectric material between the plates.C εAd(1.4)Capacitance represents the efficiency of charge storage and it is measured in units ofFarads (F).The current-voltage relationship of a capacitor isi Cdvdt(1.5)The presence of time in the characteristic equation of the capacitor introduces new andexciting behavior of the circuits that contain them. Note that for DC (constant in time)dvsignals ( 0 ) the capacitor acts as an open circuit (i 0). Also note the capacitor doesdtnot like voltage discontinuities since that would require that the current goes to infinitywhich is not physically possible.If we integrate Equation (1.5) over time we have6.071/22.071 Spring 2006, Chaniotakis and Cory2
tt dv idt C dt dt(1.6) tv 1 i dtC (1.7)t1 i dt v(0)C0The constant of integration v(0) represents the voltage of the capacitor at time t 0.The presence of the constant of integration v(0) is the reason for the memory propertiesof the capacitor.Let’s now consider the circuit shown on Figure 3 where a capacitor of capacitance C isconnected to a time varying voltage source v(t).i(t) v(t)Cv-Figure 3. Fundamental capacitor circuitIf the voltage v(t) has the formv(t ) A cos(ωt )(1.8)dvdt C A ω sin(ωt )(1.9)Then the current i(t) becomesi (t ) Cπ C ω A cos ωt 2 Therefore the current going through a capacitor and the voltage across the capacitor are90 degrees out of phase. It is said that the current leads the voltage by 90 degrees.The general plot of the voltage and current of a capacitor is shown on Figure 4. Thecurrent leads the voltage by 90 degrees.6.071/22.071 Spring 2006, Chaniotakis and Cory3
Figure 4If we take the ratio of the peak voltage to the peak current we obtain the quantityXc 1Cω(1.10)Xc has the units of Volts/Amperes or Ohms and thus it represents some type of resistance.Note that as the frequency ω 0 the quantity Xc goes to infinity which implies that thecapacitor resembles an open circuit .Capacitors do like to pass current at low frequenciesAs the frequency becomes very large ω the quantity Xc goes to zero which impliesthat the capacitor resembles a short circuit.Capacitors like to pass current at high frequenciesCapacitors connected in series and in parallel combine to an equivalent capacitance. Let’sfirst consider the parallel combination of capacitors as shown on Figure 5. Note that allcapacitors have the same voltage, v, across them.i(t)--i1i2i3in v(t)v C1C2C3Cn--Figure 5. Parallel combination of capacitors.6.071/22.071 Spring 2006, Chaniotakis and Cory4
By applying KCL we obtainAnd since ik Cki i1 i 2 i3 in(1.11)dvdvdvdv C 2 C 3 Cndtdtdtdt dv C1 C 2 C 3 Cn Ceq dtdv Ceqdt(1.12)dvwe havedti C1Capacitors connected in parallel combine like resistors in seriesNext let’s look at the series combination of capacitors as shown on Figure 6.C1C2C3 v1 - v2 - v3 -i(t)Cn-- vn -v(t)Figure 6. Series combination of n capacitors.Now by applying KVL around the loop and using Equation (1.7) we havev v1 v 2 v3 vn t111 1i (t )dt v(0) C1 C 2 C 3Cn 0 1 Ceq (1.13)t 1i (t )dt v(0)Ceq 0Capacitors in series combine like resistors in parallel6.071/22.071 Spring 2006, Chaniotakis and Cory5
By extension we can calculate the voltage division rule for capacitors connected in series.Here let’s consider the case of only two capacitors connected in series as shown onFigure 7.i(t) v1-C1 v2-C2v(t)Figure 7. Series combination of two capacitorsThe same current flows through both capacitors and so the voltages v1 and v2 acrossthem are given by:1t1(1.14)v1 idtC1 0tv2 1idtC 2 0(1.15)And KVL around the loop results int1 1v(t ) idt C1 C 2 0Which in turn gives the voltages v1 and v2 in terms of v and the capacitances:C2C1 C 2C1v2 vC1 C 2v1 v(1.16)(1.17)(1.18)Similarly in the parallel arrangement of capacitors (Figure 8) the current division rule is1i1 iC1C1 C 2(1.19)i2 iC2C1 C 2(1.20)Assume here that both capacitors are initially uncharged6.071/22.071 Spring 2006, Chaniotakis and Cory6
i(t) i(t)i1v C1-i2C2Figure 8. Parallel arrangement of two capacitorsThe instantaneous power delivered to a capacitor isP (t ) i (t )v (t )(1.21)The energy stored in a capacitor is the integral of the instantaneous power. Assuming thatthe capacitor had no charge across its plates at t [ v( ) 0] then the energy storedin the capacitor at time t istE (t ) P(τ )dτ t v(τ )i(τ ) dτ tdv(τ ) dτ v(τ )C dτ(1.22) 1 C v(t ) 226.071/22.071 Spring 2006, Chaniotakis and Cory7
Real Capacitors.If the dielectric material between the plates of a capacitor has a finite resistivity – ascompared to infinite resistivity in the case of an ideal capacitor – then there is going to bea small amount of current flowing between the capacitor plates. In addition there are leadresistance and plate effects.In general the circuit model of a non-ideal capacitor is shown on Figure 9 ii Cnon-idealv-CRsRpFigure 9. Circuit of non-ideal capacitorThe resistance Rp is typically very large and it represents the resistance of the dielectricmaterial. Resistance Rs is typically small and it corresponds to the lead and plateresistance as well as resistance effects due to the operating conditions (for example signalfrequency)In practice we are concerned with the in series resistance of a capacitor called theEquivalent Series Resistance (ESR). ESR is a very important capacitor characteristic andmust be taken into consideration in circuit design. Therefore the non-ideal capacitormodel of interest to us is shown oniR(ESR)CFigure 10. Non-ideal capacitor with series resistor.Typical values of ESR are in the mΩ-Ω range.6.071/22.071 Spring 2006, Chaniotakis and Cory8
A capacitor stores energy in the form of an electric fielddv1Current-voltage relationship i C , v idtdtCIn DC the capacitor acts as an open circuitThe capacitance C represents the efficiency of storing charge.The unit of capacitance is the Farad (F). 1 Farad 1Coulomb/1VoltTypical capacitor values are in the mF ( 10 3 F) to pF ( 10 12 F)1The energy stored in a capacitor is E Cv 22Large capacitors should always be stored with shorted leads.Example:A 47µF capacitor is connected to a voltage which varies in time asv (t ) 20 sin(200π t ) volts.Calculate the current i(t) through the capacitori(t) v(t)v-CThe current is given bydvi Cdtd 47 10 6 20sin(200π t ) 47 10 6 20 200π cos(200π t ) 0.59 cos(200π t ) Amperesdt6.071/22.071 Spring 2006, Chaniotakis and Cory9
Example:Calculate the energy stored in the capacitor ofthe circuit to the right under DC conditions.In order to calculate the energy stored in thecapacitor we must determine the voltage acrossit and then use Equation (1.22).1k Ω18 V2k Ω1uFWe know that under DC conditions thecapacitor appears as an open circuit (no currentflowing through it). Therefore the corresponding circuit isv1k Ω2k Ω18 VAnd from the voltage divider formed by the 1kΩ and the 2kΩ resistors the voltage v is12Volts. Therefore the energy stored in the capacitor is11Ec Cv 2 1 10 6 122 72µJoules226.071/22.071 Spring 2006, Chaniotakis and Cory10
ExampleCalculate the energy stored in the capacitors of the following circuit under DCconditions.C150uF10k Ω25k ΩC210 V50k Ω1uFC310uFAgain DC conditions imply that the capacitor behaves like an open circuit and thecorresponding circuit isC1v110k Ω10 V25k Ω50k ΩC2C3v2From this circuit we see that the voltages v1 and v2 are both equal to 10 Volts and thusthe voltage across capacitor C1 is 0 Volts.Therefore the energy stored in the capacitors is:For capacitor C1:For capacitor C2:For capacitor C3:0 Joules11EC 2 C 2v 2 1 10 6 102 50µJoules2211EC 3 C 3v 2 10 10 6 102 500µJoules226.071/22.071 Spring 2006, Chaniotakis and Cory11
InductorsThe inductor is a coil which stores energy in the magnetic fieldConsider a wire of length l forming a loop of area A as shown on Figure 11. A current i(t)is flowing through the wire as indicated. This current generates a magnetic field B whichis equal toB (t ) µi (t )l(1.23)Where µ is the magnetic permeability of the material enclosed by the wire.lLoop lengthi(t)BAAreaFigure 11. Current loop for the calculation of inductanceThe magnetic flux, Φ, through the loop of area A isΦ AB(t )Aµ i (t )l Li (t )(1.24)Aµ.lFrom Maxwell’s equations we know thatWhere we have defined L dΦ v(t )dtd Li (t ) v(t )dt(1.25)(1.26)And by taking L to be a constant we obtain the current-voltage relationship for this loopof wire also called an inductor.6.071/22.071 Spring 2006, Chaniotakis and Cory12
v Ldidt(1.27)The parameter L is called the inductance of the inductor. It has the unit of Henry (H).The circuit symbol and associated electrical variables for the inductor is shown on Figure12iL v Figure 12. Circuit symbol of inductor.di 0 ) the inductor acts as a short circuit (v 0). Also note the inductordtdoes not like current discontinuities since that would require that the voltage across itgoes to infinity which is not physically possible. (We should keep this in mind when wedesign inductive devices. The current through the inductor must not be allowed to changeinstantaneously.)For DC signals (If we integrate Equation (1.27) over time we havett di vdt L dt dt(1.28) ti 1 v dtL (1.29)t1 v dt i (0)L0The constant i(0) represents the current through the inductor at time t 0. (Note that wehave also assumed that the current at t was zero.)6.071/22.071 Spring 2006, Chaniotakis and Cory13
Let’s now consider the circuit shown on Figure 13 where an inductor of inductance L isconnected to a time varying current source i(t).i(t) i(t)vL-Figure 13. Fundamental inductor circuitIf we assume that the current i(t) has the formi (t ) I o cos(ωt )(1.30)didt L I o ω sin(ωt )(1.31)Then the voltage v(t) becomesv(t ) Lπ L ω I o cos ωt 2 Therefore the current going through an inductor and the voltage across the inductor are90 degrees out of phase. Here the voltage leads the current by 90 degrees.The general plot of the voltage and current of an inductor is shown on Figure 14.Figure 146.071/22.071 Spring 2006, Chaniotakis and Cory14
Inductor connected in series and in parallel combine to an equivalent inductance. Let’sfirst consider the parallel combination of inductors as shown on Figure 15. Note that allinductors have the same voltage across them.i(t)--i1i2i3in v(t)vL1L2L3Ln--Figure 15. Parallel combination of inductors.By applying KCL we obtaini i1 i 2 i3 in(1.32)tAnd since ik 1vdt ik (0) we haveLk 0ti ttt1111vdt i1(0) vdt i 2(0) vdt i3(0) vdt in(0) L1 0L2 0L3 0Ln 0 t111 1vdt i1(0) i 2(0) i3(0) in(0) L1 L 2 L3Ln 0i (0) 1 Leq (1.33)t 1vdt i (0)Leq 0Inductors in parallel combine like resistors in parallelNext let’s look at the series combination of inductors as shown on Figure 16.i(t)L1L2L3 v1 - v2 - v3 ----Ln vn -v(t)Figure 16. Series combination of inductors.6.071/22.071 Spring 2006, Chaniotakis and Cory15
Now by applying KVL around the loop we havev v1 v 2 v3 vn di L1 L 2 L3 Ln dtLeq di Leqdt(1.34)Inductor in series combine like resistor in seriesThe energy stored in an inductor is the integral of the instantaneous power delivered tothe inductor. Assuming that the inductor had no current flowing through it att [i ( ) 0] then the energy stored in the inductor at time t istE (t ) P(τ )dτ t v(τ )i(τ ) dτ tdi (τ ) i (τ )dτ L dτ(1.35) 1L i (t ) 226.071/22.071 Spring 2006, Chaniotakis and Cory16
Real Inductors.There are two contributions to the non-ideal behavior of inductors.1. The finite resistance of the wire used to wind the coil2. The cross turn effects which become important at high frequenciesThe non-ideal inductor may thus be modeled as shown on Figure 17 i L v- resistance of coil(small value)iRcvLRf-Frequency dependentturn to turnfield effects(important at highfrequecnies)non-idealFigure 17. Circuit momdel of non-ideal inductorIn addition to the resistive non-idealities of inductors there could also be capacitiveeffects. These effects usually become important at high frequencies. Unless statedotherwise, these effects will be neglected in out analysis.A inductor stores energy in a magnetic fielddi1Current-voltage relationship v L , i vdtdtL1The energy stored in an inductor is E Li 22In DC the inductor behaves like a short circuitThe inductance L represents the efficiency of storing magnetic flux.6.071/22.071 Spring 2006, Chaniotakis and Cory17
Problems:Calculate the equivalent capacitance for the following arrangements:1F5FCeq100 F2F1FCC2CCeqC2CC---2Cto infinity---Calculate the voltage across each capacitor and the energy stored in each capacitor.10 V2uF10uF10uF20uF5uFIn the circuit below the current source provides a current of i 10 exp( 2t ) mA. Calculatethe voltage across each capacitor and the energy stored in each capacitor at time t 2 sec. i(t)v1 10uF20uF v2-5uF6.071/22.071 Spring 2006, Chaniotakis and Cory18
6.071/22.071 Spring 2006, Chaniotakis and Cory19
Capacitors connected in parallel combine like resistors in series Next let’s look at the series combination of capacitors as shown on Figure 6. i(t) v(t) C1 C2 C3 Cn - - - v1 - v2 - v3 - vn - Figure 6. Series combination of n capacitors. Now by applying KVL around the loop and usi
Inductors in Series – No Mutual inductance When inductors are connected in series, the total inductance is the sum of the individual inductors' inductances. L T L 1 L 2 L N Example #1 Three inductors of 10mH, 40mH and 50mH are connected together in a series
SMD Inductors Series All specification & dimensions are subject to change,please call your nearest KLS sales represesntative for update information ORDER INFORMATION Product NO.: KLS1 - -2218 SP32 K-R Inductors SMD INDUCTORS Series Electrical code 1.0 220:.μH Tolerance:K 10%,M 20%. KLS18-SP32 SMD
Mutually coupled inductors in series Consider there are two inductors L1 and L2 in series, which are magnetically coupled and have a mutual inductance M. The magnetic field of the two inductors could be aiding or opposing each other, depending on their orientation (fig 6.1). a) b) Fig. 6.1. Mutually cou
Inductors LL and LS have been implemented as bond wire inductors. In this design we have modeled bond wire inductors with an inductance of 1 nH/mm, a series resistance of 0.5 Ω/mm, and we have also accounted for pad capacitances of 100 fF at each bond pad. Bond wire inductors are a
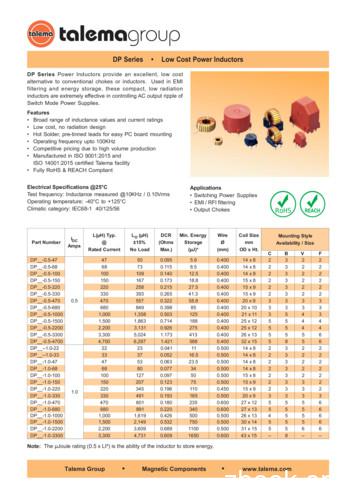
DP Series Power Inductors provide an excellent, low cost alternative to conventional chokes or inductors. Used in EMI filtering and energy storage, these compact, low radiation inductors a
Inductors in series add like resistors in series. Note the total inductance is greater than the individual inductances. Two inductors in parallel: I V I1 L1 I2 L2 Since the inductors are in
SMD Inductors Metal Composite Power Inductors MPXV Automotive Grade Part Number System MPX 1 D0520 L 1R5 Series Version Size Code Inductor Inductance Code µH MPXV 1 D0520 5x5x2.0 mm D0530 5x5x3.0 mm D0618 6x6x1.8 mm D0624 6x6x2.4 mm D0630 6x6x3.0 mm D0650 6x6x5.0 mm D
2.3.1 Series Inductors Inductors connected in series are connected along a single path, so the same current flows through all of the components. Figure 2.5 is the connection for series inductors. Total inductance (L T) for a series circuit is the sum of all values of inductance in the circuit. L1 L