Jeffrey R. Chasnov - Department Of Mathematics, HKUST
Matrix Algebra for EngineersLecture Notes forJeffrey R. Chasnov
The Hong Kong University of Science and TechnologyDepartment of MathematicsClear Water Bay, KowloonHong Kongc 2018, 2019 by Jeffrey Robert ChasnovCopyright This work is licensed under the Creative Commons Attribution 3.0 Hong Kong License. To view a copy of thislicense, visit http://creativecommons.org/licenses/by/3.0/hk/ or send a letter to Creative Commons, 171 SecondStreet, Suite 300, San Francisco, California, 94105, USA.
PrefaceView the promotional video on YouTubeThese are my lecture notes for my online Coursera course, Matrix Algebra for Engineers. I havedivided these notes into chapters called Lectures, with each Lecture corresponding to a video onCoursera. I have also uploaded all my Coursera videos to YouTube, and links are placed at the top ofeach Lecture.There are problems at the end of each lecture chapter and I have tried to choose problems thatexemplify the main idea of the lecture. Students taking a formal university course in matrix or linearalgebra will usually be assigned many more additional problems, but here I follow the philosophythat less is more. I give enough problems for students to solidify their understanding of the material,but not too many problems that students feel overwhelmed and drop out. I do encourage students toattempt the given problems, but if they get stuck, full solutions can be found in the Appendix.There are also additional problems at the end of coherent sections that are given as practice quizzeson the Coursera platform. Again, students should attempt these quizzes on the platform, but if astudent has trouble obtaining a correct answer, full solutions are also found in the Appendix.The mathematics in this matrix algebra course is at the level of an advanced high school student, buttypically students would take this course after completing a university-level single variable calculuscourse. There are no derivatives and integrals in this course, but student’s are expected to have acertain level of mathematical maturity. Nevertheless, anyone who wants to learn the basics of matrixalgebra is welcome to join.Jeffrey R. ChasnovHong KongJuly 2018
iv
ContentsIMatrices11Definition of a matrix52Addition and multiplication of matrices73Special matrices9Practice quiz: Matrix definitions114Transpose matrix135Inner and outer products156Inverse matrix17Practice quiz: Transpose and inverses197Orthogonal matrices218Rotation matrices239Permutation matrices25Practice quiz: Orthogonal matrices27IISystems of Linear Equations2910 Gaussian elimination3311 Reduced row echelon form3712 Computing inverses39Practice quiz: Gaussian elimination4113 Elementary matrices4314 LU decomposition45v
CONTENTSvi15 Solving (LU)x bPractice quiz: LU decompositionIIIVector Spaces47515316 Vector spaces5717 Linear independence5918 Span, basis and dimension61Practice quiz: Vector space definitions6319 Gram-Schmidt process6520 Gram-Schmidt process example67Practice quiz: Gram-Schmidt process6921 Null space7122 Application of the null space7523 Column space7724 Row space, left null space and rank79Practice quiz: Fundamental subspaces8125 Orthogonal projections8326 The least-squares problem8527 Solution of the least-squares problem87Practice quiz: Orthogonal projections91Eigenvalues and Eigenvectors9328 Two-by-two and three-by-three determinants9729 Laplace expansion99IV30 Leibniz formula10331 Properties of a determinant105Practice quiz: Determinants10732 The eigenvalue problem10933 Finding eigenvalues and eigenvectors (1)111
CONTENTSvii34 Finding eigenvalues and eigenvectors (2)113Practice quiz: The eigenvalue problem11535 Matrix diagonalization11736 Matrix diagonalization example11937 Powers of a matrix12138 Powers of a matrix example123Practice quiz: Matrix diagonalizationAppendixA Problem and practice quiz solutions125127129
viiiCONTENTS
Week IMatrices1
3In this week’s lectures, we learn about matrices. Matrices are rectangular arrays of numbers orother mathematical objects and are fundamental to engineering mathematics. We will define matricesand how to add and multiply them, discuss some special matrices such as the identity and zero matrix,learn about transposes and inverses, and define orthogonal and permutation matrices.
4
Lecture 1Definition of a matrixView this lecture on YouTubeAn m-by-n matrix is a rectangular array of numbers (or other mathematical objects) with m rowsand n columns. For example, a two-by-two matrix A, with two rows and two columns, looks likeA abcd!.The first row has elements a and b, the second row has elements c and d. The first column has elementsa and c; the second column has elements b and d. As further examples, two-by-three and three-by-twomatrices look likeB abcdef !,a C bcd e .fOf special importance are column matrices and row matrices. These matrices are also called vectors.The column vector is in general n-by-one and the row vector is one-by-n. For example, when n 3,we would write a column vector as a x b ,cand a row vector as y ab c .A useful notation for writing a general m-by-n matrix A is a1na22.······.am2···amna11a12 a21A . .am1 a2n . . Here, the matrix element of A in the ith row and the jth column is denoted as aij .5
LECTURE 1. DEFINITION OF A MATRIX6Problems for Lecture 11. The diagonal of a matrix A are the entries aij where i j.a) Write down the three-by-three matrix with ones on the diagonal and zeros elsewhere.b) Write down the three-by-four matrix with ones on the diagonal and zeros elsewhere.c) Write down the four-by-three matrix with ones on the diagonal and zeros elsewhere.Solutions to the Problems
Lecture 2Addition and multiplication ofmatricesView this lecture on YouTubeMatrices can be added only if they have the same dimension. Addition proceeds element by element.For example,abcd! efgh! a eb fc gd h!.Matrices can also be multiplied by a scalar. The rule is to just multiply every element of the matrix.For example,kabcd! kakbkckd!.Matrices (other than the scalar) can be multiplied only if the number of columns of the left matrixequals the number of rows of the right matrix. In other words, an m-by-n matrix on the left can onlybe multiplied by an n-by-k matrix on the right. The resulting matrix will be m-by-k. Evidently, matrixmultiplication is generally not commutative. We illustrate multiplication using two 2-by-2 matrices:abcd!efgh! ae bga f bhce dgc f dh!,efgh!abcd! ae c fbe d fag chbg dh!.First, the first row of the left matrix is multiplied against and summed with the first column of the rightmatrix to obtain the element in the first row and first column of the product matrix. Second, the firstrow is multiplied against and summed with the second column. Third, the second row is multipliedagainst and summed with the first column. And fourth, the second row is multiplied against andsummed with the second column.In general, an element in the resulting product matrix, say in row i and column j, is obtained bymultiplying and summing the elements in row i of the left matrix with the elements in column j ofthe right matrix. We can formally write matrix multiplication in terms of the matrix elements. Let Abe an m-by-n matrix with matrix elements aij and let B be an n-by-p matrix with matrix elements bij .Then C AB is an m-by-p matrix, and its ij matrix element can be written asncij aik bkj .k 1Notice that the second index of a and the first index of b are summed over.7
LECTURE 2. ADDITION AND MULTIPLICATION OF MATRICES8Problems for Lecture 21. Define the matricesA ! 1, B 1 1121D 212 4 2!3 4, E 4 34!C ,11221!,!2.Compute if defined: B 2A, 3C E, AC, CD, CB.!!!1 22 14 32. Let A ,B and C . Verify that AB AC and yet B ̸ C.2 41 30 2 111200 3. Let A 112 3 and D 0043 0 . Compute AD and DA.0434. Prove the associative law for matrix multiplication. That is, let A be an m-by-n matrix, B an n-by-pmatrix, and C a p-by-q matrix. Then prove that A(BC) (AB)C.Solutions to the Problems
Lecture 3Special matricesView this lecture on YouTubeThe zero matrix, denoted by 0, can be any size and is a matrix consisting of all zero elements. Multiplication by a zero matrix results in a zero matrix. The identity matrix, denoted by I, is a square matrix(number of rows equals number of columns) with ones down the main diagonal. If A and I are thesame sized square matrices, thenAI IA A,and multiplication by the identity matrix leaves the matrix unchanged. The zero and identity matricesplay the role of the numbers zero and one in matrix multiplication. For example, the two-by-two zeroand identity matrices are given by0 0000!I ,1001!.A diagonal matrix has its only nonzero elements on the diagonal. For example, a two-by-two diagonalmatrix is given byD d100d2!.Usually, diagonal matrices refer to square matrices, but they can also be rectangular.A band (or banded) matrix has nonzero elements only on diagonal bands. For example, a three-bythree band matrix with nonzero diagonals one above and one below a nonzero main diagonal (calleda tridiagonal matrix) is given by d1a10 B b10d2 a2 .b2d3An upper or lower triangular matrix is a square matrix that has zero elements below or above thediagonal. For example, three-by-three upper and lower triangular matrices are given by abc U 00d e ,0f 9 a00 L bcd 0 .ef
LECTURE 3. SPECIAL MATRICES10Problems for Lecture 31. Let! 12.4 8A Construct a two-by-two matrix B such that AB is the zero matrix. Use two different nonzero columnsfor B.2. Verify thata100a2!b100b2! a1 b100a2 b2!.Prove in general that the product of two diagonal matrices is a diagonal matrix, with elements givenby the product of the diagonal elements.3. Verify thata1a20a3!b1b20b3! a1 b1a1 b2 a2 b30a3 b3!.Prove in general that the product of two upper triangular matrices is an upper triangular matrix, withthe diagonal elements of the product given by the product of the diagonal elements.Solutions to the Problems
Practice quiz: Matrix definitions1. Identify the two-by-two matrix with matrix elements aij i j.!10a)0 1! 1 0b)0 1!0 1c) 1 0!0 1d)10!!1 1 112. The matrix productis equal to 111 1! 22a)2 2!2 2b) 22! 2 2c) 2 2! 2 2d)22n3. Let A and B be n-by-n matrices with (AB)ij k 1then aik 0 or bkj 0 whenA. k iB. k i aik bkj .C. k jD. k ja) A and C onlyb) A and D onlyc) B and C onlyd) B and D onlySolutions to the Practice quiz11If A and B are upper triangular matrices,
12LECTURE 3. SPECIAL MATRICES
Lecture 4Transpose matrixView this lecture on YouTubeThe transpose of a matrix A, denoted by AT and spoken as A-transpose, switches the rows andcolumns of A. That is, a1na22.······.am2···amna11a12 a21if A . .am1 a2n . ,. am1a22.······.a2n···amna11a21 a12then A . .a1nT am2 . . In other words, we writeaTij a ji .Evidently, if A is m-by-n then AT is n-by-m. As a simple example, view the following transpose pair: a bcd T e fabcdef!.The following are useful and easy to prove facts: AT T A, and (A B)T AT BT .A less obvious fact is that the transpose of the product of matrices is equal to the product of thetransposes with the order of multiplication reversed, i.e.,(AB)T BT AT .If A is a square matrix, and AT A, then we say that A is symmetric. If AT A, then we say that Ais skew symmetric. For example, three-by-three symmetric and skew symmetric matrices look like abc bcd e ,ef 0bc b c0 e . e0Notice that the diagonal elements of a skew-symmetric matrix must be zero.13
14LECTURE 4. TRANSPOSE MATRIXProblems for Lecture 41. Prove that (AB)T BT AT .2. Show using the transpose operator that any square matrix A can be written as the sum of a symmetric and a skew-symmetric matrix.3. Prove that AT A is symmetric.Solutions to the Problems
Lecture 5Inner and outer productsView this lecture on YouTubeThe inner product (or dot product or scalar product) between two vectors is obtained from the matrix product of a row vector times a column vector. A row vector can be obtained from a columnvector by the transpose operator. With the 3-by-1 column vectors u and v, their inner product is givenby uT v u1u2u3 v1 v2 u1 v1 u2 v2 u3 v3 .v3If the inner product between two nonzero vectors is zero, we say that the vectors are orthogonal. Thenorm of a vector is defined by 1/2 1/2 u uT u u21 u22 u23.If the norm of a vector is equal to one, we say that the vector is normalized. If a set of vectors aremutually orthogonal and normalized, we say that these vectors are orthonormal.An outer product is also defined, and is used in some applications. The outer product between uand v is given by u1 uvT u2 v1u3v2 u1 v1u1 v2u1 v3 v3 u2 v1u3 v1u2 v2 u2 v3 .u3 v2u3 v3 Notice that every column is a multiple of the single vector u, and every row is a multiple of the singlevector vT .15
LECTURE 5. INNER AND OUTER PRODUCTS16Problems for Lecture 5 ad 1. Let A be a rectangular matrix given by A b e . Compute AT A and show that it is a symmetricc fsquare matrix and that the sum of its diagonal elements is the sum of the squares of all the elementsof A.2. The trace of a square matrix B, denoted as Tr B, is the sum of the diagonal elements of B. Prove thatTr(AT A) is the sum of the squares of all the elements of A.Solutions to the Problems
Lecture 6Inverse matrixView this lecture on YouTubeSquare matrices may have inverses. When a matrix A has an inverse, we say it is invertible anddenote its inverse by A 1 . The inverse matrix satisfiesAA 1 A 1 A I.If A and B are invertible matrices, then (AB) 1 B 1 A 1 . Furthermore, if A is invertible then so isAT , and (AT ) 1 (A 1 )T .It is illuminating to derive the inverse of a general 2-by-2 matrix. Writeabcd!x1x2y1y2! 1001!,and try to solve for x1 , y1 , x2 and y2 in terms of a, b, c, and d. There are two inhomogeneous and twohomogeneous linear equations:ax1 by1 1,cx1 dy1 0,cx2 dy2 1,ax2 by2 0.To solve, we can eliminate y1 and y2 using the two homogeneous equations, and find x1 and x2 usingthe two inhomogeneous equations. The solution for the inverse matrix is found to beabcd! 11 ad bcd c! b.aThe term ad bc is just the definition of the determinant of the two-by-two matrix:detabcd! ad bc.The determinant of a two-by-two matrix is the product of the diagonals minus the product of theoff-diagonals. Evidently, a two-by-two matrix A is invertible only if det A ̸ 0. Notice that the inverseof a two-by-two matrix, in words, is found by switching the diagonal elements of the matrix, negatingthe off-diagonal elements, and dividing by the determinant.Later, we will show that an n-by-n matrix is invertible if and only if its determinant is nonzero.This will require a more general definition of the determinant.17
LECTURE 6. INVERSE MATRIX18Problems for Lecture 61. Find the inverses of the matrices5645!and6433!.2. Prove that if A and B are same-sized invertible matrices , then (AB) 1 B 1 A 1 .3. Prove that if A is invertible then so is AT , and (AT ) 1 (A 1 )T .4. Prove that if a matrix is invertible, then its inverse is unique.Solutions to the Problems
Practice quiz: Transpose and inverses1. (ABC)T is equal toa) AT BT CTb) AT CT BTc) CT AT BTd) CT BT AT2. Suppose A is a square matrix. Which matrix is not symmetric?a) A ATb) AATc) A ATd) AT A3. Which matrix is the inverse of1a)2 2 12!1b)2 221 2!2221c)2 1 21d)2 2 2122212!?!!Solutions to the Practice quiz19
20LECTURE 6. INVERSE MATRIX
Lecture 7Orthogonal matricesView this lecture on YouTubeA square matrix Q with real entries that satisfiesQ 1 QTis called an orthogonal matrix. Another way to write this definition isQQT IQT Q I.andWe can more easily understand orthogonal matrices by examining a general two-by-two example. LetQ be the orthogonal matrix given byQ q11q12q21q22! q1 q2 ,where q1 and q2 are the two-by-one column vectors of the matrix Q. ThenQT Q qT1qT2! q1 q2 qT1 q1qT1 q2qT2 q1qT2 q2!.If Q is orthogonal, then QT Q I andqT1 q1 qT2 q2 1andqT1 q2 qT2 q1 0.That is, the columns of Q form an orthonormal set of vectors. The same argument can also be madefor the rows of Q.Therefore, an equivalent definition of an orthogonal matrix is a square matrix with real entrieswhose columns (and also rows) form a set of orthonormal vectors.There is a third equivalent definition of an orthogonal matrix. Let Q be an n-by-n orthogonalmatrix, and let x be an n-by-one column vector. Then the length squared of the vector Qx is given by Qx 2 (Qx)T (Qx) xT QT Qx xT Ix xT x x 2 .The length of Qx is therefore equal to the length of x, and we say that an orthogonal matrix is a matrixthat preserves lengths. In the next lecture, an example of an orthogonal matrix will be the matrix thatrotates a two-dimensional vector in the plane.21
22LECTURE 7. ORTHOGONAL MATRICESProblems for Lecture 71. Show that the product of two orthogonal matrices is orthogonal.2. Show that the n-by-n identity matrix is orthogonal.Solutions to the Problems
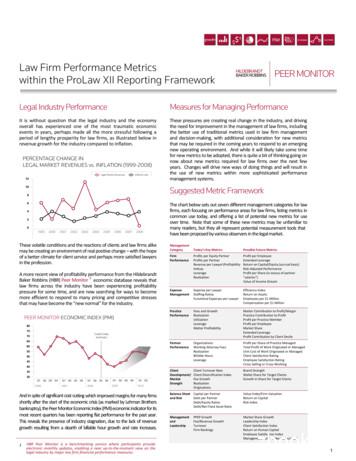
Lecture 8Rotation matricesView this lecture on YouTubeA matrix that rotates a vector in space doesn’t change the vector’s length and so should be an orthog-y'yrrθψx'xRotating a vector in the x-y plane.onal matrix. Consider the two-by-two rotation matrix that rotates a vector through an angle θ in thex-y plane, shown above. Trigonometry and the addition formula for cosine and sine results inx ′ r cos (θ ψ)y′ r sin (θ ψ) r (cos θ cos ψ sin θ sin ψ) r (sin θ cos ψ cos θ sin ψ) x cos θ y sin θ x sin θ y cos θ.Writing the equations for x ′ and y′ in matrix form, we havex′y′! cos θsin θ sin θcos θ!xy!.The above two-by-two matrix is a rotation matrix and we will denote it by Rθ . Observe that the rowsand columns of Rθ are orthonormal and that the inverse of Rθ is just its transpose. The inverse of Rθrotates a vector by θ.23
LECTURE 8. ROTATION MATRICES24Problems for Lecture 81. Let R(θ ) cos θsin θ! sin θ. Show that R( θ ) R(θ ) 1 .cos θ2. Find the three-by-three matrix that rotates a three-dimensional vector an angle θ counterclockwisearound the z-axis.Solutions to the Problems
Lecture 9Permutation matricesView this lecture on YouTubeAnother type of orthogonal matrix is a permutation matrix. A permutation matrix, when multiplyingon the left, permutes the rows of a matrix, and when multiplying on the right, permutes the columns.Clearly, permuting the rows of a column vector will not change its length.For example, let the string {1, 2} represent the order of the rows of a two-by-two matrix. Thenthe two possible permutations of the rows are given by {1, 2} and {2, 1}. The first permutation isno permutation at all, and the corresponding permutation matrix is simply the identity matrix. Thesecond permutation of the rows is achieved by0110!abcd! cdab!.The rows of a three-by-three matrix have 3! 6 possible permutations, namely {1, 2, 3}, {1, 3, 2},{2, 1, 3}, {2, 3, 1}, {3, 1, 2}, {3, 2, 1}. For example, the row permutation {3, 1, 2} is achieved by 001abcghi 100 0 deb c .10gh f aidefNotice that the permutation matrix is obtained by permuting the corresponding rows of the identitymatrix, with the rows of the identity matrix permuted as {1, 2, 3} {3, 1, 2}. That a permutationmatrix is just a row-permuted identity matix is made evident by writingPA (PI)A,where P is a permutation matrix and PI is the identity matrix with permuted rows. The identity matrixis orthogonal, and so is the permutation matrix obtained by permuting the rows of the identity matrix.25
26LECTURE 9. PERMUTATION MATRICESProblems for Lecture 91. Write down the six three-by-three permutation matrices corresponding to the permutations {1, 2, 3},{1, 3, 2}, {2, 1, 3}, {2, 3, 1}, {3, 1, 2}, {3, 2, 1}.2. Find the inverses of all the three-by-three
In this week’s lectures, we learn about matrices. Matrices are rectangular arrays of numbers or other mathematical objects and are fundamental to engineering mathematics. We will define matrices and how to add and multiply them, discuss some special matrices such as the identity and zero matrix,
Matrix Algebra for Engineers If you want to learn vector calculus (also known as multivariable calculus, or calcu-lus three), you can sign up for Vector Calculus for Engineers And if your interest is numerical methods, have a go at Numerical Methods for Engineers Jeffrey R. Chasnov Hong Kong February 2021 iii
There are some problems at the end of each lecture chapter. These problems are designed to exemplify the main ideas of the lecture. Students taking a formal university course in multivariable calculus will usually be assigned many more problems, some of them quite diffi
Jeffrey resigned his part-time position with the bank, bought out the minority shareholders, including Sessions and Lechner, increased his own salary to 5,000 per year, and changed the firm’s name to The Jeffrey Manufacturing Co. A year later, the business moved to this First Avenue site. Jeffrey’s Manufacturing History in Columbus Page 4
14. Upon infonnation and belief, Respondent Jeffrey B. Lackey ("Jeffrey") is a citizen and resident of Dorchester County, South Carolina, residing at 8 871 East Fairway Woods Drive, North Charleston, South Carolina 29420. 15. Jeffrey was a licensee of the Division, having been granted Tennessee insurance
Jeffrey Blecharczyk Sent via e-mail to: Jeffrey.Blecharczyk@des.nh.gov Land Resources Management Program . Department of Environmental Services . 29 Hazen Drive, PO Box 95 . Concord, NH 03302-0095 . Mr. Blecharczyk: This letter has been prepared on behalf of Antrim Wind Energy LLC (Antrim Wind) in response to your
Curriculum vitae - Jeffrey B. Kaplan 12/31/20 2 Awards Year(s) Award or position 1983 Recipient, University of Illinois Graduate Fellowship 1985-1986 Recipient, NIH National Research Service Award Fellowship 1987 Invited Participant, UCLA International School on Molecular Evolution 2008 Recipient, Top 10 Scientist Award, New Jersey Business Magazine
Scott Jeffrey University of Chicago Graduate School of Business 1101 E. 58th Street Chicago, IL 60637 (773) 702-0537 email: scott.jeffrey@gsb.uchicago.edu
ASTM C 1628 06ASTM C 1628 06 Standard Specification for Joints for Concrete Gravity Flow Sewer Pipe Using Rubber Gaskets AS C 16 09ASTM C 1677 09 Standard Specification for Joints for Concrete Box, Using Rubber Gaskets ASTM C 1619 05 Standard Specification for Elastomeric Seals for Joining Concrete Structures ASTM C 505 05a Standard Specification for Irrigation Pipe with Rubber Gasket Joints .