Brain Networks And Topology
Brain Networks and TopologyMatilde Marcolli and Doris TsaoMa191b Winter 2017Geometry of NeuroscienceMatilde Marcolli and Doris TsaoBrain Networks
References for this lecture:Alex Fornito, Andrew Zalesky, Edward Bullmore,Fundamentals of Brain Network Analysis, Elsevier, 2016Olaf Sporns, Networks of the Brain, MIT Press, 2010Olaf Sporns, Discovering the Human Connectome, MIT Press,2012Fan Chung, Linyuan Lu, Complex Graphs and Networks,American Mathematical Society, 2004László Lovász, Large Networks and Graph Limits, AmericanMathematical Society, 2012Matilde Marcolli and Doris TsaoBrain Networks
Graphs G (V , E , ) V V (G ) set of vertices (nodes) E E (G ) set of edges (connections) boundary map : E (G ) V (G ) V (G ), boundary vertices (e) {v , v 0 } directed graph (oriented edges): source and target mapss : E (G ) V (G ),t : E (G ) V (G ), (e) {s(e), t(e)} looping edge: s(e) t(e) starts and ends at same vertex;parallel edges: e 6 e 0 with (e) (e 0 ) simplifying assumption: graphs G with no parallel edges and nolooping edges (sometimes assume one or the other) additional data: label functions fV : V (G ) LV andfE : E (G ) LE to sets of vertex and edge labels LV and LEMatilde Marcolli and Doris TsaoBrain Networks
Examples of GraphsMatilde Marcolli and Doris TsaoBrain Networks
Network Graphs(Example from Facebook)Matilde Marcolli and Doris TsaoBrain Networks
Increasing Randomnessrewiring probability pwith probability p edges are disconnected and attached to a randomlychosen other vertex (Watts and Strogatz 1998)Matilde Marcolli and Doris TsaoBrain Networks
Brain Networks: Macroscopic Scale (brain areas)Matilde Marcolli and Doris TsaoBrain Networks
Brain Networks: Macroscopic Scale (brain areas)Matilde Marcolli and Doris TsaoBrain Networks
Brain Networks: Microscopic Scale (individual neurons)(Clay Reid, Allen Institute; Wei-Chung Lee, Harvard Medical School;Sam Ingersoll, graphic artist; largest mapped network of individualcortical neurons, 2016)Matilde Marcolli and Doris TsaoBrain Networks
Modeling Brain Networks with Graphs1Spatial embeddings (embedded graphs G S 3 , knotting andlinking, topological invariants of embedded graphs)2Vertex labels (heterogeneity of node types): distinguishdifferent kinds of neurons/different areas3Edge labels (heterogeneity of edge types)4Orientations (directionality of connections): directed graphs5Weights (connection strengths)6Dynamical changes of network topologyMatilde Marcolli and Doris TsaoBrain Networks
Connectivity and Adjacency Matrix connectivity matrix C (Cij ) matrix size N N withN #V (G ), with Cij R connectivity strength for oriented edgefrom vi to vj sign of Cij : excitatory/inhibitory connection Cij 0 no oriented connecting edges between these vertices in general Cij 6 Cji for directed graphs, while Cij Cji fornon-oriented can use Cij Z for counting multiple parallel edges Cii 0 if no looping edges adjacency matrix A (Aij ) also N N with Aij 1 if there is(at least) an edge from vi to vj and zero otherwise Aij 1 if Cij 6 0 and Aij 0 if Cij 0 if no parallel (oriented) edges: can reconstruct G from A (Aij )matrixMatilde Marcolli and Doris TsaoBrain Networks
Connectivity and Adjacency MatrixMatilde Marcolli and Doris TsaoBrain Networks
Filtering the Connectivity Matrixvarious methods, for example pruning weaker connections:thresholdMatilde Marcolli and Doris TsaoBrain Networks
connection densityPijκ AijN(N 1)density of edges over choices of pairs of verticesP total weight W 12 ij wij (for instance strength ofconnection positive/negative Cij ) how connectivity varies across nodes: valence of vertices (nodedegree), distribution of values of vertex valence over graph (e.g.most vertices with few connections, a few hubs with manyconnections: airplane travel, math collaborations) in/out degree ι(v ) #{e : v (e)} vertex valence; fororiented graph in-degree ι (v ) #{e : t(e) v } and out-degreeι (v ) #{e : s(e) v }XXι (v )#E ι (v ) v mean in/outP degreehι i N1 v ι (v ) #EN v1NPMatilde Marcolli and Doris Tsaovι (v ) hι iBrain Networks
Degree Distribution P(deg(v ) k) fraction of vertices (nodes) of valence (degree) kErdös–Rényi graphs: generate random graphs by connectingvertices randomly with equal probability p: all graphs with Nvertices and M edges have equal probabilityNp M (1 p)( 2 ) M for Erdös–Rényi graphs degree distribution N 1 kP(deg(v ) k) p (1 p)N 1 kksecond exponent N 1 k remaining possible connection from achosen vertex (no looping edges) after removing a choice of kedges p connection density of the graph (network)Matilde Marcolli and Doris TsaoBrain Networks
An Erdös–Rényi graph generated with p 0.001Matilde Marcolli and Doris TsaoBrain Networks
the Erdös–Rényi degree distribution satisfies for n N 1 k(np)k e npP(deg(v ) k) p (1 p)N 1 k k!k so for large n the distribution is PoissonP(k) λk e λk! . but Erdös–Rényi graphs not a good model for brain networksMatilde Marcolli and Doris TsaoBrain Networks
Scale-free networks . power lawsP(deg(v ) k) k γfor some γ 0 slower decay rate than in binomial case: fat tail . higherprobability than in Erdös–Rényi case of highly connected large knodes Erdös–Rényi case has a peak in the distribution: a characteristicscale of the network power law distribution has no peak: no characteristic scale.scale free (typical behavior of self-similar and fractal systems)Matilde Marcolli and Doris TsaoBrain Networks
Poisson versus Power Law degree distributions(nodes vertices, links edges, number of links valence)Matilde Marcolli and Doris TsaoBrain Networks
Matilde Marcolli and Doris TsaoBrain Networks
Broad Scale Networks intermediate class: more realistic to model brain networks exponentially truncated power lawP(deg(v ) k) k γ e k/kc cutoff degree kc : for small kc quicker transition to anexponential distribution range of scales over which power law behavior is dominant so far measurements of human and animal brain networksconsistent with scale free and broad scale networksMatilde Marcolli and Doris TsaoBrain Networks
For weighted vertices with weights w R weight distribution: best fitting for brain networks log-normaldistribution (log w µ)21 expP(weight(v ) w ) 2σ 2w σ 2πGaussian in log coordimates why log-normal? model based on properties:1geometry of embedded graph with distribution of interregionaldistances Gaussian2distance dependent cost of long distance connectionsdrop in probability of long distance connections with strong weightsMatilde Marcolli and Doris TsaoBrain Networks
Centrality a node is more “central” to a network the moreit is highly connected (large valence) – degreeit is located on the shortest path between other nodes –betweennessit is close to a large number of other nodes (eg via highlyconnected neighbors) – closeness valence deg(v ) is a measure of centrality (but not so goodbecause it does not distinguish between highly or sparselyconnected neighbors)Matilde Marcolli and Doris TsaoBrain Networks
Matilde Marcolli and Doris TsaoBrain Networks
Perron–Frobenius centrality Perron–Frobenius theorem (version for non-negative matrices)A (Aij ) non-negative N N matrix: Aij 0, i, jA is primitive if k N such that Ak is positiveA irreducible iff i, j, k N such that Akij 0 (implies I Aprimitive)Directed graph GA with N vertices and edge from vi to vj iffAij 0: matrix A irreducible iff GA strongly connected (everyvertex is reachable through an oriented path from every othervertex)Period hA : greatest common divisor of lengths of all closeddirected paths in GAMatilde Marcolli and Doris TsaoBrain Networks
Assume A non-negative and irreducible with period hA and spectralradius ρA , then:1ρA 0 and eigenvalue of A (Perron–Frobenius eigenvalue);simple2Left eigenvector VA and right eigenvector WA with all positivecomponents (Perron–Frobenius eigenvector): onlyeigenvectors with all positive components3hA complex eigenvectors with eigenvalues on circle λ ρA4spectrum invariant under multiplication by e 2πi/hATake A adjacency matrix of graph GMatilde Marcolli and Doris TsaoBrain Networks
A adjacency matrix of graph G vertex v vi : PF centralityCPF (vi ) VA,i 1 XAij VA,jρAjith component of PF eigenvector VA high centrality if high degree (many neighbors), neighbors ofhigh degree, or both can use VA or WA , left/right PF eigenvectors: centralityaccording to in-degree or out-degreeMatilde Marcolli and Doris TsaoBrain Networks
Page Rank Centrality (google) D diagonal matrix Dii max{deg(vi )out , 1} α, β adjustable parametersCPR (vi ) ((I αAD 1 ) 1 β1)iwith 1 vector of N entries 1 this scales contributions of neighbors of node vi by their degree:dampens potential bias of nodes connected to nodes of high degreeMatilde Marcolli and Doris TsaoBrain Networks
Delta Centrality measure of how much a topological property of the graphchanges if a vertex is removed graph G and vertex v V (G ): remove v and star S(v ) of edgesadjacent to vGv G r S(v ) topological invariants of (embedded) graph M(G ) (with integeror real values) delta centrality with respect to MCM (v ) M(G ) M(Gv )M(G )Matilde Marcolli and Doris TsaoBrain Networks
(A) betweenness; (B) closeness; (C) eigenvector (PF); (D) degreeMatilde Marcolli and Doris TsaoBrain Networks
Matilde Marcolli and Doris TsaoBrain Networks
Eigenvalue and PageRank centrality in brain networksX.N.Zuo, R.Ehmke, M.Mennes, D.Imperati, F.X.Castellanos, O.Sporns,M.P.Milham, Network Centrality in the Human Functional Connectome,Cereb Cortex (2012) 22 (8): 1862-1875.Matilde Marcolli and Doris TsaoBrain Networks
Connected Components what is the right notion of “connectedness” for a large graph?small components breaking off should not matter, but largecomponents becoming separated should is there one large component? Erdös–Rényi graphs: size of largest component (N #V (G ))sharp increase at p 1/Ngraph tends to be connected for p log NNfor p N1 fragmented graph: many connected components ofcomparable (small) sizefor N1 p logNN emergence of one giant component; othercomponents still exist of smaller sizeMatilde Marcolli and Doris TsaoBrain Networks
(from Daron Acemoglu and Asu Ozdaglar, Lecture Notes on Networks)Matilde Marcolli and Doris TsaoBrain Networks
How to prove the emergence of connectedness?(Argument from Daron Acemoglu and Asu Ozdaglar, LectureNotes on Networks) threshold function τ (N) for a property P(G ) of a random graphG with N #V (G ), with probability p p(N):P(P(G )) 0whenp(N) 0τ (N)P(P(G )) 1whenp(N) τ (N)with P(P(G )) probability that the property is satisfied show that τ (N) P connectednesslog NNis a threshold function for the propertyMatilde Marcolli and Doris TsaoBrain Networks
for P connectedness show that for p(N) λ logNN :P(P(G )) 1for λ 1P(P(G )) 0for λ 1 to prove graph disconnected for λ 1 show growing number ofsingle node components in an Erdös–Rényi graph probability of a given node being aconnected component is (1 p)N 1 ; so typical number of singlenode components is N · (1 p)N 1 for large N this (1 p)N 1 e pN if p p(N) λ logNN this givese p(N) N e λ log N N λ for λ 1 typical number of single node componentsN · (1 p)N 1 N · N λ Matilde Marcolli and Doris TsaoBrain Networks
for λ 1 typical number of single vertex components goes tozero, but not enough to know graph becomes connected (largersize components may remain) probability of a set Sk of k vertices having no connection to therest of the graph (but possible connections between them) is(1 p)k(N k) typical number of sets of k nodes not connected to the rest ofthe graph N(1 p)k(N k)k Stirling’s formula k! k k e k gives for large N and k NN(1 p)k(N k) ( )k e k e kλ log N N k N λk e k(1 log k) 0kkfor p p(N) λ logNN with λ 1Matilde Marcolli and Doris TsaoBrain Networks
Phase transitions:at p logNN : graph becomes connectedat p N1 : emergence of one giant component use similar method: threshold function τ (N) N1 andprobabilities p(N) Nλ with either λ 1 or λ 1Case λ 1: starting at a vertex approximate counting of connected verticesin an Erdös–Rényi graph with a branching process B(N, Nλ ) replaces graph by a tree (overcounting of vertices) with typicalnumber of descendants N Nλ so in k steps from starting vertexexpected number of connections λk so typical size of the component connected to first vertex isbounded above by size obtained from branching processX1λk 1 λksmall sized componentsMatilde Marcolli and Doris TsaoBrain Networks
Branching process approximation to an Erdös–Rényi graph process(from Daron Acemoglu and Asu Ozdaglar, Lecture Notes on Networks)Matilde Marcolli and Doris TsaoBrain Networks
Case λ 1: process B(N, Nλ ) asymptotically Poisson with probability (ksteps)λke λk! probability ρ that tree obtained via this process is finite:recursive structure (overall tree finite if each tree starting fromnext vertices finite)Xλkρ e λ ρkk!kfixed point equation ρ e λ(ρ 1) one solution ρ 1 but another solution inside interval 0 ρ 1Matilde Marcolli and Doris TsaoBrain Networks
however. the branching process B(n, p) produces trees, but onthe graph G fewer vertices. after δN vertices have been added to a component via thebranching process starting from one vertex, to continue the processone has B(N(1 δ), p) correspondingly changing λ 7 λ(1 δ) (tocontinue to approximate same p of Erdös–Rényi process) progressively decreases λ(1 δ) as δ increases so branchingprocess becomes more likely to stop quickly typical size of the big component becomes (1 ρ)N whereρ ρ(λ) as above probability of finite tree, solution of ρ e λ(ρ 1)Matilde Marcolli and Doris TsaoBrain Networks
Robustness to lesions Remove a vertex v V (G ) with its star of edgesS(v ) {e E (G ) : v (e)}Gv G r S(v )measure change: e.g. change in size of largest component when keep removing more S(v )’s at various vertices, reach athreshold at which graph becomes fragmented in opposite way, keep adding edges with a certain probability,critical threshold where giant component arises, as discussedpreviouslyMatilde Marcolli and Doris TsaoBrain Networks
Core/Periphery core: subset of vertices highly connected to each other (hubs) periphery: nodes connected to core vertices but not with eachother maximal cliques: maximally connected subsets of nodesk-core decomposition: remove all S(v ) with deg(v ) k, remaininggraph G (k) k-core core index of v V (G ): largest k such that v V (G (k) )s-core G (s) : remove all S(v ) of vertices with weight w (v ) sMatilde Marcolli and Doris TsaoBrain Networks
k-core decomposition, from P.Hagmann, L.Cammoun, X.Gigandet,R.Meuli, C.J.Honey, V.J.Wedeen, O.Sporns, “Mapping the StructuralCore of Human Cerebral Cortex”, PLOS bio 2008Matilde Marcolli and Doris TsaoBrain Networks
Topology and flow of information along directed graphs networks with characteristic path length (close to min in arandom graph) path length min number of oriented edges or minimum totalweight of these edgeswalks, trails, pathswalk: sequence of oriented edges (target of one source ofnext): revisiting vertices and edges allowedtrail: same but no edge repetitions (edges visited only once)path: no edge and no vertex repetitions (both vertices andedges visited only once)Warning: terminology varies in the literatureMatilde Marcolli and Doris TsaoBrain Networks
two paths from U to V and a trail from U to V shortest path geodesics (with edge weights as metric) average of path length over all shortest path in the graphat vertex vi average i of lengths ij (vi , vj ) of shortestpaths starting at vi (and ending at any other vertex vj )average over verticesL X1 X1 i ijNN(N 1)iMatilde Marcolli and Doris Tsaoi6 jBrain Networks
main idea: brain networks with the shortest average path lengthintegrate information better in case of a graph with several connected components, for vi andvj not in the same component usually take ij , then better touse harmonic mean 1X N(N 1) 1iji6 jor its inverse, the global efficiency:X1 1ijN(N 1)i6 jMatilde Marcolli and Doris TsaoBrain Networks
The Graph Laplacianmeasuring flow of information in a graph δ (δij ) diagonal matrix of valencies δii deg(vi ) adjacency matrix A (weighted with wij ) Laplacian G δ Aˆ G I Aδ 1 or symmetrized form normalized Laplacian ˆ s I δ 1/2 Aδ 1/2 G wij /δii probability of reaching vertex vj after vi along arandom walk searchˆ G counts connected components dimension of Ker eigenvalues and eigenvectors give decomposition of the graphinto “modules”Matilde Marcolli and Doris TsaoBrain Networks
Dynamics in brain networks fast dynamics 100 millisecond timescale:variability in functional coupling of neurons and brain regions,underlying functional anatomy unchanged; also slow dynamics:long lasting changes in neuron interaction due to plasticity.growth, rewiring types of dynamics: diffusion processes, random walks,synchronization, information flow, energy flow topology of the graph plays a role in the spontaneous emergenceof global (collective) dynamical states multiscale dynamics: dynamics at a scale influenced by statesand dynamics on larger and smaller scales mean field model: dynamics at a scale averaging over effects atall smaller scalesMatilde Marcolli and Doris TsaoBrain Networks
synchronization of a system of coupled oscillators at vertices withcoupling along edges if graph very regular (eg lattice) difficult to achieve synchronizedstates small-world networks are easier to synchronize fully random graphs synchronize more easily but synchronizedstate also very easily disrupted: difficult to maintainsynchronization more complex types of behavior when non-identical oscillators(different weights at different vertices) and additional presence ofnoise still open question: what is the role of topology and topologychanges in the graph in supporting self-organized-criticalityMatilde Marcolli and Doris TsaoBrain Networks
Fundamentals of Brain Network Analysis, Elsevier, 2016 Olaf Sporns, Networks of the Brain, MIT Press, 2010 Olaf Sporns, Discovering the Human Connectome, MIT Press, 2012 Fan Chung, Linyuan Lu, Complex Graphs and Networks, American Mathematical Society, 2004 L aszl o Lov asz, Large Networks and Graph Limits, American Mathematical Society, 2012
Sheep Brain Dissection Guide 4. Find the medulla (oblongata) which is an elongation below the pons. Among the cranial nerves, you should find the very large root of the trigeminal nerve. Pons Medulla Trigeminal Root 5. From the view below, find the IV ventricle and the cerebellum. Cerebellum IV VentricleFile Size: 751KBPage Count: 13Explore furtherSheep Brain Dissection with Labeled Imageswww.biologycorner.comsheep brain dissection questions Flashcards Quizletquizlet.comLab 27- Dissection of the Sheep Brain Flashcards Quizletquizlet.comSheep Brain Dissection Lab Sheet.docx - Sheep Brain .www.coursehero.comLab: sheep brain dissection Questions and Study Guide .quizlet.comRecommended to you b
I Can Read Your Mind 16 How the Brain Creates the World 16 Part I Seeing through the Brain's Illusions 19 1 Clues from a Damaged Brain 21 Sensing the Physical World 21 The Mind and the Brain 22 When the Brain Doesn't Know 24 When the Brain Knows, But Doesn't Tell 27 When the Brain Tells Lies 29 How Brain Activity Creates False Knowledge 31
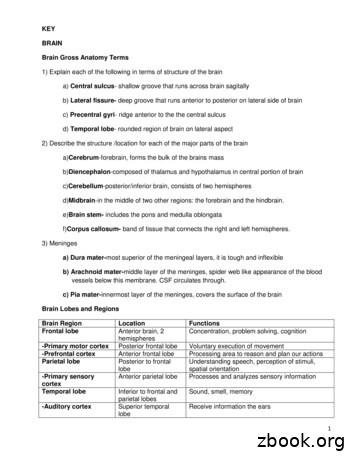
1 KEY BRAIN Brain Gross Anatomy Terms 1) Explain each of the following in terms of structure of the brain a) Central sulcus- shallow groove that runs across brain sagitally b) Lateral fissure-deep groove that runs anterior to posterior on lateral side of brain c) Precentral gyri- ridge anterior to the the central sulcus d) Temporal lobe- rounded region of brain on lateral aspect
1 Introduction to Combinatorial Algebraic Topology Basic Topology Graphs to Simplicial Complexes Posets to Simplicial Complexes 2 Permutation Patterns Introduction and Motivation Applying Combinatorial Algebraic Topology Kozlov, Dimitry. Combinatorial algebraic topology. Vol. 21. Springer Science & Business Media, 2008.
TOPOLOGY: NOTES AND PROBLEMS Abstract. These are the notes prepared for the course MTH 304 to be o ered to undergraduate students at IIT Kanpur. Contents 1. Topology of Metric Spaces 1 2. Topological Spaces 3 3. Basis for a Topology 4 4. Topology Generated by a Basis 4 4.1. In nitude of Prime Numbers 6 5. Product Topo
a topology on R, the standard topology on R. Thus the open sets are unions of open intervals. A closed interval [c,d] is then closed in this topology. A half-open interval ]a,b],a bis neither open nor closed for this topology. We shall verify later that and R are the only subsets of R which are both open and closed (see (1.9.1)).
A hybrid neural network architecture, namely U-SE-ResNet, as the generator for TopologyGAN. 2 Related Work Our review focuses on studies that highlight topology optimization, deep learning for topology optimization, gener-ative adversarial networks (GAN), and two network architec-tures closely related to our work. 2.1 Topology Optimization and SIMP
Archaeological illustration. Cambridge Manuals in Archaeology. Cambridge University Press, 1989. A clearly presented manual describing the various purposes, approaches, conventions, and techniques for archaeological drawings. The number of different types of drawings explained is impressive and necessary for anyone attempting to understand such drawings, especially if attempting to use such .