GraphBit: Bitwise Interaction Mining Via Deep Reinforcement Learning
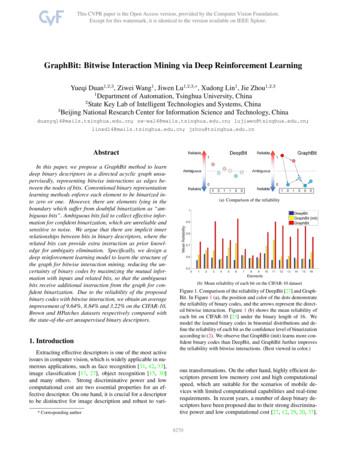
GraphBit: Bitwise Interaction Mining via Deep Reinforcement LearningYueqi Duan1,2,3 , Ziwei Wang1 , Jiwen Lu1,2,3, , Xudong Lin1 , Jie Zhou1,2,31Department of Automation, Tsinghua University, China2State Key Lab of Intelligent Technologies and Systems, China3Beijing National Research Center for Information Science and Technology, Chinaduanyq14@mails.tsinghua.edu.cn; zw-wa14@mails.tsinghua.edu.cn; .cn; jzhou@tsinghua.edu.cnAbstractIn this paper, we propose a GraphBit method to learndeep binary descriptors in a directed acyclic graph unsupervisedly, representing bitwise interactions as edges between the nodes of bits. Conventional binary representationlearning methods enforce each element to be binarized into zero or one. However, there are elements lying in theboundary which suffer from doubtful binarization as “ambiguous bits”. Ambiguous bits fail to collect effective information for confident binarization, which are unreliable andsensitive to noise. We argue that there are implicit innerrelationships between bits in binary descriptors, where therelated bits can provide extra instruction as prior knowledge for ambiguity elimination. Specifically, we design adeep reinforcement learning model to learn the structure ofthe graph for bitwise interaction mining, reducing the uncertainty of binary codes by maximizing the mutual information with inputs and related bits, so that the ambiguousbits receive additional instruction from the graph for confident binarization. Due to the reliability of the proposedbinary codes with bitwise interaction, we obtain an averageimprovement of 9.64%, 8.84% and 3.22% on the CIFAR-10,Brown and HPatches datasets respectively compared withthe state-of-the-art unsupervised binary descriptors.1. IntroductionExtracting effective descriptors is one of the most activeissues in computer vision, which is widely applicable in numerous applications, such as face recognition [31, 42, 33],image classification [17, 27], object recognition [15, 30]and many others. Strong discriminative power and lowcomputational cost are two essential properties for an effective descriptor. On one hand, it is crucial for a descriptorto be distinctive for image description and robust to vari* Corresponding author(a) Comparison of the reliability(b) Mean reliability of each bit on the CIFAR-10 datasetFigure 1. Comparison of the reliability of DeepBit [27] and GraphBit. In Figure 1 (a), the position and color of the dots demonstratethe reliability of binary codes, and the arrows represent the directed bitwise interaction. Figure 1 (b) shows the mean reliability ofeach bit on CIFAR-10 [23] under the binary length of 16. Wemodel the learned binary codes in binomial distributions and define the reliability of each bit as the confidence level of binarizationaccording to (2). We observe that GraphBit (init) learns more confident binary codes than DeepBit, and GraphBit further improvesthe reliability with bitwise interactions. (Best viewed in color.)ous transformations. On the other hand, highly efficient descriptors present low memory cost and high computationalspeed, which are suitable for the scenarios of mobile devices with limited computational capabilities and real-timerequirements. In recent years, a number of deep binary descriptors have been proposed due to their strong discriminative power and low computational cost [27, 12, 29, 20, 37].18270
Binary descriptors substitute real-valued elements with binary codes which are efficient for storage and matching,while deep learning obtains high quality representation bytraining numerous parameters with large amount of data.For most existing deep binary descriptor learning approaches, binarization is an essential step to quantize eachreal-valued element into zero or one, which enhances theefficiency of the descriptors at the cost of quantizationloss [12]. However, to the best of our knowledge, thesemethods directly perform binarization on the real-valued elements to obtain binary codes, which fail to consider theirreliability. If a real-valued element lies in the boundary ofthe binarization for an input image, it would suffer from anunreliable result and an “ambiguous bit” is obtained. Forexample, the result of a sign function based binarization isdoubtful for a real-valued element close to zero. Ambiguous bits fail to receive effective instruction from the corresponding inputs for confident binarization, which presentlittle discriminative power and are sensitive to noise.We argue that there are implicit relationships betweenbits for the learned binary codes, and the related bits canprovide extra instruction to the ambiguous bits as priorknowledge. For example, it is ambiguous to decide whethera person is tall or short in 5 feet 9 inches. However, theanswer becomes more certain if we consider an additionalgender bit of female or an age bit of young child. In thispaper, we propose a GraphBit method to eliminate the ambiguity through bitwise interaction mining, where we represent binary codes in a directed acyclic graph. The nodes ofthe graph are the elements in binary descriptors and the directed edges represent bitwise connections. As the learneddeep binary descriptors usually fail to present clear physicalmeanings where the relationships between bits are implicit,we design a deep reinforcement learning model to decidethe structure of the graph for bitwise interaction mining.More specifically, we perform a sigmoid function at theend of CNN for normalization, modelling the normalizedelements as the possibilities of being quantized into one ina binomial distribution. The probabilistic model describesthe reliability of binarization, and we formulate the relationships between bits as conditional probabilities. We simultaneously train the parameters of CNN and the structure ofthe graph in an unsupervised manner, maximizing the mutual information of each bit with the observed inputs andthe related bits for ambiguity elimination. For the deep reinforcement learning based bitwise interaction mining, wedefine the action to add or remove a directed connection between two nodes, and the state is the current structure ofthe graph. In Figure 1, DeepBit ignores the reliability during the training procedure, GraphBit (init) only maximizesthe mutual information without bitwise interaction mining,and GraphBit mines the relationships between bits throughdeep reinforcement learning. We observe that both mutualinformation maximization and bitwise interaction enhancethe reliability of the binary codes. Extensive experimentalresults show that GraphBit outperforms most existing unsupervised binary descriptors due to its strong reliability.2. Related WorkBinary Descriptors: Binary descriptors have attractedmuch attention in computer vision due to their efficiency for storage and matching, where early works can betraced back to binary robust independent elementary feature (BRIEF) [8], binary robust invariant scalable keypoint(BRISK) [25], oriented FAST and rotated BRIEF (ORB) [35] and fast retina keypoint (FREAK) [1]. BRIEF computed binary descriptors through the intensity different testsbetween pixels. BRISK obtained scale and rotation invariance by leveraging a circular sampling pattern. ORB improved BRIEF by applying scale pyramids and orientationoperators. FREAK utilized retinal sampling grid for acceleration.As hand-crafted binary descriptors are heuristics andusually require strong prior knowledge, a number of learning based approaches have been proposed and achievedoutstanding performance [41, 46, 44, 14]. For example,Strecha et al. [41] proposed LDA-Hash by applying lineardiscriminant analysis (LDA) before binarization. Trzcinski et al. [46] presented D-BRIEF by learning discriminative projections through similarity relationships. Theyalso learned hash functions with boosting to obtain BinBoost [44]. Fan et al. [14] proposed a receptive fields descriptor (RFD) by thresholding responses of two different receptive fields, rectangular pooling area and Gaussianpooling area.More recently, several deep binary descriptor learningapproaches have been proposed [13, 27, 12, 29, 20, 37],which achieve the state-of-the-art performance. For example, Lin et al. [27] proposed DeepBit by training a deepneural network with essential properties in an unsupervisedmanner. Duan et al. [12] presented a deep binary descriptor with multi-quantization (DBD-MQ) to minimize thequantization loss of binarization with a K-autoencoders network. Shen et al. [37] proposed textual-visual deep binaries(TVDB) to simultaneously encode the detailed semantics ofimages and sentences. However, these deep binary descriptors fail to exploit bitwise interactions, which suffer fromunreliable ambiguous bits.Deep Reinforcement Learning: Reinforcement learning aims to learn the policy of sequential actions fordecision-making problems [43, 21, 28]. Due to the recent success in deep learning [24], deep reinforcement learning has aroused more and more attention by combining reinforcement learning with deep neural networks [32, 38].Deep reinforcement learning algorithms have obtained verypromising results [39, 32, 38], which can be mainly divided8271
Figure 2. The flowchart of the proposed GraphBit. For each input image, we first learn a normalized feature with a pre-trained CNN byreplacing the softmax layer with a fully connection layer followed by a sigmoid function. The normalized feature ranges from 0 to 1,representing the possibility of being binarized into one for clear description of reliability. Then, we simultaneously train the parametersof CNN and the structure of the graph for ambiguity elimination, mining bitwise relationships through deep reinforcement learning. Weoptimize the parameters with back-propagation in an unsupervised manner.into two categories: deep Q-networks and policy gradient.For example, Mnih et al. [32] played ATARI games throughdeep Q-networks. Silver et al. [38] designed a programnamed AlphaGo with Monte-Carlo tree search based deepreinforcement learning, which defeated the world championin the game of Go.More recently, deep reinforcement learning approacheshave been employed in many computer vision applications [7, 50, 9, 22, 26, 34]. For example, Kong et al. [22] proposed a collaborative multi-agent deep reinforcement learning algorithm to exploit the contextual information for jointobject search. Liang et al. [26] presented a deep variationstructured reinforcement learning (VRL) approach to graspglobal visual cues. However, to our best knowledge, no relevant deep reinforcement learning works have been focusedon the fundamental problem of binary representation extraction, which is of significant importance in a variety of visualanalysis tasks.3. Proposed ApproachIn this section, we first introduce the reliability of binarycodes, and then present the objective function of GraphBit.Lastly, we detail the deep reinforcement learning model forbitwise interaction mining.3.1. Reliability of Binary CodesThe reliability of binary codes is an essential property inbinary descriptor learning, which determines the credibilityof each bit. As aforementioned, ambiguous bits may leadto weak discriminative power and unrobustness, as they failto collect effective information from the inputs. However, most existing approaches directly perform binarizationon real-valued elements without considering the reliability,which suffer from ambiguous bits.In this paper, we aim to learn reliable binary codes andwe first define the confidence of binarization. As shown inFigure 2, we initialize the CNN with the pre-trained 16 layers VGG network [40], substituting the softmax layer witha fully connection layer followed by an activation functionof sigmoid. Unlike most existing binary descriptors whichdirectly utilize a sign function for binarization, we first perform a sigmoid function at the end of CNN to normalizeeach element in the range of 0 to 1 for better reliability estimation. The normalized elements are regarded as the possibilities of being quantized to one in a binomial distribution,and the strategy of binarization is shown as follows:(1 0.5 6 f (tkn ) 6 1bkn (1)0 0 6 f (tkn ) 0.5,where tkn represents the kth real-valued element of the nthinput image without considering bitwise interaction, f (tkn )is the normalized value and bkn is the corresponding bit.As it is unlikely to promise each element to be zero orone, we choose the binarization results with higher possibilities. Obviously, the binarization results are more convincing for the f (tkn ) close to 0 or 1, while it is ambiguous for the values near 0.5. Let bk p(bk ) be the variable of the kth bit, following a binomial distribution ofp(bk 1 xn ) f (tkn ). With the binarization strategyof (1), we obtain the reliability of binary codes as follows:p(bk bkn xn ) f (tkn ) 0.5 0.5,(2)which ranges from 0.5 to 1. Our goal is to maximize theconfidence level of binarization for reliable binary codesthrough bitwise interaction mining. In the following, wedenote p(bk bkn xn ) as p(bkn xn ) for short.8272
3.2. Objective Function2) J2 encourages the independent bits brn to obtain mostinformation from the input samples by maximizing themutual information, which reduces the uncertainty inbrn with xn observed according to (3). For the interacted bits bsn , they simultaneously receive instructionfrom the corresponding inputs xn and the related bitsbtn . This term ensures the reliability of the learned binary codes, where each bit chooses to be instructed byeither only inputs or with additional related bits.Let X [x1 , x2 , · · · , xN ] be the N input samples ofthe image set. The objective of GraphBit is to simultaneously learn deep binary descriptors B [b1 , b2 , · · · , bN ]and the structure of graph Φ {(bTt , bTs )} which represents the directed connections from the tth bit to the sthbit. In order to describe bitwise relationships, we denotethe interaction between random variables X and Y by mutual information I(X; Y ), which describes the decrease ofentropy of X when Y is tractable:I(X; Y ) H(X) H(X Y ),3) J3 aims to prevent the interacted bits to become trivial. Under the guidance of J2 , those ambiguous bitsthat fail to collect effective information from the inputs may tend to receive extra directions from othermore reliable bits. However, they may become redundant as a repeat of the related bits if suffering from toostrong instructions. The goal of J3 is to guarantee theindependence of the interacted bits.(3)where the entropyH(X) Ex p(X) [log p(x)]H(X Y ) Ey p(Y ) [Ex p(X Y ) [log p(x y)]]. (5)(4)Here, H(X) and H(X Y ) reveal the uncertainty of thevariables. Large I(X; Y ) represents much reduction of uncertainty in X when Y is observed, and in the extreme casewhen X and Y are independent, I(X; Y ) is equal to zero.Inspired by the above motivations, we formulate the following objective function to learn GraphBit:min J αNXn 1(XI(brn ; xn ) n 1 brn b/ Ts I(brn ; xn )J1 αJ2 βJ3NKXX(bkn 0.5) 2 k 1 We apply variational information maximization to simplify J2 in (6) with the upper bounding, which is then approximated with Monte Carlo simulation [5, 10].The first part of J2 can be rewritten as follows:βN XXXI(bsn ; xn , btn )) H(brn ) H(brn xn ) H(brn ) Exn X [Eb′rn p(brn xn )[log p(b′rn xn )]] H(brn ) Exn X [DKL (p(· xn ) q(· xn )) Eb′rn p(brn xn ) [log q(b′rn xn )]]H(brn ) Exn X [Eb′rn p(brn xn )[log q(b′rn xn )]],Φ p(bsn xn ) p(bsn xn , btn ) 2 , (6)n 1 Φwhere K is the length of the binary descriptors and(bTt , bTs ) Φ. α and β are two parameters to balance theweights of different terms. bsn represents the binarizationresult under the instruction of btn , and we use an additionalbitwise weight of wts to represent bsn based on the normalization result of a weighted sum:p(bsn xn ) f (tsn ) 0.5 0.5,Xp(bsn xn , btn ) f (tsn wts ttn ) 0.5 0.5.(7)(8)tWe detail the physical meanings of the three terms in theobjective function as follows:1) J1 is to make each bit in the learned GraphBit evenlydistributed. If an element in the learned binary descriptors stay the same for all the samples, it would presentno discriminative power. Instead, we encourage eachbit equal to zeros for half of the samples and ones forthe others to convey more information.(9)where q(·) is the auxiliary distribution for the posterior distribution p(·). In this paper, we parametrize q(b′rn xn )based on the reliability of binary codes defined in (2). Whenthe distribution of q(·) approaches the distribution of p(·),the bound is tight because DKL (q(·) p(·)) 0. In ourexperiments, we specially set q(b′rn xn ) trn 0.5 toobtain large magnitude by the log function for strict constraint of reliability. For simplicity, H(brn ) is regarded tobe constants because each bit should have a prior equal possibility to be zero or one.Similarly, the second part in J2 can be rewritten as follows:I(bsn ; xn , btn ) H(bsn ) Exn X [Eb′sn p(bsn xn ,btn )[log q(b′sn xn , btn )]].(10)We apply the stochastic gradient decent with backpropagation to train the CNN model in an unsupervised manner.3.3. Deep Reinforcement Learning for Bitwise Interaction MiningMining bitwise interaction for ambiguity elimination canbe viewed as a Markov Decision Process (MDP), which is8273
of actions, which can be represented as a transition matrixtWt RK K . The element wij [0, 1] represents the probability of the connection from the ith bit to the jth bit. Weselect the actions based on the following rules:t1) Add: We connect the ith bit to the jth bit if wij tmax{Wt } together with wij k1 .2) Remove: We disconnect the original edge between thet6 k2 .ith bit and the jth bit if wij3) Stop: We terminate the current epoch of bitwise interaction mining for convergence or achieving the maximum time step.In this paper, we gradually increase the parameters k1and k2 during the iterations, where the maximum values fork1 and k2 are 0.8 and 0.2, respectively.Reward Function: We define the reward functionR(S, A) in round t as following:Figure 3. An explanation of deep reinforcement learning based bitwise interaction mining. In this example, we sequentially add directed connections of the 4th-5th bits, the 1st-3rd bits, the 6th-5thbits and the 6th-3rd bits, and then remove the connection of the4th-5th bits. We repeat the process of bitwise interaction mininguntil finalizing the structure of graph.formally defined as M {S, A, T (S, A), R(S, A)}.At each step, the agent takes the action to add or removea directional connection between bits based on the currentstructure of the graph, which iteratively explores the bitwiseinteraction to maximize the reward. The policy network recurrently adds and removes the edges until convergence orachieving the maximum step. At the end of the sequence,we retrain the parameters of CNN with the learned structureof graph under the guidance of the objective function.States: The state space S represents the current structure of the graph, which can be defined as a binary matrixsWs {0, 1}K K . For the element wij Ws , it equals to one if there is a directed edge between the ith bit andthe jth bit, and equals to zero otherwise. GraphBit undera zero matrix for Ws is equivalent to existing deep binarydescriptors without bitwise interactions as a special case.Action: Given the current graph Ws , the agent aims toselect one action from all possible connections and disconnections. AS set of actions divided into three cateS is thegories: Ac Ar {stop}. The action to add a bitwise edgeis denoted as Ac , while Ar represents to remove bitwiseconnections. The action of stop is executed for convergenceor the maximum time step. Figure 3 shows an example oftransition of stages with the actions.′Transition Function: T (S, A) S is the transitionfunction which shows the movement of the stage. T is constructed under the observation of states and performancer(st , at ) J(st ) J(st 1 )(11)where r(st , at ) R(S, A) is the returning reward for theaction at in the state st , and J(st ) is the loss of the objectivefunction in the state st . We consider the bitwise interactionin high quality if it leads to lower loss in the unsupervisedlearning, which simultaneously enhances the discriminativepower and the reliability of the learned GraphBit.We employ a CNN network with the deconvolution layerin the end as our policy network. More specifically, the policy network has three convolutional layers, followed by twofully connected layers and two deconvolutional layers. Weapply ReLU as the activation function in the middle layersand sigmoid for the last layer. We also perform dropout toprevent from overfitting. The input of the policy network isthe state matrix Ws , and the output of the network predictsthe probability of actions with Wt .We utilize the REINFORCE algorithm [49] to update parameters in the policy network in response to the rewardsfrom the environment. The objective is to maximize the expected reward over the entire GraphBit learning process:max Z(θ) Eπ [θTXγrt (st , at )],(12)t 1where θ represents the parameters of the policy network, πis the selected policy and γ is the discount factor. We set γas 0.9 throughout the experiments.Following the REINFORCE algorithm, we obtain thegradient of (12) as follows:X θ Z θ [π(at st )rt ]qt ,at Xrt π(at st ) θ log π(at st )qt ,at 8274Eπ [rt θ log π(at st )].(13)
Precision Rate0.450.40.50.45Precision 100.20.4Recall Rate(a) 16 t0.55Precision Rate0.60.550.60.8100.2Recall Rate0.40.60.81Recall Rate(b) 32 bits(c) 64 bitsFigure 4. Comparison of Precision/Recall curves on the CIFAR-10 dataset under varying binary lengths (a) 16 bits, (b) 32 bits and (c) 64bits with the state-of-the-art unsupervised binary descriptors.We apply the sampled sequences (s1 , a1 ; .; sTk , aTk )for the approximation of (13), and obtain the gradient ofpolicies by sampling for M times:TkMX1 X θ log π(at st ),Rk θ Z Mt 0Table 1. Comparison of mean average precision (mAP) (%) of top1,000 returned images with the state-of-the-art unsupervised binary descriptors on CIFAR-10.MethodKMH [18]SphH [19]SpeH [48]SH [36]PCAH [47]LSH [2]PCA-ITQ [16]DH [13]DeepBit [27]DBD-MQ [12]GraphBit (init)GraphBit(14)k 1where Tk is the number of steps in the sampled sequencesand Rk represents the reward achieved in the kth sequence.4. ExperimentsIn this section, we evaluated our GraphBit on threedatasets for patch retrieval, image matching and patch verification tasks to demonstrate the effectiveness of the proposed GraphBit, where the CIFAR-10 [23], Brown [6] andHPatches [4] datasets were employed, respectively. BesidesGraphBit, we also tested the performance of our approachwithout bitwise interaction mining by training with only J1and the first part of J2 as GraphBit (init).Following [27],we resized each input image into 256 256 at first, andthen cropped it to 224 224 for background removal. Weempirically set the parameters α and β as 0.2 and 0.4 tobalance the weights, respectively.4.1. Results on CIFAR-10The CIFAR-10 dataset [23] consists of 10 categories andeach class contains 6,000 images. We applied 50,000 images as the training set and the other 10,000 as the test set.We followed the standard evaluation protocol [23] to evaluate the mean average precision (mAP) under different binary length of 16 bits, 32 bits and 64 bits.Comparisons with the State-of-the-Art UnsupervisedBinary Descriptors: We compared our GraphBit withseveral unsupervised binary descriptors on the CIFAR-10dataset. Among the listed approaches, deep hashing (DH),DeepBit and DBD-MQ are the state-of-the-art unsuperviseddeep binary descriptors. Table 1 illustrates the comparisonwith mean average precision (mAP) and Figure 4 shows16 1.5327.9532.1532 6.5032.7736.7464 1.8536.1639.90Table 2. Comparison of mean average precision (mAP) (%) of top1,000 returned images under different learning strategies of GraphBit on CIFAR-10.MethodGraphBit (J1 )GraphBit (J1 J2 )GraphBit (J1 J2 J3 )Independent Bits21.4527.95-Interacted Bits26.2030.4332.15the Precision/Recall curves. DBD-MQ achieves the stateof-the-art performance, while GraphBit improves the mAPby 10.62%( 32.15%-21.53%), 10.24%( 36.74%-26.50%),8.05%( 39.90%-31.85%) in the settings of 16-bit, 32-bitand 64-bit, respectively.We observe that GraphBit obtains a 9.64% improvementon average on CIFAR-10 compared with the unsupervisedbinary descriptors, while GraphBit (init) also improves themAP by 5.67% even without bitwise interaction mining.With the comparison of the reliabilities shown in Figure 1at the beginning of the paper, we see that more reliable binary codes achieve better results. For GraphBit (init), theadvantages mainly come from the second term J2 of theobjective function, which reduces the uncertainty of bina8275
Table 3. Comparison of 95% error rates (ERR) on the Brown dataset with the state-of-the-art binary descriptors. Unsupervised binarydescriptor include BRISK, BRIEF, DeepBit and DBD-MQ, and supervised binary descriptors include LDAHash, D-BRIEF, BinBoost andRFD. The real-valued feature SIFT is provided for reference.YosemiteNotre 9.6653.3921.6719.4028.3324.72Notre 919.3525.0021.18LibertyNotre 8.3215.25110.90.90.80.80.80.70.70.6Boosted 50.40.30.10.6Boosted 50.40.30.20.10True Positive 738.5951.4047.5419.2415.8632.8329.750.70.6Boosted 50.40.30.1000.20.40.60.8100.20.40.60.8False Positive RateFalse Positive RateFalse Positive Rate(a) Yosemite-Notre Dame(b) Yosemite-Liberty(c) Notre Dame-Yosemite10.90.80.80.80.70.70.6Boosted 50.40.30.20.10.6Boosted 50.40.30.20.10True Positive Rate10.9True Positive Rate10.90.20.40.60.8110.70.6Boosted 57.1552.9547.2922.8816.9952.5849.640.200True Positive RateNotre 9614.5051.6249.940.9True Positive RateTrue Positive RateTrainTestSIFT [30] (128 bytes)BRISK [25] (64 bytes)BRIEF [8] (32 bytes)DeepBit [27] (32 bytes)DBD-MQ [12] (32 bytes)LDAHash [41] (16 bytes)D-BRIEF [46] (4 bytes)BinBoost [44] (8 bytes)RFD [14] (50-70 bytes)GraphBit (init) (32 bytes)GraphBit (32 bytes)000.20.40.60.8100.20.40.6False Positive RateFalse Positive RateFalse Positive Rate(d) Notre Dame-Liberty(e) Liberty-Notre Dame(f) Liberty-Yosemite0.81Figure 5. Comparison of ROC curves on the Brown dataset with several binary descriptors.ry codes by mutual information maximization. As reliablebits receive more effective information from the inputs forconfident quantization, they present stronger discriminativepower and robustness. For GraphBit, each bit is also allowed to be instructed by other related bits to further enhance the reliability and obtains better performance. Thenumbers of bitwise connections are 22, 198 and 880 for 16bits, 32 bits and 64 bits, respectively.Influences of Different Learning Strategies: In orderto investigate the contributions of bitwise interactions anddifferent terms in GraphBit, we evaluated the performanceon CIFAR-10 under different training strategies with bina-ry length of 16. We preserved J1 in all the settings to ensure the variation of each bit. As aforementioned, GraphBit(init) is the situation of training independent bits with J1and J2 . Table 2 shows that bitwise interaction mining improves the experimental results with different training termsby exploring implicit relationships between bits. Experimental results also demonstrate the effectiveness of J2 andJ3 . While J2 aims to enhance the reliability of binary codesthrough mutual information maximizing, J3 prevents fromtrivial bits with over-strong bitwise instructions. Both J2and J3 improve the experimental results, and the best performance can be achieved when all the terms are used to-8276
gether with bitwise interactions.Computational Time: Our hardware equips with a 2.8GHz CPU and a 32G RAM, and we utilized a GTX 1080Ti GPU for acceleration. We evaluated the total time ofextracting one probe feature and retrieving from 50,000gallery features, where a 32-bit GraphBit took 0.016s toobtain retrieval result. HOG [11] and SIFT [30] required0.030s and 0.054s, respectively. GraphBit substitutes theHamming distance for the Euclidean distance and presentshigher matching speed. As for the storage cost, a 32-bitGraphBit only required 4 bytes for each image, while 9bytes were needed for HOG and 128 bytes for SIFT.Table 4. Comparison of mean average precision (mAP) (%) withunsupervised binary codes and other baseline methods under various tasks on HPatches.4.2. Results on Brownand patch retrieval. HPatches consists of 116 sequences intotal, splitting into 57 with photometric changes and 59 withsignificant geometric deformations.We followed the standard evaluation protocol [4] to report the performance of mean average precision (mAP) onthe three visual analysis tasks. We compared GraphBit withunsupervised binary descriptors including BRIEF [8], ORB [
Deep Reinforcement Learning: Reinforcement learn-ing aims to learn the policy of sequential actions for decision-making problems [43, 21, 28]. Due to the recen-t success in deep learning [24], deep reinforcement learn-ing has aroused more and more attention by combining re-inforcement learning with deep neural networks [32, 38].
Feb 22, 2021 · Brand Standards Use this guide as a high-level overview of how Bitwise syncs into one cohesive brand. Last updated: 2/22/2021. BITWISE INDUSTRIES 1 Voice Boilerplate In marketing, a boilerplate is a short paragraph summarising a company and is used across
Operation C Java MIPS Shift left sll Shift right srl Bitwise AND & & and, andi Bitwise OR or, ori Bitwise NOT nor ! Useful for extracting and inserting groups of bits in a word s . The University of Adelaide, School of Computer Science 17 January 2011 Chapter 2
Figure 2: Overview: (a) Computing-centric ap-proach, moving tons of data to CPU and write back. (b) The proposed Pinatubo architecture, performs n-row bitwise operations inside NVM in one step. We propose Pinatubo to accelerate the bitwise operations inside the NVM-based main memory. Fig. 2 shows the overview of our design.
DATA MINING What is data mining? [Fayyad 1996]: "Data mining is the application of specific algorithms for extracting patterns from data". [Han&Kamber 2006]: "data mining refers to extracting or mining knowledge from large amounts of data". [Zaki and Meira 2014]: "Data mining comprises the core algorithms that enable one to gain fundamental in
enable mining to leave behind only clean water, rehabilitated landscapes, and healthy ecosystems. Its objective is to improve the mining sector's environmental performance, promote innovation in mining, and position Canada's mining sector as the global leader in green mining technologies and practices. Source: Green Mining Initiative (2013).
Preface to the First Edition xv 1 DATA-MINING CONCEPTS 1 1.1 Introduction 1 1.2 Data-Mining Roots 4 1.3 Data-Mining Process 6 1.4 Large Data Sets 9 1.5 Data Warehouses for Data Mining 14 1.6 Business Aspects of Data Mining: Why a Data-Mining Project Fails 17 1.7 Organization of This Book 21 1.8 Review Questions and Problems 23
Data Mining and its Techniques, Classification of Data Mining Objective of MRD, MRDM approaches, Applications of MRDM Keywords Data Mining, Multi-Relational Data mining, Inductive logic programming, Selection graph, Tuple ID propagation 1. INTRODUCTION The main objective of the data mining techniques is to extract .
FINAL YEAR MEng PROJECT Reprap Colour Mixing Project James Corbett 1st May 2012 . make the technology widely available for home users and projects such as RepRap have become much more widespread. RepRap is an open source project started by Adrian Bowyer of Bath University in 2005 which was designed around the ideal of creating a low cost home printer that could self replicate a larger .