CSC 411: Lecture 03: Linear Classi Cation - Department Of Computer .
CSC 411: Lecture 03: Linear ClassificationRichard Zemel, Raquel Urtasun and Sanja FidlerUniversity of TorontoZemel, Urtasun, Fidler (UofT)CSC 411: 03-Classification1 / 24
Examples of ProblemsWhat digit is this?How can I predict this? What are my input features?Zemel, Urtasun, Fidler (UofT)CSC 411: 03-Classification2 / 24
RegressionWhat do all these problems have in common?Categorical outputs, called labels(eg, yes/no, dog/cat/person/other)Assigning each input vector to one of a finite number of labels is calledclassificationBinary classification: two possible labels (eg, yes/no, 0/1, cat/dog)Multi-class classification: multiple possible labelsWe will first look at binary problems, and discuss multi-class problems laterin classZemel, Urtasun, Fidler (UofT)CSC 411: 03-Classification3 / 24
TodayLinear Classification (binary)Key Concepts:IIIIClassification as regressionDecision boundaryLoss functionsMetrics to evaluate classificationZemel, Urtasun, Fidler (UofT)CSC 411: 03-Classification4 / 24
Classification vs RegressionWe are interested in mapping the input x X to a label t YIn regression typically Y Now Y is categoricalZemel, Urtasun, Fidler (UofT)CSC 411: 03-Classification5 / 24
Classification as RegressionCan we do this task using what we have learned in previous lectures?Simple hack: Ignore that the output is categorical!Suppose we have a binary problem, t { 1, 1}Assuming the standard model used for (linear) regressiony (x) f (x, w) wT xHow can we obtain w?Use least squares, w (XT X) 1 XT t. How is X computed? and t?Which loss are we minimizing? Does it make sense? square (w, t) N1 X (n)(t wT x(n) )2N n 1How do I compute a label for a new example? Let’s see an exampleZemel, Urtasun, Fidler (UofT)CSC 411: 03-Classification6 / 24
Classification as RegressionA dimensional1D example:Oneexample (input x is 1-dim)xThe colors indicate labels (a blue plus denotes that t (i) is from the firstclass, red circle that t (i) is from the second class)Greg Shakhnarovich (TTIC)Zemel, Urtasun, Fidler (UofT)Lecture 5: Regularization, intro to classificationCSC 411: 03-ClassificationOctober 15, 201311 / 17 / 24
Decision RulesOur classifier has the formf (x, w) wo wT xA reasonable decision rule is(1y 1if f (x, w) 0otherwiseHow can I mathematically write this rule?y (x) sign(w0 wT x)What does this function look like?Zemel, Urtasun, Fidler (UofT)CSC 411: 03-Classification8 / 24
Decision RulesA 1D example:yŷ 1 1ŷ 1xw0 w T x-1How can I mathematically write this rule?Greg Shakhnarovich (TTIC)y (x) sign(w0 wT x)Lecture 5: Regularization, intro to classificationOctober 15, 201311 / 15This specifies a linear classifier: it has a linear boundary (hyperplane)w0 wT x 0which separates the space into two ”half-spaces”Zemel, Urtasun, Fidler (UofT)CSC 411: 03-Classification9 / 24
Example in 1DThe linear classifier has a linear boundary (hyperplane)w0 wT x 0which separates the space into two ”half-spaces”In 1D this is simply a thresholdZemel, Urtasun, Fidler (UofT)CSC 411: 03-Classification10 / 24
Example in 2DThe linear classifier has a linear boundary (hyperplane)w0 wT x 0which separates the space into two ”half-spaces”In 2D this is a lineZemel, Urtasun, Fidler (UofT)CSC 411: 03-Classification11 / 24
Example in 3DThe linear classifier has a linear boundary (hyperplane)w0 wT x 0which separates the space into two ”half-spaces”In 3D this is a planeWhat about higher-dimensional spaces?Zemel, Urtasun, Fidler (UofT)CSC 411: 03-Classification12 / 24
GeometrywT x 0 a line passing though the origin and orthogonal to wwT x w0 0 shifts it by w0Figure from G. ShakhnarovichZemel, Urtasun, Fidler (UofT)CSC 411: 03-Classification13 / 24
Learning Linear ClassifiersLearning consists in estimating a “good” decision boundaryWe need to find w (direction) and w0 (location) of the boundaryWhat does “good” mean?Is this boundary good?We need a criteria that tell us how to select the parametersDo you know any?Zemel, Urtasun, Fidler (UofT)CSC 411: 03-Classification14 / 24
Loss functionsClassifying using a linear decision boundary reduces the data dimension to 1y (x) sign(w0 wT x)What is the cost of being wrong?Loss function: L(y , t) is the loss incurred for predicting y when correctanswer is tFor medical diagnosis: For a diabetes screening test is it better to have falsepositives or false negatives?For movie ratings: The ”truth” is that Alice thinks E.T. is worthy of a 4.How bad is it to predict a 5? How about a 2?Zemel, Urtasun, Fidler (UofT)CSC 411: 03-Classification15 / 24
Loss functionsA possible loss to minimize is the zero/one loss(0 if y (x) tL(y (x), t) 1 if y (x) 6 tIs this minimization easy to do? Why?Zemel, Urtasun, Fidler (UofT)CSC 411: 03-Classification16 / 24
Other Loss functionsZero/one loss for a classifier(L0 1 (y (x), t) 0 if y (x) t1 if y (x) 6 tAsymmetric Binary Loss αLABL (y (x), t) β 0if y (x) 1 t 0if y (x) 0 t 1if y (x) tSquared (quadratic) lossLsquared (y (x), t) (t y (x))2Absolute ErrorLabsolute (y (x), t) t y (x) Zemel, Urtasun, Fidler (UofT)CSC 411: 03-Classification17 / 24
More Complex Loss FunctionsWhat if the movie predictions are used for rankings? Now the predictedratings don’t matter, just the order that they imply.In what order does Alice prefer E.T., Amelie and Titanic?Possibilities:III0-1 loss on the winnerPermutation distanceAccuracy of top K movies.Zemel, Urtasun, Fidler (UofT)CSC 411: 03-Classification18 / 24
Can we always separate the classes?If we can separate the classes, the problem is linearly separableZemel, Urtasun, Fidler (UofT)CSC 411: 03-Classification19 / 24
Can we always separate the classes?Causes of non perfect separation:Model is too simpleNoise in the inputs (i.e., data attributes)Simple features that do not account for all variationsErrors in data targets (mis-labelings)Should we make the model complex enough to have perfect separation in thetraining data?Zemel, Urtasun, Fidler (UofT)CSC 411: 03-Classification20 / 24
MetricsHow to evaluate how good my classifier is? How is it doing on dog vs no-dog?Zemel, Urtasun, Fidler (UofT)CSC 411: 03-Classification21 / 24
MetricsHow to evaluate how good my classifier is?Recall: is the fraction of relevant instances that are retrievedR TPTP TP FNall groundtruth instancesPrecision: is the fraction of retrieved instances that are relevantP TPTP TP FPall predictedF1 score: harmonic mean of precision and recallF1 2Zemel, Urtasun, Fidler (UofT)P ·RP RCSC 411: 03-Classification22 / 24
More on MetricsHow to evaluate how good my classifier is?Precision: is the fraction of retrieved instances that are relevantRecall: is the fraction of relevant instances that are retrievedPrecision Recall CurveAverage Precision (AP): mean under the curveZemel, Urtasun, Fidler (UofT)CSC 411: 03-Classification23 / 24
Metrics vs LossMetrics on a dataset is what we care about (performance)We typically cannot directly optimize for the metricsOur loss function should reflect the problem we are solving. We then hope itwill yield models that will do well on our datasetZemel, Urtasun, Fidler (UofT)CSC 411: 03-Classification24 / 24
Multi-class classi cation: multiple possible labels . We are interested in mapping the input x 2Xto a label t 2Y In regression typically Y Now Yis categorical Zemel, Urtasun, Fidler (UofT) CSC 411: 03-Classi cation 5 / 24 . Classi cation as Regression Can we do this task using what we have learned in previous lectures? Simple hack .
9. cot(3 7x) dx; cot u du ln sin u C ln sin(3 7x) C u3 7x du 7 dx ''Äœœœ ” œ kk k k "" "77 7 10. csc( x 1) dx; csc u ln csc u cot u C ux1 du dx ''1 1 1 Äœ œ ” œ † kk du 11 " ln csc( x 1) cot( x 1) Cœ " 1 kk11 11. e csc e 1 d ; csc u du ln csc u cot
Introduction of Chemical Reaction Engineering Introduction about Chemical Engineering 0:31:15 0:31:09. Lecture 14 Lecture 15 Lecture 16 Lecture 17 Lecture 18 Lecture 19 Lecture 20 Lecture 21 Lecture 22 Lecture 23 Lecture 24 Lecture 25 Lecture 26 Lecture 27 Lecture 28 Lecture
CSC 8301: Lecture 12 Linear Programming CSC 8301- Design and Analysis of Algorithms Lecture 12 Linear Programming (LP) 4 LP – Shader Electronics Example The Shader Electronics Company produces two products: 1.Eclipse, a portable touchscreen digital player; it takes 4 hours of electronic work and 2 hours in the assembly shop; it sells for a
Part No Description Page 411 72 10-01 Washer G 411 75 00-08 Needle bar K 411 75 03-02 Screw K 411 75 04-01 Screw K 411 78 10-03 Lamp A, K 411 96 68-01 Screw A, D,K,P,R
70-411 Author: edusum.com Subject: MCSA Windows Server 2012 Keywords: 70-411 PDF, 70-411 VCE, 70-411 Dumps, 70-411 Questions, Microsoft Administering Windows Server 2012 Dumps, MCSA Windows Server 2012 Certification Questions Created Date: 12/18/2018 9:05:13 PM
Guarantee All Exams 100% Pass One Time! 70-411 Dumps 70-411 Exam Questions 70-411 PDF 70-411 VCE http://www.braindump2go.com/70-411.html
To increase the power rating of the CSC without degrading the utilization of power semiconductor devices, a novel multilevel CSC, named the parallel-cell multilevel CSC, is proposed. Based on a six-switch CSC cell, the parallel-cell multilevel CSC has the advantages of high power rating, low harmonics, fast dynamic response and modularity.
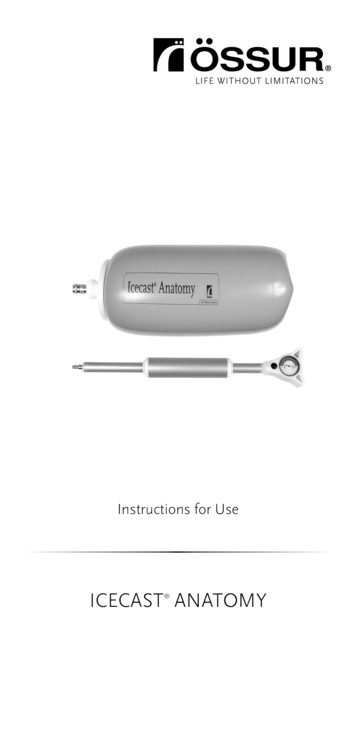
The Icecast Anatomy pressure casting system allows the clinician to produce a reliable, repeatable and well-fitting TSB socket. DESIGN Icecast Anatomy is a single chamber pressure casting system, which provides pressure to shape the soft tissue. The single chamber pressure system is designed to provide optimal pressure distribution. The chamber is reinforced with matrix, for durability and to .