SEISMIC: A Self-Exciting Point Process Model For .
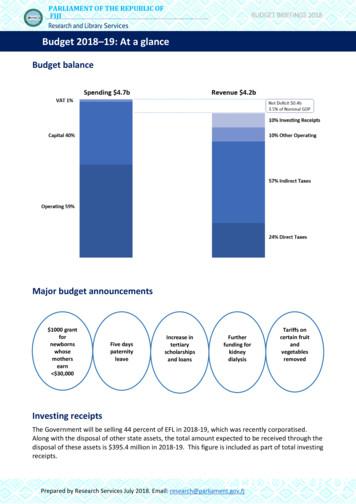
SEISMIC: A Self-Exciting Point Process Modelfor Predicting Tweet PopularityQingyuan ZhaoMurat A. ErdogduHera Y. HeStanford UniversityStanford UniversityStanford he1@stanford.eduAnand RajaramanJure LeskovecStanford UniversityStanford uABSTRACTSocial networking websites allow users to create and share content.Big information cascades of post resharing can form as users ofthese sites reshare others’ posts with their friends and followers.One of the central challenges in understanding such cascading behaviors is in forecasting information outbreaks, where a single postbecomes widely popular by being reshared by many users.In this paper, we focus on predicting the final number of resharesof a given post. We build on the theory of self-exciting point processes to develop a statistical model that allows us to make accurate predictions. Our model requires no training or expensive feature engineering. It results in a simple and efficiently computableformula that allows us to answer questions, in real-time, such as:Given a post’s resharing history so far, what is our current estimateof its final number of reshares? Is the post resharing cascade pastthe initial stage of explosive growth? And, which posts will be themost reshared in the future?We validate our model using one month of complete Twitter dataand demonstrate a strong improvement in predictive accuracy overexisting approaches. Our model gives only 15% relative error inpredicting final size of an average information cascade after observing it for just one hour.Categories and Subject Descriptors: H.2.8 [Database Management]: Database applications—Data miningGeneral Terms: Algorithms; Experimentation.Keywords: information diffusion; cascade prediction; self-excitingpoint process; contagion; social media.1.INTRODUCTIONOnline social networking services, such as Facebook, Youtube,and Twitter, allow their users to post and share content in the formof posts, images, and videos [9, 17, 21, 30]. As a user is exposedto posts of others she follows, the user may in turn reshare a postwith her own followers, who may further reshare it with their respective sets of followers. This way large information cascades ofpost resharing spread through the network.Permission to make digital or hard copies of all or part of this work for personal orclassroom use is granted without fee provided that copies are not made or distributedfor profit or commercial advantage and that copies bear this notice and the full citation on the first page. Copyrights for components of this work owned by others thanACM must be honored. Abstracting with credit is permitted. To copy otherwise, or republish, to post on servers or to redistribute to lists, requires prior specific permissionand/or a fee. Request permissions from Permissions@acm.org.KDD’15, August 10-13, 2015, Sydney, NSW, Australia.c 2015 ACM. ISBN 978-1-4503-3664-2/15/08 . 15.00.DOI: http://dx.doi.org/10.1145/2783258.2783401.A fundamental question in modeling information cascades is topredict their future evolution. Arguably the most direct way to formulate this question is to consider predicting the final size of aninformation cascade. That is, to predict how many reshares a givenpost will ultimately receive.Predicting the ultimate popularity of a post is important for content ranking and aggregation. For instance, Twitter is overflowingwith posts and users have a hard time keeping up with all of them.Thus, much of the content gets missed and eventually lost. Accurate prediction would allow Twitter to rank content better, discovertrending posts faster, and improve its content-delivery networks.Moreover, predicting information cascades allows us to gain fundamental insights into predictability of collective behaviors whereuncoordinated actions of many individuals lead to spontaneous outcomes, for example, large information outbreaks.Most research on predicting information cascades involves extracting an exhaustive set of features describing the past evolutionof a cascade and then using these features in a simple machinelearning classifier to make a prediction about future growth [4, 6,17, 20, 26, 30]. However, feature extraction can be expensive andcumbersome, and one is never sure if more effective features couldbe extracted. The question remains how to design a simple andprincipled bottom-up model of cascading behavior. The challengelies in defining a model for an individual’s behavior and then aggregating the effects of the individuals in order to make an accurateglobal prediction.Present work. Here we focus on predicting the final size of an information cascade spreading through a network. We develop a statistical model based on the theory of self-exciting point processes.A point process indexed by time is called a counting process whenit counts the number of instances (reshares, in our case) over time.In contrast to homogeneous Poisson processes which assume constant intensity over time, self-exciting processes assume that all theprevious instances (i.e., reshares) influence the future evolution ofthe process. Self-exciting point processes are frequently used tomodel “rich get richer” phenomena [22, 23, 33, 36]. They are idealfor modeling information cascades in networks because every newreshare of a post not only increases its cumulative reshare count byone, but also exposes new followers who may further reshare thepost.We develop S EISMIC (Self-Exciting Model of Information Cascades) for predicting the total number of reshares of a given post.In our model, each post is fully characterized by its infectiousnesswhich measures the reshare probability. We allow the infectiousness to vary freely over time in agreement with the observation thatthe infectiousness can drop as the content gets stale (see Figure 1).
Retweet CountHistogram of Retweet Times75502500246Infectiousness Estimated by n by SEISMIC20000Retweets150001000050000024Time since original tweet (hour)TruthSEISMICLR6ObservedFigure 1: First 6 hours of retweeting activity of a populartweet [1] (top). The controversial tweet is about the fresh deathof dictator Muammar Gaddafi and mentions singer JustinBieber. Interestingly, the car manufacturer Chevrolet Twitteraccount inappropriately retweeted the tweet about 30 minutesafter the original tweet, which possibly lead to tweet’s sustainedpopularity. Tweet infectiousness against time as estimated byS EISMIC (middle). Predictions of the tweet’s final retweet count(denoted as “Truth”) as a function of time (bottom). We compare S EISMIC with time series linear regression (LR), “Observed” plots the cumulative number of observed retweets by agiven time. Notice S EISMIC quickly finds an accurate estimateof the tweet’s final retweet count.Moreover, our model is able to identify at each time point whetherthe cascade is in the supercritical or subcritical state, based onwhether its infectiousness is above or below a critical threshold.A cascade in the supercritical state is going through an “explosion”period and its final size cannot be predicted accurately at the current time. On the contrary, a cascade is tractable if it is in subcritical state. In this case, we are able to predict its ultimate popularityaccurately by modeling the future cascading behavior by a GaltonWatson tree.Our S EISMIC approach makes several contributions: Generative model: S EISMIC imposes no parametric assumptions and requires no expensive feature engineering. Moreover, as complete social network structure may be hard to obtain, S EISMIC assumes minimal knowledge of the network:The only required input is the time history of reshares andthe degrees of the resharing nodes. Scalable computation: Making a prediction using S EISMIConly requires computational time linear in the number of observed reshares. Since predictions for individual posts can bemade independently, our algorithm can also be easily parallelized. Ease of interpretation: For an individual cascade, the modelsynthesizes all its past history into a single infectiousness parameter. This infectiousness parameter holds a clear meaning, and can serve as input to other applications.We evaluate S EISMIC on one month of complete Twitter data,where users post tweets which others can then reshare by retweeting them. We demonstrate that S EISMIC is able to predict the final retweet count of a given tweet with 30% better accuracy thanthe state-of-the-art approaches (e.g., [12]). For reasonably popular tweets, our model achieves 15% relative error in predicting thefinal retweet count after observing the tweet for 1 hour, and 25%error after observing the tweet for just 10 minutes. Moreover, wealso demonstrate how S EISMIC is able to identify tweets that willgo “viral” and be among the most popular tweets in the future. Bymaintaining a dynamic list of 500 tweets over time, we are able toidentify 78 of the 100 most reshared tweets and 281 of the 500 mostreshared tweets in just 10 minutes after they are posted.The rest of the paper is organized as follows: Section 2 surveys the related work. Section 3 describes S EISMIC, and Section 4shows how the model can be used to predict the final size of aninformation cascade. We evaluate our method and compare its performance with a number of baselines as well as state-of-the-art approaches in Section 5. Last, in Section 6, we conclude and discussfuture research directions.2.RELATED WORKThe study of information cascades is a rich and active field [27].Recent models for predicting size of information cascades are generally characterized by two types of approaches, feature based methods and point process based methods.Feature based methods first extract an exhaustive list of potentially relevant features, including content features, original posterfeatures, network structural features, and temporal features [6]. Thendifferent learning algorithms are applied, such as simple regressionmodels [2, 6], probabilistic collaborative filtering [35], regressiontrees [3], content-based models [24], and passive-aggressive algorithms [26]. There are several issues with such approaches: laborious feature engineering and extensive training are crucial for theirsuccess, and the performance is highly sensitive to the quality ofthe features [4, 30]. Such approaches also have limited applicability because they cannot be used in real-time online settings—giventhe massive amount of posts being produced every second, it ispractically impossible to extract all the necessary features for everypost and then apply complicated prediction rules. In contrast, S EIS MIC requires no feature engineering and results in an efficientlycomputable formula that allows it to predict the final popularity ofmillions of posts as they are spreading through the network.The second type of approach is based on point processes, whichdirectly models the formation of an information cascade in a network. Such models were mostly developed for the complementaryproblem of network inference, where one observes a number of information cascades and tries to infer the structure of the underlyingnetwork over which the cascades propagated [8, 10, 13, 14, 15, 18,33, 36]. These methods have been successfully applied to study thespread of memes on the web [10, 14, 32, 33] as well as hashtags on
Symbolwptφ(s)itiniRtR NtNteλtp̂tR̂ (t)DescriptionPost/information cascadeInfectiousness of w at time t (Section 3.2)Memory kernel (Section 3.1)Node that contributed ith reshare.i 0 corresponds to the originator of the post.Time of the ith reshare relative to the original post.Out-Degree of the ith nodeCumulative popularity by time t: {i 0; ti t} Final popularity (final number of reshares):P {i 0} Cumulative degree of resharers by time t: i:ti t niEffective cumulativeR t degree of resharers by time t:P tφ(s ti )dsnNte Rii 0tiIntensity of cumulative popularity RtModel’s estimate of infectiousness pt at time tModel’s estimate at time t of final popularity R the network. We consider that the time s between the arrival ofa post in a users’ timeline and a reshare of the post by the useris distributed with density φ(s). The probability density φ(s) isalso called a memory kernel because it measures a physical/socialsystem’s memory of stimuli [7].The distribution of human response time φ(s) has been shown tobe heavy-tailed in social networks [5]. Usually the tail of φ(s) isassumed to follow a power-law with exponent between 1 and 2 ora log-normal distribution [7, 34]. However, due to the rapid natureof information sharing on Twitter, it is also natural to expect manyinstant reaction times. In fact, our exploratory data analysis in Section 5.2 confirms that in Twitter, φ(s) is approximately constant forthe first 5 minutes and then followed by a power-law decay. Different social networks may have different distributions of humanreaction times. However, φ(s) only needs to be estimated once pernetwork and thus we can safely assume it is given. We describe adetailed estimation procedure of φ(s) in Section 5.2.Table 1: Table of symbols.3.2Twitter [36]. In contrast, our goal is not to infer the network but topredict the ultimate size of a cascade in an observed network.A major distinction between our model and existing methodsbased on Hawkes processes (e.g., [22, 23, 33, 34, 36]) is that weassume the process intensity λt depends on another stochastic process pt , the post infectiousness. In other words, we allow the infectiousness to change over time. Moreover, some of these methods [34] rely on computationally expensive Bayesian inference,while our method has linear time complexity. Another recentlyproposed related work is [12], which also takes the point processapproach and directly aims to predict tweet popularity. However,their method makes restrictive parametric assumptions and does notconsider the network struct
SEISMIC: A Self-Exciting Point Process Model for Predicting Tweet Popularity Qingyuan Zhao Stanford University qyzhao@stanford.edu Murat A. Erdogdu Stanford University erdogdu@stanford.edu Hera Y. He Stanford University yhe1@stanford.edu Anand Rajaraman Stanford University anand@cs.stanford.edu Jure Leskovec Stanford University jure@cs.stanford .
The Seismic Tables defined in Pages 5 & 6 are for a seismic factor of 1.0g and can be used to determine brace location, sizes, and anchorage of pipe/duct/conduit and trapeze supports. The development of a new seismic table is required for seismic factors other than 1.0g and must be reviewed by OSHPD prior to seismic bracing. For OSHPD,
EXAMPLE 9 SEISMIC ZONE 1 DESIGN 1 2018 Design Example 9 Example 9: Seismic Zone 1 Design Example Problem Statement Most bridges in Colorado fall into the Seismic Zone 1 category. Per AASHTO, no seismic analysis is required for structures in Zone 1. However, seismic criteria must be addressed in this case.
SC2493 Seismic Technical Guide, Light Fixture Hanger Wire Requirements SC2494 Seismic Technical Guide, Specialty and Decorative Ceilings SC2495 Seismic Technical Guide, Suspended Drywall Ceiling Construction SC2496 Seismic Technical Guide, Seismic Expansion joints SC2497 Seismic
Peterson, M.D., and others, 2008, United States National Seismic Hazard Maps ․ Frankel, A. and others, Documentation for the 2002 Update of the National Seismic Hazard Maps ․ Frankel, A. and others, 1996, National Seismic Hazard Maps Evaluation of the Seismic Zoninig Method ․ Cornell, C.A., 1968, Engineering seismic risk analysis
To develop the seismic hazard and seismic risk maps of Taungoo. In developing the seismic hazard maps, probabilistic seismic hazard assessment (PSHA) method is used. We developed the seismic hazard maps for 10% probability of exceedance in 50 years (475 years return period) and 2 % probability in 50 years (2475 years return period). The seisic
This analysis complied with these provisions by using the USGS 2014 National Seismic Hazard Map seismic model as implemented for the EZ-FRISK seismic hazard analysis software from Fugro Consultants, Inc. For this analysis, we used a catalog of seismic sources similar to the one used to produce the 2014 National Seismic Hazard Maps developed by .
the seismic design of dams. KEYWORDS: Dam Foundation, Probabilistic Seismic Hazard Maps, Seismic Design 1. INTRODUCTION To perform seismic design or seismic diagnosis, it is very important to evaluate the earthquake hazard predicted for a dam site in order to predict earthquake damage and propose disaster prevention measures. There are two .
Seismic hazard parameters are estimated and mapped in macro level and micro level based on the study area. The process of estimating seismic hazard parameters is called seismic . maps of Indian Regions earlier, based on several approaches. This includes probabilistic seismic hazard macrozonation of Tamil Nadu by Menon et al. (2010), Seismic .