Real Analysis Description Of Analysis
Real AnalysisMichael Boardman, Pacific University(Chair).Ted Odell, The University of Texas at AustinKyeong Hah Roh, Arizona State UniversityKenneth Ross, University of OregonKaren Saxe, Macalester CollegeDescription of AnalysisThe area of undergraduate analysis includes introductory and advanced courses. First coursesfocus on analysis on the real line including properties of real numbers, basic point-set topology,and the theory of single variable calculus. At some larger institutions, the introductory analysiscourse is offered at several different levels, to allow well-prepared students to advanceimmediately through the material, and less-prepared students more time to navigate the topics.Advanced courses in analysis include topics such as measure theory, Lebesgue integration, metricspace theory, functional analysis, and complex analysis. Most programs offer at least the coursesin introductory analysis and complex analysis. Analysis courses are considered among the mostdifficult courses in the mathematics curriculum. Some courses in analysis are the first higherlevel mathematics courses students take. The logic, even in introductory courses, is much moresophisticated than what students have encountered in previous courses of calculus andintroduction to proof. Finally, the introductory analysis course is the first course in whichstudents undertake the serious study of sequences and series of functions, and for many students itis the first serious study of sequences and series of constants.Student AudienceIt is standard that undergraduate mathematics majors, including majors intending a career in highschool teaching, complete at least one course in introductory analysis, though some programs donot require this. Given the applicability of the results and methods of analysis to most areas ofmathematics, we recommend that an introductory course in analysis be required of or at leaststrongly recommended to all mathematics majors. Many departments report physics, economicsand computer science majors as audiences for their courses. Some engineering students also takethese introductory courses in analysis. More advanced analysis courses typically enroll onlythose students intending graduate study in mathematics or in some cases economics.HistoryThe topics covered in most introductory analysis courses have not changed significantly in atleast the past 30 years. While there are dozens of available new textbooks for the course, many ofthe textbooks that were popular in the 1980s are still in use today (e.g. Rudin, (2)), some withadditional authors and updates. Some programs offer more advanced courses in analysis thatinclude topics such as measure theory and functional analysis, material that had been the purviewof graduate mathematics programs. The primary mode of delivery for introductory coursesappears to be lecture with class discussion. However, the approach is varied with someinstitutions creating student-centered environments such as inquiry-based learning.Use of technologyTools such as graphing calculators and computer algebra systems can improve studentunderstanding of convergence, continuity, and differentiability, and can illustrate interesting casesìï x n sin(1/ x) x ¹ 0such as f (x) íîï 0x 0being a function that is1n -1 times differentiable.
There are readily available Java applets that provide visualizations of the d - definition of limit.Appropriate integration of such resources can help students gain deeper understanding of thecomplicated definitions and results in real analysis.PrerequisitesAt most institutions, the first course in analysis requires completion of the standard singlevariable calculus sequence and at least one “transitions” course that introduces students tomethods of proof. A background in proof including an introduction to quantified statements,proofs by contradiction, contraposition, and mathematical induction, is extremely helpful tostudents working with the multiply-quantified statements that abound in analysis (e.g., “for every, there exists d 0 , . . .”). However, at some institutions Introductory Real Analysis orAdvanced Calculus is used as the first introduction to proof course. Some textbooks are carefullyand deliberately written to serve this purpose (See Lay (1) or Zorn (2), for examples). Whenintroductory analysis is used as the topic for a first proofs course, the scope of the course isusually narrowed when compared to an introductory analysis course that has a proofs course asprerequisite.With few exceptions, higher-level analysis courses require the introductory analysis course as aprerequisite.Cognitive goals addressedAn introductory analysis course typically focuses on the rigorous development of properties ofthe set of real numbers, and the theory of functions on the real line. This includes the study of thetopology of the real numbers, sequences and series of real numbers, continuity, sequences offunctions, differentiability, and Riemann integration. While the specific content of this course isimportant, of equal importance is helping students develop their analytical reasoning and criticalthinking skills. Students must be creative in analysis, and must learn to persevere in solvingcomplicated problems. They should develop the ability to read, understand, and write proofs, andto accurately and concisely communicate mathematics.To understand concepts including limits, convergence of sequences and series, subsequences, thecompleteness ofin contrast with the setof rational numbers, and definitions of thederivative and the Riemann integral, students must grapple with infinite processes. They mustbecome comfortable with imagining things that are difficult to visualize. Students must thinkcreatively to achieve this. Working with the delta-epsilon definition of limit is one of the majorstumbling blocks to student success in the course. Constructing delta-epsilon proofs oftenrequires the student to work backwards: they first identify their target (what they need toconclude in their proof), work backwards toward what they know (their hypotheses), and thenreverse these steps to write a logical proof that is clear, concise, and correct. All of this takesdeep thought, organization, creativity, and careful analysis.Communicating mathematics, both in written and verbal form, should be integral to any analysiscourse. Analysis proofs are sophisticated and students must develop strong communication skillsto successfully write and communicate them. An introductory analysis class is the perfect settingfor students to begin learning to write carefully about mathematics and to present their proofs totheir peers. It is also an ideal time to introduce students to professional mathematical typesettingprograms such as LaTeX. In many ways, the first course in analysis introduces students to theprofession of mathematics.2
Student-centered courses (for example, inquiry based learning, problem based learning, MooreMethod) tend to focus more on these general skills than lecture-based courses, but sometimescover fewer topics. In any case, class enrollment limits should be small enough to assure eachstudent is given the opportunity to develop these skills.Other Mathematical Outcomes Students should demonstrate understanding and facility with proof techniques includingdirect proof, proof by contradiction, and proof by contraposition. Students should improve both written and oral mathematical communication skills. Students should learn the mathematics that forms the rigorous foundation of calculus of asingle real variable. They should develop facility with the major theorems of calculus. In order to help them understand the ideas better, students should be able to constructappropriate examples and counterexamples. To this end, the course should present thestudents with statements whose veracity is in doubt and asked to determine whether ornot those statements are true. Among the topics typically included in a first course in analysis, students should have anunderstanding ofo Properties of sets of real numbers including open and closed sets, density andcompactness,o Sequences and series of real numbers, the definition of convergence, Cauchysequences, limit theorems (such as the monotone convergence theorem), andrelationships between the topology of the real line and sequences (such as theHeine-Borel theorem)o Functions of a real variable, including continuity, differentiability and importanttheorems (e.g. intermediate-value theorem, mean-value theorem),o Sequences and series of functions of a real variable, pointwise convergence,uniform convergence, power series and Taylor series,o Riemann integration and the fundamental theorem of calculus.o The historical development of the theory of analysis.Ideal CourseThe ideal course in introductory analysis should help students understand the underpinnings ofcalculus and to prepare them to dive further into important topics such as measure and probabilitytheory, metric and normed linear spaces, differential geometry, and functional analysis, and toprepare for advanced excursions in differential equations.Students in this course should learn to work independently, to read and understand theorems, andto construct their own arguments and explain them to others. The course should also introducestudents to mathematical writing.3
Sample Course SyllabiIntroductory AnalysisThe following are suggested themes and topics for a standard one-semester course in introductoryanalysis that has a proofs-based prerequisite. Topics marked with # can be considered optionaltopics to include given sufficient time. We list the themes and topics in one logical order, butthere are other orders in which these topics can be covered. For example, some may coverintegration before covering series of functions and function approximation. Properties of the real numberso Completenesso Open and closed setso Properties of absolute valueo Supremum and infimum of a setSequences and series of real numberso Limit of a sequenceo Convergence of bounded monotone sequenceso Subsequences and the Bolzano-Weierstrass theoremo Cauchy sequenceso Series convergenceo Tests for convergenceo Absolute convergence versus conditional convergence and correspondingpropertiesMore topology of the real lineo Compactnesso The Heine-Borel theoremo Dense setso The Baire category theorem #Functions on the real lineo Continuity Continuity and compact sets The extreme value theorem Uniform continuity The intermediate value theorem Lipschitz continuity #o Differentiability Properties of differentiable functions Darboux’s Theorem and the intermediate value property of derivatives Fermat’s Theorem and the location of extrema for a differentiablefunction The mean value theoremo Functions illustrating important ideas, for example Nowhere continuous functions Functions that are differentiable but with a discontinuous derivative Continuous nowhere differentiable functionsSequences of functionso Pointwise convergenceo Uniform convergence and its relationship with continuityo Weierstrass M-testSeries of functions and function approximation4
o Power serieso Taylor serieso Fourier Series #o Bernstein polynomials and Weierstrass approximation #o Lagrange interpolating polynomials #Riemann integrationo Criteria for integrabilityo Properties of the Riemann integralo Uniform convergence and integration (when can the limit move inside theintegral)o The fundamental theorem of integral calculusMetric spaces #o Topology of metric spaces #o Equivalent metrics #o Completeness #o Continuous mappings between metric spaces #Normed linear spaces #o Topology of normed linear spaces #o Equivalent norms #o Completeness #o Continuous mappings between normed linear spaces #Introduction to Lebesgue Measure #5
Introductory Analysis with Introduction to ProofThe following are suggested themes and topics for a one-semester course in introductory analysisthat does not have a proofs-based prerequisite. Topics marked with # can be considered optionaltopics to include given sufficient time. We list the themes and topics in one logical order, butthere are other orders in which these topics can be covered. Logic, connectives, quantifiersSet notation and operationsProof techniqueso Direct proofo Inductive proofso Proof by contradictionFunctionsCardinalityProperties of the real numberso Completenesso Open and closed setso Properties of absolute valueo Supremum and infimum of a setSequences and series of real numberso Limit of a sequenceo Convergence of bounded monotone sequenceso Subsequences and the Bolzano-Weierstrass theoremo Cauchy sequenceso Series convergenceo Tests for convergenceo Absolute convergence versus conditional convergence and correspondingpropertiesMore topology of the real lineo Compactnesso The Heine-Borel theoremo Dense setso The Baire category theorem #Functions on the real lineo Continuity Continuity and compact sets The extreme value theorem Uniform continuity The intermediate value theoremo Differentiability Properties of differentiable functions Darboux’s Theorem and the intermediate value property of derivatives Fermat’s Theorem and the location of extrema for a differentiablefunction The mean value theoremo Functions illustrating important ideas, for example Nowhere continuous functions Functions that are differentiable but with a discontinuous derivative Continuous nowhere differentiable functions6
Sequences of functionso Pointwise convergenceo Uniform convergence and its relationship with continuityo Weierstrass M-testSeries of functions and function approximation #o Power series #o Taylor series #o Fourier Series #o Bernstein polynomials and Weierstrass approximation #o Lagrange interpolating polynomials #Riemann integration #o Criteria for integrability #o Properties of the Riemann integral #o Uniform convergence and integration (when can the limit move inside theintegral) #o The fundamental theorem of integral calculus #7
Introductory Analysis based on Fourier SeriesThe following are suggested themes and topics for a one-semester course in introductory analysisthat is built around Fourier series and that has a proofs-based prerequisite. We list the themes andtopics in one logical order, but there are other orders in which these topics can be covered. Fourier series: what they are, why they are important, why they are problematicInfinite sequences and series of constantso Limit of a sequenceo Convergence of bounded monotone sequenceso Subsequences and the Bolzano-Weierstrass theoremo Cauchy sequenceso Series convergenceContinuity, differentiability, mean value theorem, properties of Ro Completenesso Open and closed setso Compactnesso Continuity and compact setso The extreme value theoremo Uniform continuityo The intermediate value theoremo Properties of differentiable functionso Darboux’s Theorem and the intermediate value property of derivativeso Fermat’s Theorem and the location of extrema for a differentiable functiono The mean value theoremConvergence Testso Absolute convergence versus conditional convergence and correspondingpropertiesUniform Convergence and its implicationso Sequences of functionso Pointwise and uniform convergenceo Uniform convergence and the relationship to continuityo Uniform convergence and the relationship to term-by-term differentiationRiemann Integrationo Criteria for integrabilityo Properties of the Riemann integralo Uniform convergence and integration (when can the limit move inside theintegral)o The fundamental theorem of integral calculus8
BibliographyRemark: The presence of a text on this list is not meant to imply an endorsement of thattext, nor is the absence of a particular text from the list meant to be an antiendorsement. The texts are chosen to illustrate the sorts of texts that support varioustypes of real analysis courses. Please note that some of the articles listed were writtenby authors of this report.Texts Referenced in Report1. Lay, Steven R. Analysis: With an Introduction to Proof. 5th. ed, Pearson, 2012.2. Rudin, Walter. Principles of Mathematical Analysis. 3rd. ed, McGraw Hill, 1976.3. Zorn, Paul. Understanding Real Analysis. CRC Press, 2010.Specific Tasks or Activities4.Amstrong, G. M. Some projects for calculus and analysis. Problems, Resources, andIssues in Mathematics Undergraduate Studies, 1(3), 275-286, 1991.This paper suggests some project appropriate for real analysis students. Project Icompares concepts of calculus with the development of infinitesmals. Project II definesthree additional types of derivatives and compare them with the ordinary derivative.Project III contrasts integral of Newton, Cauchy, and Riemann. The author providedresults of class testing the project.5. Barnes, J. Teaching real analysis in the land of make believe. Problems, Resources, andIssues in Mathematics Undergraduate Studies, 17(4), 366-372, 2007.This article introduced the authors experience of teaching mathematical definitions in astandard introductory real analysis. The definitions covered in this article are those ofconvergent sequences, bounded sequences, Cauchy sequences, continuous functions,removable discontinuity, and uniform continuity. Fairy tales describing a few of thedefinitions in detail were suggested as reading materials to help students understandthese definitions.6.Barnes, J. Feather boas in real analysis. Problems, Resources, and Issues in MathematicsUndergraduate Studies, 21(2), 130-141, 2011.This article described a collection of hands-on activities using feather boas, yarn, anddoorknob hangers to help students understand the formal definitions for convergentsequences, continuity, and uniform continuity.7.Mamona-Downs, J. Letting the intuitive bear on the formal: A didactical approach forthe understanding of the limit of a sequence. Educational Studies in Mathematics, 48,259-288, 2001.This article provides an analysis of the formal definition of limit via identifying roles ofeach symbol that occurs to achieve a mental image firmly consonant with the definitionand a description of how this mental imagery may be used to reexamine the validity ofsome intuitive beliefs. The author also provided a series of tasks to encourage students’intuitive images of a sequence as having an ultimate term associated with the limit.9
8. Mamona-Downs, J. On introducing a set perspective in the learning of limits of realsequences. International Journal of Mathematical Education in Science and Technology,41(2), 277-291, 2010.This article aimed to provide students with opportunities to contrast the convergentbehavior of a sequence and the accumulation points of the underlying set of the sequencethrough their commonalities and differences in structure. The author claims that themore set-oriented perspective provides students with an alternative source for provingpropositions concerning properties of the limit of a sequence. Some examples were givenand comments were made on the cognitive level in this article.9.Roh, K. How to help students conceptualize the rigorous definition of the limit of asequence. Problems, Resources, and Issues in Mathematics Undergraduate Studies, 20(6),473-487, 2010a.This article presented how real analysis students can be guided to conceptualize therigorous definition of the limit of a sequence. In particular, this article proposed a handson activity, called the ε-strip activity, with a physical device made from translucent paper,as an instructional method to help students understand what it means for a sequence tohave a limit via visualization of the ε-N definition of the limit of a sequence. Twostatements were suggested to students, each of which was written in terms of arelationship between ε and N, similar to the ε-N definition: One required infinitely manypoints of the sequence in the ε-strips, which students commonly suggest, but is notcompatible with the standard definition. The other required only finitely many pointsoutside the ε-strips, which sounds counterintuitive to students, but is logically equivalentto the standard definition. This article also describes the learning objectives of each stepof the activity, and provides detailed instructional methods to guide students to reach thelearning objectives.10. Roh, K., & Y.-H Lee, The Mayan activity: A way of teaching multiple quantifications inlogical contexts. Problems, Resources, and Issues in Mathematics Undergraduate Studies,21(8), 685-698, 2011.This article suggests an instructional intervention to help students understand statementsinvolving multiple quantifiers in real analysis contexts. The authors first focused onstudents’ mis-interpretations of multiple quantifiers related to the ε-N definition of thelimit of a sequence and pointed out that they resulted from a lack of understanding of thesignificance of the order of the quantifiers in the definition. Next, the authors introducedthe Mayan activity which was designed to cause and then to help students resolve theircognitive dissonance. In particular, the Mayan stonecutter story in the activity waspresented in an understandable and colloquial form so that students can recognize theindependence of ε from N in the ε-N definition. The authors illustrate how the Mayanactivity can be used in classroom as a useful instructional intervention for student tostudy proofs of convergent sequences and Cauchy sequences.Students’ Understanding or Perspectives11. Dawkins, P. Metaphor as a possible pathway to more formal understanding of thedefinition of sequence convergence. The Journal of Mathematical Behavior, 31(3), 331343, 2012.10
This article presented how an instructor’s introduction of a metaphor constituted anexperientially real context in which an undergraduate real analysis students developed aproperty-based definition of sequence convergence. The author traced the transformationof the student’s conception from non-standard, personal concept definition rooted in themetaphor to a concept definition for sequence convergence compatible with the standarddefinition. This study also documented the student’s progression through the definition-ofand definition-for stages of mathematical activity in an interactive lecture classroomcontext.12. Edwards, B. Undergraduate mathematics majors’ understanding and use of formaldefinitions in real analysis. Unpublished doctoral dissertation, The Pennsylvania StateUniversity, 1997.The focus of the study was on undergraduate mathematics majors’ understanding and useof formal definitions in real analysis. This thesis includes a case-study analysis and across-case analysis which focused on students’ understanding of the role of mathematicaldefinitions and the logical and conceptual complexities of such definitions as those forpointwise continuity, absolute continuity, infinite decimals, and connectedness. Theauthor found that students did not necessarily share mathematicians’ understanding ofthe role of mathematical definitions as lexical, and they had difficulties with thecomplexities of wording and logic, especially in the continuity definitions. Also, ifstudents settled prematurely on the meaning of all or part of a given definition theyseemed to be unable or unwilling to consider conflicting evidence.13. Roh, K. Students' images and their understanding of definitions of the limit of a sequence.Educational Studies in Mathematics, 69, 217-233, 2008.The author explored how students’ images of limit influence their understanding ofdefinitions of the limit of a sequence. In a series of task-based interviews, studentsevaluated the propriety of statements describing the convergence of sequence through aspecially designed hands-on activity, called the ε-strip activity (Roh, 2010a). Inparticular, this paper illustrates how students’ understanding of definition of the limit ofa sequence can be influenced by their images of limits as asymptotes, cluster points, ortrue limit points. The implications of the study for the teaching and learning of theconcept of limit are also discussed in this paper.14. Roh, K. An empirical study of students' understanding of a logical structure in thedefinition of limit via the ε-strip activity. Educational Studies in Mathematics, 73, 263279, 2010b.This study provided empirical evidence that students’ understanding of the limit of asequence is closely related to their understanding of a logical structure in defining thelimit of a sequence. The subjects of the study were college students who had alreadyencountered the concept of limit and limit symbols, but did not have any experience withrigorous proofs using the ε-N definition. The author addressed three essentialcomponents that students must conceptualize in order to understand properly therelationship between ε and N in the ε-N definition of limit: The index N corresponding toε should be determined before completing the variation of ε, any ε in the definitionimplies the arbitrariness of error bounds, and the arbitrariness of ε implies that the errorbound decreases towards 0.11
15. Swinyard, C., Reinventing the formal definition of limit: The case of Amy and Mike.Journal of Mathematical Behavior, 30, 93-114, 2011.This article focused on the evolution of the students’ definition of limit in ten-weekteaching experiment. Two students, neither of whom had previously seen the conventional𝜀 𝛿 definition of limit, reinvented a formal definition of limit capturing the intendedmeaning of the conventional definition. This article provided a detailed account of howstudent might think about limits formally.16. Swinyard, C., & S. Larsen, Coming to understand the formal definition of limit:Insights gained from engaging students in reinvention. Journal for Research inMathematics Education, 43(4), 465-493, 2012.This article illustrates a model of how student might come to understand the concept ofthe limit of a function at a point and at infinity, respectively. Analyzing two teachingexperiments, the authors proposed two theoretical constructs to account for the students’success in formulating and understanding the formal definition of the limit of a function:(1) the need for students to move away from their tendency to attend first the inputvariable of the function; and (2) the need for students to overcome the practicalimpossibility of completing an infinite process.Instructional Techniques or Classroom Structures17. Alcock, L., Interactions between teaching and research: Developing pedagogical contentknowledge for real analysis. In R. Leikin & R. Zazkis (Eds.), Learning through teachingmathematics: Development of teachers’ knowledge and expertise in practice (pp. 227245). DOI: 10.1007/978-90-481-3990-3 12, 2010.This chapter describes the author’s five practices used in teaching undergraduate realanalysis: regular testing on definitions, tasks that involve extending example spaces,tasks that involve constructing and understanding diagrams, use of resources forimproving proof comprehension and tasks that involve mapping the structure of a wholecourse. The author describes the rationale for each of these practices from a teacher’spoint of view and relate each to results from mathematics education research, focusingon the need for students to develop skills on multiple levels and the question of how bestto use available lecture time.18. Dawkins, P., Concrete metaphors in the undergraduate real analysis classroom. In S. L.Swars, D. W. Stinson, & S. Lemons-Smith (Eds.) Proceedings of the 31st Annual Meetingof the North American Chapter of the International Group for the Psychology ofMathematics Education, (5, pp. 819-826), Atlanta, Georgia: Georgia State University,2009.The author examined metaphors that an instructor used in a real analysis classroom, andclassified them into logical and mathematical metaphors. Logical metaphors were thoseused to clarify the logical structure of a definition and perhaps guide a proof structure.Mathematical metaphors were those used to demonstrate aspects of the conceptsthemselves or the structure of the definitions. The instructor’s teaching methods inDawkins’ study were different from “definition-theorem-proof” instruction in the sensethat the instructor involved students in choosing definitions or theorems and ingenerating examples, arguments, and counter-examples. The teaching methods were also12
different from all-student-discovery styles in the sense that the instructor always gave theclass guidance and introduced formal mathematical knowledge (definitions andtheorems) once the students arrived at the underlying ideas of the formal mathematicalknowledge. The article reported that instructional metaphors were likely to be integratedinto the students’ concept images, and were likely used for recall, integrated into studentlanguage, and potentially introduce misconceptions.19. Dawkins, P., & K. Roh, Mechanisms for scientific debate in real analysis classrooms. InWeist, L. & Lamberg, T. (Eds.), Proceedings of the 33rd Conference of the NorthAmerican Chapter of the International Group for the Psychology of MathematicsEducation (pp. 820-828), Reno, NV: University of Nevada, Reno, 2011.This article presents two accounts of successful scientific debate from differentundergraduate, real analysis classrooms by combining observations from separateinstances of non-traditional, inquiry-oriented real analysis instruction. The first realanalysis class was taught at a mid-sized, research university in the spring of 2009. Amathematician who specialized in differential geometry taught the first real analysiscourse. This article illustrated one day of the first course leading up to the definition ofthe limit of a function at a point, in which the instructor presented examples that did anddid not have limits due to restricted domains so as to motivate the standard requirementthat limits only be defined at cluster points of the domain of the function. On the o
Advanced courses in analysis include topics such as measure theory, Lebesgue integration, metric space theory, functional analysis, and complex analysis. Most programs offer at least the courses in introductory analysis and complex analysis. Analysis courses are considered among
1.1 Hard Real Time vs. Soft Real Time Hard real time systems and soft real time systems are both used in industry for different tasks [15]. The primary difference between hard real time systems and soft real time systems is that their consequences of missing a deadline dif-fer from each other. For instance, performance (e.g. stability) of a hard real time system such as an avionic control .
asics of real-time PCR 1 1.1 Introduction 2 1.2 Overview of real-time PCR 3 1.3 Overview of real-time PCR components 4 1.4 Real-time PCR analysis technology 6 1.5 Real-time PCR fluorescence detection systems 10 1.6 Melting curve analysis 14 1.7 Passive reference dyes 15 1.8 Contamination prevention 16 1.9 Multiplex real-time PCR 16 1.10 Internal controls and reference genes 18
the model, we hope to overcome the barriers that currently exist in applying real options analysis (ROA) to real estate development, and provide developers with a tool to help them better understand the rewards associated with real options. Real options analysis is an important topic in real estate due to the nature of the development environment.
Real-Time Analysis 1EF77_3e Rohde & Schwarz Implementation of Real -Time Spectrum Analysis 3 1 Real-Time Analysis 1.1 What “Real-Time” Stands for in R&S Real-Time Analyzers The measurement speed available in today's spectrum analyzers is the result of a long
Real -time Real -life O riented DSP Lab Modules Abstract: In this p aper , we present a sequence of engaging lab exercises that implement real -time real -life signal/data acquisition, analysis, and processing using MatL ab , LabV iew, and NI myDAQ. Examples of these signals include real -time human voice and music signals.
Document revision 1.10 (June 22, 2007, 16:49 GMT) This document applies to MikroTik RouterOS V3.0 Table of Contents Table of Contents Summary Description System Backup Description Command Description Example Example Exporting Configuration Description Command Description Example Importing Configuration Description Command Description Example .
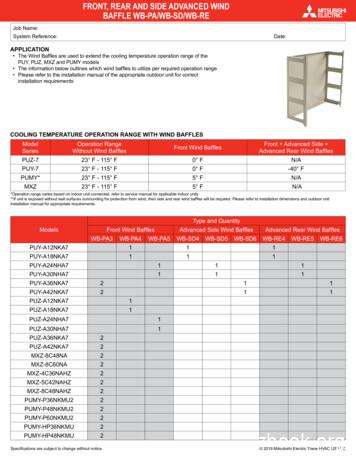
mitsubishi electric wind baffle - wb-pa3 mr. slim p-series pumy-60 submittal wb-pa3 description description c description d description e description f description g description proprietary and confidential the information contained in this drawing is the sole property
real estate investing 3 8 17 26 37 45 53 63 72 introduction by shelly roberson and david s. roberson, esq. the world of real estate investing educating yourself in real estate niches and strategies for real estate investment creating an effective business plan locating investment properties financing real estate investments real estate .