Mecanique - BTS
1/50MECANIQUEA- MECANIQUE (présentation)1. Système mécanique matérielCorps solide indéformable ou ensemble de corps auxquels on s’intéresse.2. Référentiel2A. référentiel espaceRepère d’espace O, i, j , k .Système d’axes lié à la terre.Le choix d’un repère permettra une mise en équation simple.(1) repère héliocentrique ( S , i, j , k ), galiléen*Sera galiléen, tout référentiel qui a un mouvementde translation rectiligne et uniforme par rapport à (1).(2) repère géocentrique ( T , i, j , k )Sur une courte durée (T1 à T2), le mouvementd’un solide est pratiquement rectiligne uniforme.Ce n’est plus le cas sur une longue durée (T1 à T3).(2) est considéré comme galiléen sur une courte duréemalgré que son mouvement ne soit pas unetranslation rectiligne uniforme très rigoureux.De plus le référentiel terrestre tourne autour de l’axe des pôles, mais celle-ci peut être négligée sur unecourte durée (quelques minutes)*Galilée (1564-1642), physicien et astronome italien, fondateur des raisonnements de la mécanique,.2B. référentiel tempsOrigine des temps et unité de temps.3. STATIQUE3A. définitionEtude des conditions pour lesquelles un corps est immobile.A l’instant initial t 0, le corps est immobile.
2/503B. conditions d’équilibrea- Forces Fextérieures 0La somme des forces extérieures appliquées au corps est nulle.b- Moments MF extérieures 0 ou MF extérieures / 0La somme vectorielle des moments des forces extérieures par rapport à un point quelconque est nulle,ou la somme algébrique des moments des forces extérieures par rapport à l’axe est nulle.3C. applicationsProjetés sur les trois axes, ces deux équations donnent six équations algébriques indépendantes.(au plus six inconnues)En général, F 0 sera projetée sur deux axes contenus dans un plan, où se trouvent les forcesextérieures, et M F / 0 sera projetée sur un axe perpendiculaire à ce plan.Au total, trois équations algébriques (trois inconnues).Exemple :Solide sur un plan horizontal, sur un plan incliné,.(avec ou sans frottements)Arc-boutement, échelle, potence, console,.4. MOUVEMENT4A. exemplesUn corps aura un mouvement de translation quand tous les points ont la même trajectoire et la mêmevitesse.Un corps aura un mouvement de rotation autour d’un axe , quand chaque point a une trajectoirecirculaire centrée sur l’axe.Exemples :- mouvement rectiligne (la trajectoire est une droite)- mouvement circulaire (la trajectoire est un cercle)- mouvement curviligne (la trajectoire est une courbe)- mouvement sinusoïdal, rectiligne ou circulaire, (élongation, vitesse et accélération varient« sinusoïdalement »).
3/504B. CINEMATIQUEEtude du mouvement d’un corps dans son rapport avec le temps, sans se préoccuper des causes.On parlera : repère, temps, position, vitesse et accélération.4C. DYNAMIQUEa- définitionEtude du mouvement d’un corps connaissant les forces extérieures qui lui sont appliquées.On établira les relations fondamentales : Fextérieuresb- Forces m.aa : accélération (m.s-2)m : masse du corps kg)c- Moments MF extérieures / J .d 2αdt 2d 2α: accélération angulaire (rad.s-2)dt 2J : moment d’inertie du corps (kg.m2) MF extérieures / : somme algébrique des moments des forces extérieures par rapport àl’axe de rotation pour un solide en rotation autour d’un axe fixe (N.m)5. Définitions et relations5A. point matérielSolide de masse m, pouvant être assimilé à un point.5B. solide parfaitIl a une masse constante.Il ne subit aucune déformation.
4/505C. moment d’inertie J d’un solideSolide en rotation autour d’un axe fixe .Energie cinétique du solide :nn11Ec mi .vi2 ω 2 mi .Ri22 i 1i 1 21Ec J .ω 22ω (rad.s-1)nJ mi .Ri2i 1R, rayon (m)m, masse (kg)J (kg.m2)Point matérielJ M.R2Anneau circulaireJ M.R2Cylindre creuxJ M.R2Disque1J M.R22Cylindre plein1J M.R22Sphère2J M.R255D. accélérationVariation de la vitesse en intensité.Positive et constante, la vitesse augmente (mouvement uniformément accéléré).Négative et constante, la vitesse décroit (décélération) (mouvement uniformément décéléré).Nulle, vitesse uniforme (le vecteur vitesse peut varier en conservant la même intensité).5E. action mécanique et vecteur-forceOn appelle force, toute action mécanique capable :- de modifier l’état de repos ou l’état de mouvement d’un corps.- de déformer un corps.- de compenser d’autres actions mécaniques.L’action mécanique est modélisée par un VECTEUR-FORCE qui a pour caractéristiques :- point d’application- direction- sens- intensité (newton, N), norme, valeur, module.Exemples :- action mécanique de contact- action mécanique à distance (champ de pesanteur, champ électrique, champ magnétique).- force extérieure : elle est crée par un corps situé à l’extérieur du solide.
5/505F. moment d’une force par rapport à.a.un point OM F OA F OA.F.sinα(grandeur vectorielle)b.un axe Δ M F / F .d(grandeur algébrique, N.m)
6/505G. travail a- d’une forceWAF extérieure F . AB F . AB.cos αB
7/50b- d’une force appliquée à un solide en rotationdW F .dl F .dl F .R.dαdW M F / .dααα00W dW M F / dαWαF extérieure M F / .αc- d’un couple de moment constantF1 F2 FM C / F .dWC M C .α5H. énergiesa- pesanteur1Energie mécanique (constante) Energie cinétique ( m.v 2 ) Energie potentielle de pesanteur ( m.g .h )2
8/50b- ressortxdynamique11Energie mécanique (constante) Energie cinétique ( m.v 2 ) Energie potentielle élastique ( k .x 2 )22statiquec- solide en rotationEc 1J .ω 225I. puissance a d’une forcePmoyenne FA BW t t : temps pour la force pour aller de A vers BW F dW F .dldl F . F .v t 0 t 0 tdtdtdtPins tan tan ée F .v F .V .cos α ( Pi F .v, si α 0 )Pins tan tan ée lim Pmoyenne limb d’une force appliquée à un solide en rotation ou d’un coupleWPm tW dW M .dαdαPi lim Pm lim M. M .ω t 0 t 0 tdtdtdtPi M .ω
9/506. PorteDans chaque situation, préciser « l’effet »de la force sur son immobilisme ou sa rotation.1. M F / 0 et M F ' / 0113. M F / 024. M F / F3 .d35. F F2 F3'M F / M F / M23F' / M F / F3 .a F ' .d36. F F1 F F1 F2 F3'M F / M F / M F / M123F' / M F / F3 .a F ' .d3
10/50B- STATIQUE1. Conditions d’équilibre d’un solide1A. Forces Fextérieures 0La somme des forces extérieures qui lui sont appliquées est nulle.Ces forces seront, en général coplanaires.En projetant la relation sur deux axes (Ox et Oy) orthogonaux, on obtient deux équations.(S’il n’y a que trois forces, leurs droites d’action concourent en un même point)Exemples de forces : poids, réaction, tension,.1B. Moments MF / 0 La somme algébrique des moments des forces extérieures par rapport à l’axe est nulle.On obtient une équation.Ce qui fait trois équations, qui nous permettent de trouver trois inconnues au maximum.On utilise parfois M F 0 , la somme vectorielle des moments des forces par rapport à un pointquelconque est nulle.2. Résolution d’un problèmea) Bien repérer le solide en équilibre.b) Bien repérer les forces extérieures à ce solide.c) Bien lire l’énoncé pour, en fonction du nombre d’inconnue(s).1, 2, 3 ou plus et ainsi choisir leséquations qui conviennent, en précisant l’axe choisi si nécessaire.3. ExercicesExercice 1 : Le solide repose sur un plan horizontal.1) Sans frottement :Quelles sont les forces mises en jeu ?2) Avec frottement :Même question si on exerce une action sur ce solide.Préciser :- les conditions de glissement- l’angle de frottement- le coefficient de frottement de glissement- le cône d’équilibre.3) L’arc-boutement :Quelle condition doit-on avoir pour que l’on ait toujours équilibre ?
11/50Exercice 2 : Le solide repose sur un plan incliné.1) Sans frottement.a- Quelles sont les forces mises en jeu sur ce solide ?b- Exprimer littéralement les intensités R et T en fonction deP, θ et .β.(données : m 10 kg ; θ 23 ; AB 1,10 m ; AG 13 cmg 9,81 m.s-2)c- Connaissez-vous une autre méthode pour trouver ce résultat ?2) Avec frottement.a- Préciser pour quel angle θ on a équilibre.(on désigne par k le coefficient de frottement de glissementqui se développe au contact du solide et du plan incliné)b- Si θ 30 et k 0,3, l’équilibre est-il possible ?c- Exprimer F en fonction de m, g, θ et φ à l’équilibre.d- Que se passe-t-il si θ φ ?3) Avec frottement.a- Exprimer T en fonction de P, θ, β, et φ l’angle de frottementà l’équilibre.b- Calculer T.(données : P 1000 N ; θ 10 ; β 25 et φ 18 )c- Pour quelle valeur de β, T est-elle minimale ?Exercice3 : potenceOn considère une potence constituée d’une barrehomogène AB (longueur ℓ1 3,50 m et intensitédu poids P1 200 N) et d’un câble horizontal(longueur ℓ2 2,00 m et de poids négligeabledevant la tension).1) Calculer l’intensité de la tension du câble.2) Donner les caractéristiques de la réaction dusupport en A.Exercice 4 : tableau accroché1) Montrer que le point d’attache A, à l’arrière du tableaudoit être situé à une distance déterminée du point le plusbas du tableau.2) Evaluer en fonction de ℓ1 et ℓ2 l’angle β que fait letableau avec la verticale.3) En déduire que ℓ2 est comprise entre deux valeurs quel’on exprimera en fonction de ℓ1.
12/50Exercice 5 : ConsoleVérifier que :1) .la barre AC est soumise à une traction dont oncalculera l’intensité.2) .la barre AB est soumise à une compression donton calculera l’intensité.(les barres ont des poids négligeables devant les forces)Exercice 6 : ConsoleOn désire étudier les efforts aux liaisons dans la console.On dispose d’une barre AB horizontale de longueur ℓ et d’une4barre CD oblique de longueur ℓ .3Le poids des deux barres est négligeable.1) Calculer les efforts en B, C et D.2) Vérifier ce résultat par une construction graphique.Exercice 7 : Console mobileElle est constituée d’un triangle rectangle isocèle ABC, de poidsnégligeable devant la charge P portée sur AC.(AB AC ℓ)Elle est installée sur un tuyau de diamètre d 2 r.Soit k le coefficient de frottement de glissement entre laconsole et le tuyau.Calculer la distance minimale x à l’axe du tuyau pour laquellela charge P peut être supportée sans qu’il y ait glissementde la console.Exercice 8 : Echelle simple1) Sur parois lissesa- échelle seuleMontrer que si les contacts se font sans frottement, il est impossible d’appuyerobliquement contre un mur vertical. (soit P le poids de l’échelle)b- échelle avec filDans les exemples exprimer la réaction en A et B, ainsi que la tension du filen fonction de P, ℓ et θ.
13/502) Sur sol rugueuxa- Calculer l’angle de frottement φ pour maintenir juste l’échelle en équilibre.En déduire les réactions en A et B.(ℓ 5 m, P 250 N et θ 30 )b- Le poids de l’échelle étant négligeable, quelle est la condition pour que l’homme de poidsP1 1000 N, monte jusqu’en haut de l’échelle ?Si θ 30 , calculer la hauteur maximale à laquelle l’homme peut monter sans que l’échelle ne glisse.c- Même question, le poids de l’échelle n’est plus négligeable (P2 250 N).d- Même question, quand le contact en A est rugueux.Exercice 9 : Echelle doubleSur sol lisse, avec un homme dessus en G.Elle est constituée de deux échelles simples articulées en O,de longueur ℓ et de même poids p 100 N.Il n’y a aucun frottement en O, A et B.L’homme a un poids P 900 N.Calculer les intensités :F4/1 ; F4/2 ; F3/2 et F1/2.Exercice 10 : Sphère1) Démontrer qu’une sphère ne peut pas être enéquilibre sur un plan incliné.2) Une sphère homogène de poids d’intensité P 30 Nrepose sans frottement sur deux plans.Calculer l’intensité des réactions RA et RB exercéespar les supports en A et B, l’allongement du ressortétant de 30 mm.Exercice 11 : Barre homogèneElle est en équilibre, calculer la réaction en O.(ℓ 10 m ; P 100 N et AO 3 m)Exercice 12 :Un solide de centre de gravité G, peut tourner autour d’un axe de rotation passant par O.Expliquer les trois sortes d’équilibre, en positionnant O.- stable- indifférent- instable
14/50Exercices divers 13 :1)Un solide de masse m 4 kg est suspendueà deux cordes.1) Exprimer P, T1 et T2 en fonction de θ.2) Les calculer pour θ 50 .2) FermeUne ferme supportée en A un poids d’intensité 3000 N.1) Calculer les réactions en B et C.2) Vérifier que les barres sont soumises chacune à une compression et que la barre BC est soumiseà une traction.3) Calculer les intensités de ces dernières en supposant que le poids des barres est négligeable devantles autres forces et que les contacts en B et C sont sans frottement.
15/50C- CINEMATIQUE : position, vitesse et accélération1. Vecteur position1A. trajectoireM est la position du point à l’instant t.M (x, y, z) : coordonnées cartésiennes.La trajectoire représente l’ensemble des positions occupées par le point M.1B. vecteurOM x.i y. j z.kOM OM x OM y OM zOM x 2 y 2 z 21C. équations horaires et cartésienne du mouvement de M- dans l’espace : x f(t) , y g(t) et z h(t)- dans le plan : x f(t) et y g(t)- rectiligne : x f(t)Sauf exception, l’étude portera sur des mouvements plans.Equations horaires du mouvement plan de M : x f(t) et y g(t)Equation cartésienne : y f(x)2. Vecteur vitesse2A. vitesse moyenneEntre les instants t1 et t2 : vm M 1M 2t2 t1M1M 2t2 t1M 1M 2 OM 2 OM 1 et t2 t1 tvm
16/502B. vitesse instantanéeà l’instant t1.vt1 lim t 0vt1 M 1M 2OM 2 OM 1 OM lim lim t 0 t 0t2 t1 t tdOM ddxdidydj ( x.i y. j ) .i .x . j .ydtdtdtdtdtdt00vt1 xɺ.i yɺ. j vx .i v y . j( xɺ vx et yɺ v y : dérivées premières )v vx2 v y23. Vecteur accélération3A. accélération moyenneEntre les instants t1 et t2.am v2 v1 v t2 t1 tam v t3B. accélération instantanéea- coordonnées cartésiennesà l’instant t1. dOM d dt d 2 OM d 2 xd2y v d v at1 lim .i .j t 0 tdtdtdt 2dt 2dt 2dv ydvat1 x .i . j ɺɺx.i ɺɺy. j ax .i a y . jdtdt( ɺɺx ax et ɺɺy a y : dérivées sec ondes )a ax2 a y2en coordonnées cartésiennes
17/50L’accélération instantanée at1 se décompose en deux composantes (tangentielle et normale) :b- accélération tangentielleaTaT dvdtc- accélération normalev2RR : rayon de courbure de la trajectoire au pointaNaN d- représentation et valeursdv.tdtElle est orientée dans le sens du mouvement, quand v augmente.Elle est orientée en sens inverse du mouvement, quand v diminue.dv 0 ).Elle est nulle quand v est constante (dt1) aT v2.nRElle est nulle quand le mouvement est rectiligne.Elle est non nulle dans tous les autres mouvements (circulaire,.).2) aN a aT2 aN2en coordonnées curvilignesExercice 1 :Un point mobile M, se déplace dans un plan muni d’un repère cartésien (Ox, Oy).On a choisi un instant origine.t2Les lois horaires du mouvement sont, en unités S.I : x et y 1 t 2 .21) Marquer quelques positions occupées par M pendant l’intervalle de temps [0 s ; 1 s].(Echelle : 6,4 cm pour 1 m sur Ox et 5 cm pour 1 m sur Oy)2) a-Déterminer l’équation cartésienne de la trajectoire dans le repère (Ox, Oy).b- Quelle est la nature de ce mouvement ?3) a- Déterminer le vecteur vitesse et le vecteur accélération de M, à un instant quelconque.b- Que peut-on dire du vecteur accélération ?c- Représenter ces vecteurs sur le graphique, en précisant l’échelle choisie.4) Déterminer la vitesse et l’accélération de m à la date t 0,5 s.5) Quelle est la nature (de façon plus précise) de ce mouvement ?
18/50D- CINEMATIQUE : exemples de mouvements1. Résolution des exercicesPour la recherche de l’équation horaire du mouvement, l’application des lois va nous conduireaux coordonnées de l’accélération.On va ensuite devoir remonter jusqu’aux coordonnées du vecteur position.dérivée premièredérivée sec onde 2Afonction : A.t 2 B.t C 2 A.t B primitiveprimitive(les constantes B et C seront déterminées par les conditions initiales du mouvement)2. Mouvement rectiligne uniformev1 v2 v3Conditions initiales : t 0 ; OM 0 x0 .i ; v v.iv constante et a 0A l’instant t : OM x.i ; v v.iEquation horaire du mouvement : x f(t)1position : A.t 2 B.t C vitesse : A.t B accélération : A2position :x v.t x0 vitesse :v accélération : 0a 0v constantex v.t x0 (x0 : position initiale) x2 – x1 v.(t2 – t1)x (m) ; v (m.s-1) ; a (m.s-2)Exercice 2 :Un entrepreneur de bâtiment a loué une grue pour le levage de panneaux lors d’une construction deMOB.La position du centre d’inertie G du panneau est repéré sur un axe vertical orienté vers le haut.La flèche de la grue est située à une hauteur h 21 m.Le panneau repose sur le sol.Au bout de quatre secondes, à une hauteur de 1,6 m, G s’élève avec un mouvement rectiligne uniformeà la vitesse de 0,8 m.s-1 pendant 15 s.1) Ecrire et déterminer les équations horaires du mouvement.2) Quelle est la hauteur du panneau à la fin de cette phase de montée ?3) Représenter (échelles au choix) les diagrammes des vitesses v g(t) et des espaces x f(t).
19/503. Mouvement circulaire uniformeLa vitesse v varie : v1 v2 v3 .Son intensité reste constante : v1 v2 v3 v.dv 0dtdvv2aT 0 et aN a dtRC’est un mouvement accéléré : accélération centripète constante.2π1C’est un mouvement périodique de période T (f )ωTdα αɺ ).et de vitesse angulaire ω.constante (dt(α ω t ; ω en rad.s-1 et α en rad)a Le point M peut être repéré par :1) ses coordonnées cartésiennes (x,y) dans le repère ( O, i, j ).2) son abscisse curviligne : s AM α .R .()3) son abscisse angulaire : α OA, OM .x R.cos αy R.sin αdxdyvx xɺ ω.R.sin ωt et v y yɺ ω.R.cos ωtdtdtetv vx2 v y2 ω 2 .R 2 ω.Rax ɺɺx ω 2 .R.cos ωt et a y ɺɺy ω 2 .R.sin ωta ax2 a 2y ω 4 .R 2 ω 2 .REquation horaire du mouvement : α f(t)1 2A.t B.t C vitesse : A.t B accélération : A2position angulaire : α αɺ .t α 0 vitesse angulaire : αɺ accélération angulaire : 0 αɺɺposition :1TAbscisse angulaire : α ω.t α0 (α0 : abscisse initiale) α2 – α1 ω.(t2 – t1)ω ( αɺ ): vitesse angulaire constante (rad.s-1)α : abscisse angulaire (rad)2πω 2π . fTAccélération angulaire : αɺɺ 0Période T (s) ; Fréquence f (Hz) : f Abscisse curviligne : s α.RVitesse linéaire constante v (m.s-1) : v ω.Rv2-2Accélération centripète constante a (m.s ) : a ω 2 .RR
20/50Exercice 3 :Un moteur actionne un cylindre qu’il fait tourner à la vitesseangulaire constante de 20 tr.min-1.Sur ce cylindre, de rayon R 10 cm, s’enroule un câbleinextensible, tendu à l’une de ses extrémités par une chargequ’il entraîne.Ce câble ne glisse pas sur le cylindre.1) Quelle est la nature du mouvement de M, ainsi que celui de N.2) Déterminer pour N :la vitesse angulaire en rad.s-1, la vitesse enm.s-1 et l’accélération centripète en m.s-2.3) Déterminer l’accélération et la vitesse de M.Exercice 4 :Un point a une trajectoire circulaire de rayon R.Son vecteur accélération centripète est a 50 m.s-2.1) Montrer que le mouvement est uniforme.2) La période du mouvement est T 0,4π s, quel est le rayon du cercle trajectoire ?4. Mouvement rectiligne uniformément variéa constantea constanteConditions initiales : t 0 ; OM 0 x0 .i ; v0 v0 .i ; a a.iA l’instant t : OM x.i ; v v.i ; a a.iEquation horaire du mouvement : x f(t)1position : A.t 2 B.t C vitesse : A.t B accélération : A21x a.t 2 v0 .t x0 v a.t v0 a2a constantev a.t v01x a.t2 v0.t x0 (x0 : position initiale et v0 : vitesse initiale)2mouvement accéléré : a et v sont de même sensmouvement retardé : a et v sont de sens contrairesv22 v12 2a. ( x2 x1 ) et v2 v1 a. ( t2 t1 ) *t v v0a(21 v v01 v v0 v v0 x x0 a v0 ; x x0 2a2 a a )2 v v0 v0 a 2a. ( x x0 ) ( v v0 ) 2v0 . ( v v0 ) v 2 2v.v0 v02 2v0 .v 2v02 v 2 v022
21/50Exercice 5 :Un solide glisse sur un banc à coussin d’air inclinépar rapport à l’horizontale.On s’intéresse au mouvement d’un point M de ce solide.Ce point reste sur la droite (D) orientée de x’ vers x.De A, on lance le point M à la vitesse vA .vA est un vecteur de même direction et sens que x ' x ,de module v A 0,8 m.s-1.Le mouvement de M est uniformément varié.1) Calculer l’accélération de M, sachant que le mobilerebrousse chemin en B, situé à la distance 1,6 m.2) Quel est le temps mis pour aller de A vers B ?3) A quel endroit le mobile se trouve-t-il cinq secondes après le départ de A ?Exercice 6 :Une locomotive, initialement immobile, démarre sur une voie rectiligne avec une accélérationconstante a 1 m.s-2.Lorsque sa vitesse est 108 km.h-1, elle garde cette vitesse pendant 20 s.1) Quelle distance a-t-elle parcourue au total ?2) Tracer le diagramme des espaces du mouvement, c'est-à-dire la représentation graphiquede la loi horaire.Alors que la locomotive avance à la vitesse de 108 km.h-1, le mécanicien actionne le frein.La décélération est constante et vaut 4 m.s-2.La locomotive parcourt 112,5 m en ligne droite.3) Calculer la durée de ce freinage et la vitesse finale de la locomotive.5. Mouvement circulaire uniformément varié- accélération angulaire : αɺɺ (rad.s-2)- vitesse angulaire : αɺ (ω) (rad.s-1)- abscisse angulaire : α (rad)- abscisse curviligne : s (m)- vitesse linéaire : v (m.s-1)- accélérations linéaires tangentielle et normale : aT et aN (m.s-2)- rayon du cercle trajectoire : R (m)Equation horaire du mouvement : α f(t)1position : A.t 2 B.t C vitesse : A.t B accélération : Ad 2α2αɺɺ 21dtα αɺɺ.t 2 αɺ 0 .t α 0 αɺ αɺɺ.t αɺ 0 αɺɺ2αɺɺ constanteαɺ αɺɺ.t αɺ 01α αɺɺ.t 2 αɺ 0 .t α 0 ( α 0 : abscisse angulaire initiale et αɺ 0 : vitesse angulaire initiale)2 αɺ αɺ12 2αɺɺ. (α 2 α1 ) et αɺ 2 αɺ1 αɺɺ. ( t2 t1 )22s α .Rv αɺ .R ω.Rv2a N ω 2 .R et aT αɺɺ.RR
22/50Exercice 7 :La tête de marteau décrit, dans un plan vertical, un quartde cercle de centre O et de rayon R, pour venir frapperle clou (R 50,0 cm).La position initiale du centre de masse G du marteauest à la verticale du point O.A l’instant t 0, le marteau est dans la position de lafigure et sa vitesse est nulle.L’accélération angulaire constante est αɺɺ 200 rad.s-2.1) Ecrire l’équation horaire angulaire du mouvement,α f(t).2) Calculer la durée jusqu’à l’impact avec le clou.3) Calculer la vitesse angulaire à la fin du mouvementlorsque le marteau frappe le clou.4) Calculer la vitesse linéaire du centre de masse aumoment de l’impact, ainsi que ses accélérationsnormales et tangentielles.αR6. Mouvement rectiligne sinusoïdal (harmonique)x xm.cos(ωt - φ)φ : phase à l’origine, t 0, (rad)ω : pulsation (rad.s-1)ωt - φ : phase à l’instant t (rad)xm : amplitude (m)x : élongation (m)2π 2π . fTf: fréquence (Hz), nombre de périodes par secondeT : période (s)dxv xɺ ω.xm .sin (ω.t ϕ ) )dtdv d 2 xa 2 ɺɺx ω 2 .xm .cos (ω.t ϕ ) ω 2 .xdt dtω x xm.cos (ω.t- φ)v - ω. xm.sin (ω.t- φ)a - ω2.xd 2x2Equation différentielle : 2 ω .x 0dtω 2π 2π . fTLa solution de l’équation différentielle est : x xm.cos (ω.t-φ)
23/50Exercice 8 :Un point matériel, M, animé d’un mouvement rectiligne sinusoïdal, décrit un segment AB.La fréquence du mouvement est f 20 Hz.A la date t 0 ; le mobile passe par le milieu de AB, en se déplaçant de A vers B à la vitesse 0,5 m.s-1.1) Déterminer la loi horaire du mouvement et la longueur du segment AB.2) Quelle est l’accélération algébrique du mobile, lorsqu’il rebrousse chemin en A ?7. Mouvement circulaire sinusoïdal xα (rad)Rxαm mR(ω0 : pulsation)Elongation linéairex xm.cos(ω0.t-φ) α.RVitesse linéairedxv - ω0. xm.sin(ω0 t-φ)dtv ω.R - ω0.R. αm.sin(ω0 t-φ)Accélérationd 2xaT 2 ω02 .xm .cos (ω0 .t ϕ ) ω02 .xdtaT ω02 .R.α m .cos (ω0 .t ϕ ) αɺɺ.RElongation angulaireα α m .cos (ω0 .t ϕ )Vitesse angulairedααɺ ω ω0 .α m .sin (ω0 .t ϕ )dtAccélération angulaired 2ααɺɺ 2 ω02 .α m .cos (ω0 .t ϕ ) ω02 .αdtv2aN ω02 .RREquations différentiellesd 2x ω02 .x 02dtd 2α ω02 .α 02dt2πω0 2π . f 0T0Les solutions de ces équations différentielles sont : x xm.cos(ω0.t-φ) et α α m .cos (ω0 .t ϕ )
24/50E- DYNAMIQUE : lois et principes1. Principe de l’inertieDans un référentiel galiléen, le centre d’inertie (a) d’un solide isolé (b) ou pseudo-isolé (c) a unmouvement rectiligne uniforme (d) ou est immobile (e).a- Point du solide, G. Il est souvent confondu avec le centre de gravité (centre de masse).b- Le solide n’est soumis à aucune force extérieure.c- Le solide est soumis à des forces extérieures telle que F extérieures 0 .d- v G cons tan te .e- v G 0 .2. Principe de l’action et de la réactionLorsqu’un corps (1) exerce sur un corps (2) une action mécanique F 1 2 localisée en B,le corps (2) exerce sur le corps (1) une action mécanique F 2 1 localisée en A.Ces deux forces sont opposées.F 2 1 F 1 2Application : Réaction d’un supportR P
25/503. Relations fondamentales de la dynamique3A. ForcesDans un référentiel galiléen, la somme des forces extérieures appliquées à un solideest égale au produit de la masse du solide par l’accélération de son centre d’inertie. FextérieuresSolide ponctuel : m.a G Fextérieures m.aCette relation ne permet de prévoir que le mouvement du centre d’inertie G, sauf pour le mouvement detranslation.3B. MomentsPour un solide en rotation autour d’un axe fixe Dans un référentiel galiléen, la somme algébrique des moments des forces extérieurespar rapport à l’axe de rotation est égale au produit du moment d’inertie du solide parson accélération angulaire αɺɺ . MF extérieures / J .αɺɺ3C. unitésm (kg); a (m.s-2); F (N); M (N.m); J (kg.m2); αɺɺ d 2α(rad.s-2)dt 24. Théorème de l’énergie cinétiqueDans un référentiel galiléen, la variation de l’énergie cinétique entre l’état final etl’état initial, est égale à la somme des travaux des forces et des travaux des couplesextérieurs au système. EC ECt ECt Wt1F t WC212(théorème utilisé, surtout, pour calculer les vitesses)WAF B F . AB pour la translation et pour la rotationet pour un coupleWαF extérieure M F / .αWC M C .α5. Résolution des exercices1. Définir le système en translation ou en rotation.2. Faire le bilan des forces extérieures appliquées au système.3. Faire un schéma.4. Préciser le référentiel galiléen dans lequel on travaille.Faire le choix d’un repère d’espace et le choix d’un repère de temps.5. Appliquer :a- la relation fondamentale, en la projetant sur des axes (Ox, Oy,.)(ou) b- le théorème de l’énergie cinétique.
26/50F- DYNAMIQUE : exemples de mouvements1. Mouvement d’un solide sur un plan1A. glissement sans frottement(mouvement de translation)Relation fondamentale F P R m.aProjetons cette relation :( )- sur l’axe O, iP1 0 m.aP.sinα m.am.g.sinα m.aa g.sinαThéorème de l’énergie cinétique1 EC EC 2 EC1 m.v 2 02 WF extérieures( )- sur l’axe O, j1m.v 2 m.g .x.sin α2v 2 2 g .x.sin α-P2 R 0R P2 P.cosα1B. glissement avec frottement(mouvement de translation)Le plan est rugueux ( f : force de frottement)1. F P R f m.a( )Projection sur l’axe O, jP1 0 – f m.am.g.sinα – f m.afa g .sin α mMouvement uniformément varié2.1 EC EC 2 EC1 m.v 2 02 WF ext WP WR W f WP 0 f .x WP WR P.h 0 m.g .x.sin α
27/501m.v 2 m.g .x.sin α f .x2f v 2 2. g .sin α .xm 1C. mouvement circulaire uniforme(cycliste, voiture.dans un virage)R : rayon de courbure.G : centre de gravité du système (cycliste vélo) de masse m.L’axe Gx est dirigé vers le centre O de la trajectoire.Pour prendre le virage, le cycliste doit incliner son plan de symétrie d’un angle θ.Sur un sol lisse, la réaction R 0 serait normale au sol, le cycliste déraperait sous l’action de f .La piste doit être inclinée, avec R : réaction inclinée exercée par le sol sur les pneus perpendiculaireau sol.Sur un sol rugueux, θ φ, φ étant l’angle de frottement.v2F : force centripète, d’intensité constante : F m.a m. m.ω 2 .RRCalcul de θ :Loi fondamentale : F P R m.a- projection sur Ox : 0 R.sinθ m.a- projection sur Oy : -P R.cosθ 0- R.sinθ m.a et R.cosθ P m.g tan θ av2 g R.gExercice 1 : (g 9,8 m.s-2)Une automobile a une masse totale de 1 t.La résistance, opposée à l’avancement due aux frottements solides et à la résistance de l’air, équivautà une force d’intensité égale à 500 N.La voiture roule en ligne droite sur une route horizontale à vitesse constante.(On admet que la force de frottement est constante et est toujours présente quand le véhicule est enmouvement)1) Quelle est l’intensité de la force motrice F ?L’automobile roulant à 72 km.h-1 sur une route rectiligne horizontale, le conducteur freine pour l’arrêter.
28/50La voiture s’arrête sur 100 m.2) Déterminer l’intensité de la force de freinage supposée constante.(quand on freine, on admet que le moteur est débrayé. En réalité, le chauffeur rétrograde et le moteurpar « frein moteur » participe au freinage)Après être repartie, l’automobile prend un virage de rayon de courbure R (r) 100 m à la vitesseconstante v 72 km.h-1.Ce virage est relevé d’un angle θ par rapport à l’horizontale,si bien que la réaction du sol est normale au sol.3) Déterminer θ.2. Mouvement d’un solide sur un cylindreExercice 2 :Un petit solide S de masse m, part, pratiquement sans vitesse du sommet A d’un demi-cylindrede rayon r et de centre O, collé sur un plan horizontal.Les frottements sont négligeables.1) Exprimer les vitesses de S, en fonction de r, de l’intensité de la pesanteur g et de θ OA, OS .()2) Donner une expression de l’intensité de la réaction R, en fonction de θ, r, g et m.Lorsque S dépasse une position S0, S décolle du cylindre.3) déterminer cette position.4) Avec quelle intensité de force , F, le solide appuie-t-il sur le demi-cylindre avant d’atteindre S0 ?3. Tension d’un cableLa tension T c’est la force qu’il faudrait appliquer, si on coupe le câble, pour quele solide conserve le mouvement qu’il avait avant la coupure. F P R m.aProjection sur z’z : -P T m.aT m.a m.g
du poids P 1 200 N) et d'un câble horizontal (longueur ℓ2 2,00 m et de poids négligeable devant la tension ). 1) Calculer l'intensité de la tension du câble. 2) Donner les caractéristiques de la réaction du support en A. Exercice 4 : tableau accroché 1) Montrer que le point d'attache A, à l'arrière du tableau
www.wackergroup.com Cut-Off Saws BTS 930-8340 BTS 935-8341 BTS 1030-8339 BTS 1035-7975 REPAIR MANUAL 0118754en 005 0903 0118754 EN
BTS 75V Packages Components BTS 75V/B Center Hung, Double-Acting BTS 75V/H Center Hung, Single-Acting 1. Top Pivot 8062 8062 2. Bottom Arm 7421 7421 3. Spindle 74010 80010 4. Cover Plate 7510 7510 5. Closer and Cement Case BTS 75V BTS 75V BTS 80 Packages Components BTS 80/B Center Hung, Double-Acting BTS 80/H Center Hung, Single-Acting 1. Top .
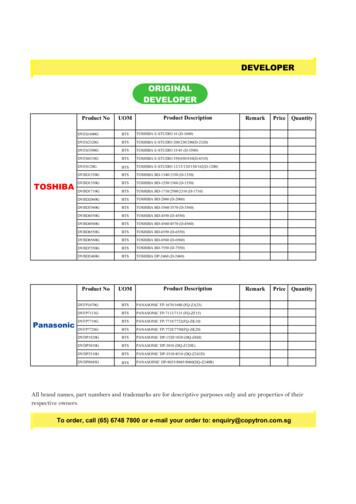
dvbd2460g bts toshiba dp-2460 (d-2460) product no uom remark price quantity dvfp1670g bts panasonic fp-1670/1680 (fq-za25) dvfp7113g bts panasonic fp-7113/7115 (fq-zf15) dvfp7718g bts panasonic fp-7718/7722(fq-zk10) dvfp7728g bts panasonic fp-7728/7750(fq-zk20) dvdp1820g bts panasonic dp-1520/1820 (dq-z60j)
Chapitre 1 : De la mécanique du point vers la mécanique des fluides 1.1 Introduction 1.2 Mécanique du point matériel 1.2.1 Cinématique d‟un point matériel 1.2.2 Dynamique d‟un point matériel 1.3 Mécanique du solide rigide 1.3.1 Cinématique du solide rigide 1.3.2 Dynamique du solide rigide 1.4 Mécanique d‟un milieu continu
The BTS 10200 Softswitch The BTS 10200 Softswitchdelivers software-based * voice call control capabilities in Next Generation IP Service Provider networks. The BTS 10200 softswitchcan provide traditional Class 5 subscriber services and Class 4 trunkingsupport. The BTS 10200 offers a full
(products with factory-fitted hold-open do not carry a CE mark) 2 yes - no 1) For particularly heavy doors and doors which have to close against wind resistance, we recommend the DORMA BTS 80. 78 341 60 51-57 36-42 36-42 2 DORMA BTS 80 DORMA BTS 75 V Floor Springs Whether standard, narrow or wide, whether LH, RH, or single or double action
SECONDE_LMD LA MECANIQUE AU NIVEAU SECONDE Page 1 sur 5 ATTENTION En classe de Seconde on se restreint à la « mécanique du point ». 'est-à-dire que l'on va herher à définir le mouvement d'un o jet massique en étudiant que le mouvement d'un point ien hoisi de et o jet. LA MECANIQUE AU COLLEGE le système solaire
Cisco BTS 10200 Softswitch Release 5.0 07-31-2017 Cisco BTS 10200 Softswitch Release 6.0 07-31-2017 Cisco BTS 10200 Softswitch Release 6.0.3 07-31-2017 Cisco BTS 10200 Softswitch Release 7.0 07-30-2017