Continuous Probability Distributions Uniform Distribution
Continuous ProbabilityDistributionsUniform Distribution
Important Terms & Concepts Learned Probability Mass Function (PMF) Cumulative Distribution Function (CDF) Complementary Cumulative Distribution Function (CCDF) Expected valueMeanVarianceStandard deviation Uniform distributionBernoulli distribution/trialBinomial distributionPoisson distributionGeometric distributionNegative binomial distribution2
Which distribution is this?A.B.C.D.E.UniformBinomialGeometricNegative BinomialPoissonGet your i‐clickers3
Which distribution is this?A.B.C.D.E.UniformBinomialGeometricNegative BinomialPoissonGet your i‐clickers4
Which distribution is this?A.B.C.D.E.UniformBinomialGeometricNegative BinomialPoissonGet your i‐clickers5
Which distribution is this?A.B.C.D.E.UniformBinomialGeometricNegative BinomialPoissonGet your i‐clickers6
Which distribution is this?A.B.C.D.E.UniformBinomialGeometricNegative BinomialPoissonGet your i‐clickers7
Which distribution is this?A.B.C.D.E.UniformBinomialGeometricNegative BinomialPoissonGet your i‐clickers8
Continuous & Discrete RandomVariables A discrete random variable is usually integernumber– N – the number of proteins in a cell– D‐ number of nucleotides different between twosequences A continuous random variable is a real number– C N/V – the concentration of proteins in a cell ofvolume V– Percentage D/L*100% of different nucleotides inprotein sequences of different lengths L(depending on set of L’s may be discrete but dense)Sec 2‐8 Random Variables10
Probability Mass Function (PMF) X – discrete randomvariable Probability MassFunction: f(x) P(X x)– the probability thatX is exactly equal to xProbability Mass Function forthe # of mismatches in 4‐mersP(X 0) P(X 1) P(X 2) P(X 3) P(X 4) 0.65610.29160.04860.00360.0001Σx P(X x) 1.000011
Probability Density Function (PDF)Density functions, in contrast to mass functions,distribute probability continuously along an intervalFigure 4‐2 Probability is determined from the area under f(x) from a to b.Sec 4‐2 Probability Distributions &Probability Density Functions12
Probability Density FunctionFor a continuous random variable X ,a probability density function is a function such that(1)f x 0means that the function is always non-negative. (2) f ( x)dx 1 b(3)P a X b f x dx area under f x dx from a to baSec 4‐2 Probability Distributions &Probability Density Functions13
Histogram approximates PDFA histogram is graphical display of data showing a series of adjacentrectangles. Each rectangle has a base which represents aninterval of data values. The height of the rectangle creates anarea which represents the probability of X to be within the base.When base length is narrow, the histogram approximates f(x) (PDF):height of each rectangle its area/length of its base.Figure 4‐3 Histogram approximates a probability density function.Sec 4‐2 Probability Distributions &Probability Density Functions16
Cumulative Distribution Functions (CDF & CCDF)The cumulative distribution function (CDF)of a continuous random variable X is,F x P X x x f u dufor x (4-3) One can also use the inverse cumulative distribution functionor complementary cumulative distribution function (CCDF) F x P X x f u du for x xDefinition of CDF for a continous variable is the sameas for a discrete variableSec 4‐3 Cumulative Distribution Functions17
Density vs. Cumulative Functions The probability density function (PDF) is thederivative of the cumulative distributionfunction (CDF).dF x dF x f x dxdxas long as the derivative exists.Sec 4‐3 Cumulative Distribution Functions18
Mean & VarianceSuppose X is a continuous random variable withprobability density function f x . The mean orexpected value of X , denoted as or E X , is E X xf x dx(4-4) The variance of X , denoted as V X or 2 , is 2 V X x f x dx 2 x 2 f x dx 2 The standard deviation of X is 2 .Sec 4‐4 Mean & Variance of a ContinuousRandom Variable19
Gallery of UsefulContinuous Probability Distributions
Continuous Uniform Distribution This is the simplest continuous distributionand analogous to its discrete counterpart. A continuous random variable X withprobability density functionf(x) 1 / (b‐a) for a x b(4‐6)Compare todiscretef(x) 1/(b‐a 1)Figure 4‐8 Continuous uniform PDFSec 4‐5 Continuous Uniform Distribution21
Comparison between Discrete &Continuous Uniform DistributionsDiscrete: PMF: f(x) 1/(b‐a 1) Mean and Variance:μ E(x) (b a)/2σ2 V(x) [(b‐a 1)2–1]/12Continuous: PMF: f(x) 1/(b‐a) Mean and Variance:μ E(x) (b a)/2σ2 V(x) (b‐a)2/1222
X is a continuous random variablewith a uniform distributionbetween 0 and 3.What is P(X 1)?A.B.C.D.E.1/41/30InfinityI have no ideaGet your i‐clickers23
X is a continuous random variablewith a uniform distributionbetween 0 and 3.What is P(X 1)?A.B.C.D.E.1/41/30InfinityI have no ideaGet your i‐clickers24
X is a continuous random variablewith a uniform distributionbetween 0 and 3.What is P(X 1)?A.B.C.D.E.1/41/30InfinityI have no ideaGet your i‐clickers25
X is a continuous random variablewith a uniform distributionbetween 0 and 3.What is P(X 1)?A.B.C.D.E.1/41/30InfinityI have no ideaGet your i‐clickers26
Matlab exercise: generate 100,000 random numbers drawnfrom uniform distribution between 3 and 7 plot histogram approximating its PDF calculate mean, standard deviation andvariance
Matlab template: Uniform PDF Stats ?;r2 ? (std(r2));step 0.1;[a,b] hist(r2,0:step:8);pdf e a./sum(a).? (* or /) step;figure; plot(b,pdf e,'ko‐');
Credit: XKCDcomics
Matlab exercise: Uniform PDF Stats 100000;r2 3 (std(r2));step 0.1;[a,b] hist(r2,0:step:8);pdf e a./sum(a)./step;figure; plot(b,pdf e,'ko‐');
Continuous Uniform Distribution This is the simplest continuous distribution and analogous to its discrete counterpart. A continuous random variable Xwith probability density function f(x) 1 / (b‐a) for a x b (4‐6) Sec 4‐5 Continuous Uniform Distribution 21 Figure 4‐8 Continuous uniform PDF
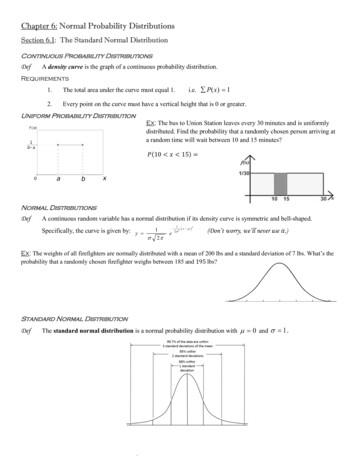
Chapter 6: Normal Probability Distributions Section 6.1: The Standard Normal Distribution Continuous Probability Distributions Def A density curve is the graph of a continuous probability distribution. Requirements 1. 1The total area under the curve must equal 1. i.e. Px 2. Every point
Mar 24, 2014 · Text: A Course in Probability by Weiss 8:4 STAT 225 Introduction to Probability Models March 24, 2014 Whitney Huang Purdue University Uniform and Exponential Distributions Continuous Random Variable Uniform Distribution Exponential Distribution 19.2 Agenda 1 Continuous Random Variable 2 Un
Joint Probability P(A\B) or P(A;B) { Probability of Aand B. Marginal (Unconditional) Probability P( A) { Probability of . Conditional Probability P (Aj B) A;B) P ) { Probability of A, given that Boccurred. Conditional Probability is Probability P(AjB) is a probability function for any xed B. Any
Random variables (discrete and continuous) . concepts from information theory, linear algebra, optimization, etc.) will be introduced as and when they are required (IITK) Basics of Probability and Probability Distributions 2. Random Variables . Uniform: numbers de ned over a xed range Beta: numbers between 0 and 1, e.g., probability of head .
6.1 NORMAL DISTRIBUTION: In probability theory, the normal (or Gaussian) distribution is a very commonly occurring continuous probability distribution—a function that tells the probability that any real observation will fall between any two real limits or real num
Chapter 5: Discrete Probability Distributions 158 This is a probability distribution since you have the x value and the probabilities that go with it, all of the probabilities are between zero and one, and the sum of all of the probabilities is one. You can give a probability distribution
12.7 The Discrete Uniform Distribution 343 12.8 Exercises 346 13 Continuous Random Variables: Uniform and Exponential 349 13.1 The Uniform Distribution 349 13.1.1 Mean and Variance 350 13.1.2 Sums of Uniform Random Variables 352 13.1.3 Examples 354 13.1.4 Generating Random Numbers Uniformly 356 13.2 The Exponential Distribution 357 13.2.1 Mean .
What is artificial intelligence? In their book, ‘Artificial Intelligence: A Modern Approach’, Stuart Russell and Peter Norvig define AI as “the designing and building of intelligent agents that receive percepts from the environment and take actions that affect that environment”.5 The most critical difference between AI and general-