A 10-point Approximating Subdivision Scheme Based On Least Squares .
Available athttp://pvamu.edu/aamAppl. Appl. Math.ISSN: 1932-9466Applications and AppliedMathematics:An International Journal(AAM)Vol. 11, Issue 2 (December 2016), pp. 559 - 575A 10-point Approximating Subdivision SchemeBased on Least Squares TechniqueGhulam Mustafa1 and Muhammad Tahseen Iqbal21Department of MathematicsThe Islamia University of Bahawalpurghulam.mustafa@iub.edu.pk2Department of MathematicsNational College of Business Administration & EconomicsBahawalpur Campustahseeniqbal@hotmail.comReceived: October 16, 2015; Accepted: May 24, 2016AbstractIn this paper, a 10-point approximating subdivision scheme is presented. Least squares techniquefor fitting the polynomial of degree 9 to data is used to develop this scheme. The proposedstrategy can be used to generate a family of schemes. The important characteristics of the schemeare also discussed. Graphical efficiency of the scheme is shown by applying it on different typesof data.Keywords: Approximating subdivision scheme; least squares; regression; polynomial; curvefitting; continuity; local analysis; polynomial generation and reproductionMSC 2010 No.: 93E24, 65D17, 65D07, 65D05, 65D101. IntroductionSubdivision scheme is widely used for curve and surface fitting from few decades. It is analgorithm to define smooth curves and surfaces as a sequence of successively refined controlpolygons. It has an abundant application in the field of science and engineering.559
560G. Mustafa and M.T. IqbalA general form of univariate binary subdivision scheme S which maps polygonf k { fi k }i , k 0 to a refined polygon f k 1 { fi k 1}i is defined in Dyn et al. (1991) by f 2ki 1 2 j fi k j , j k 1k f 2i 1 2 j 1 fi j ,j (1)where the set { j : j } of coefficients is called mask/stencil of the subdivision scheme.The Laurent polynomial of the mask of scheme (1) is defined as ( z ) j z j . A necessaryj condition for the uniform convergence of subdivision scheme defined in Equation (1) is 2 j 1, 2 j 1 1. This is equivalent to ( 1) 0, (1) 2, which impliesj j ( z) (1 z)b( z), b(1) 1. For further reading regarding analysis of the scheme, see Hormann(2012) and Mustafa and Zahid (2013).The subdivision schemes are different due to the different values of ' s. Several techniques havebeen used to find ’s. Deslauriers and Dubuc (1989) and Mustafa et al. (2014) used Lagrangepolynomials to compute ’s while Lian (2009) used wavelet techniques for the computations ofthese values. Costantini and Manni (2010) used Hermite polynomials to generate the values of ' s. One can get 2-point, 3-point, n point schemes from the mask (i.e. the values of 's)obtained from the above techniques. Romani (2015) introduced a class of subdivision schemesby making the variant of existing algorithms. Mustafa et al. (2016) introduced a family ofschemes by convolving the existing schemes. A major advantage of the subdivision schemes isthat they can be easily applied to virtually any data type. However, by Mustafa et al.(2015) earlywork in the subdivision schemes do not deal with noisy data with impulsive noises. Dyn et al.(2015) and Mustafa et al. (2015) pointed out that least squares based subdivision schemes arebetter choices to handle with these types of problems. Therefore, in this paper, we prefer to useleast squares technique instead of other techniques.The method of least squares is one of the golden techniques in statistics for curve fitting. In thismodern era method of least squares is frequently used to find numerical values of the parametersto fit a function to set of data. It means that the overall solution minimizes the sum of the squaresof the errors made in the results of every single equation i.e. the best fitted curve by the leastsquares methods minimizes the sum of squared difference between an observed value and thefitted value provided by a model.Suppose that the data points are (r1 , f r1 ), (r2 , f r2 ), (r3 , f r3 ), ., (rm , f rm ), where ri is the independentvariable, and f ri is the dependent variable. The fitting curve has the deviation (error) from eachdata point, i.e. d1 f r1 r1 , d2 f r2 r2 , d3 f r3 r3 , , dm f rm rm .
AAM: Intern. J., Vol. 11, Issue 2 (December 2016)561mAccording to the techniques of least squares, the best fit curve has the property that R di2 , isr 1minimum.The n point scheme means the scheme takes n consecutive points from the initial polygon tocompute new point in order to get a refined polygon. Here n is called the complexity of thescheme. For example, if the scheme has complexity 10 then it means the scheme uses 10consecutive points from the initial polygon to compute new point to get refined polygon.Mustafa et al. (2015) pointed out that the less complexity, and the very complexity schemes arenot suitable to handle noisy data. Therefore, in this paper, a 10-point approximating subdivisionscheme is constructed by fitting a polynomial of degree 9 with the help of least squarestechnique. The proposed strategy can also be used to generate lower and higher complexityschemes. It can also be used to produce ternary, quaternary, , b-ary schemes b 3 .The paper is organized as follows: In Section 2, a 10-point scheme is introduced. In Section 3,we discuss continuity, polynomial generation, polynomial reproduction, local analysis of thescheme. Applications of the scheme are presented in Section 4.2. A 10-point schemeConsider the following polynomial of degree 9 to determine the best curve fit todata/observations based on least squares techniquef (r ) f r 0 1r 2 r 2 3r 3 4 r 4 5r 5 6 r 6 7 r 7 8r 8 9r 9 ,(2)with respect to the observations ( xr r , f r ) for r n 1, , n, where n 5. We want to determinethe values of unknown parameters (betas) in (2) to make the following sum of squares of residuals R aminimum:R n [fr ( 0 1r 2 r 2 3r 3 4 r 4 5 r 5 6 r 6 7 r 7 8r 8 9 r 9 )]2 .r n 1Differentiating R with respect to 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 & 9 , and setting them to zerolead to a system of 10 normal linear equations. By solving it we get the following values ofunknowns. 315 1 0 0, 64 0 0 1,n(64n 560n 1036n 225)(16n4 520n2 3969)642
562G. Mustafa and M.T. Iqbal 0 1r ( n12r n 1rr) fr , 630n10 9240n8r 2 36036n6r 4 51480n 4r 6 24310n 2r 8 465n8r 60060n6r 3 270270n 4 r 5 437580n 2 r 7 230945r 9 21945n8 198660n6 r 2 270270n 4 r 4 368940n 2 r 6 546975r 8 127050n6r 1651650n 4 r 3 4954950n 2r 5 4011150r 7 2r 222684n6 515130n 4r 2 3939936n 2r 4 6756750r 6 1435665n 4r 12222210n 2r 3 18002985r 5 621885n 4 5304970n 2r 2 19594575r 4 5517600 n 2r 22336600r 3 264924n 2 13018500r 2 5314320r 907200, 165 1 1, 128 1 1 1 (4n4 5n2 1)(16n6 200n4 769n2 900) (16n8 920n6 19273n4 174105n2 571536)n, 1 3r ( n345r n 1rrr)f r, 2940n16 77616n14 r 2 360360n12 r 4 560560n10r 6 278460n8r 8 48510 n14r 840840n12r 3 3783780n10r 5 6126120n8r 7 3233230 n 6r 9 151410 n14 2910600n12r 2 8228220n10r 4 4204200n8r 6 2366910 n 6r 8 2870175n12r 42042000n10 r 3 504350n8r 5 193993800n6 r 7 72747675n 4r 9 2862825n12 30457812n10 r 2 4r 22612590n8r 4 213993780n 6r 6 154577787n 4r 8 66596145n10r 803632830n8r 3 2317985670n6r 5 2081349270n 4r 7 431636205n 2 r 9 22896335n10 73423350n8r 2 1874142270n6r 4 3292679390n 4r 6 1068248805n 2 r 8 776050275n8r 7407600200n6 r 3 15642551925n 4r 5 8647674750n 2 r 7 607385350r 9 43491105n8 3149091792n6 r 2 ,
AAM: Intern. J., Vol. 11, Issue 2 (December 2016) 5r 16458034593n 4 r 4 15182056890 n 2r 6 1547525538r 8 4829843865n6r 34223178990n 4 r 3 46679097465n 2r 5 10549324500 r 7 414265425n 6 19425143430n 4r 2 52986118185n 2r 4 19074034980 r 6 15762204150n 4r 73891517700n 2 r 3 47347850550r 5 2420539870 n 4 45106289976 n 2r 2 55081188162r 4 24443752080 n 2 r 58745258000 r 3 4368901320n 2 36215249400r 2 13976661600r 2385936000, 495 1 2 2, 32 2 2 (4n4 5n2 1)(16n6 200n4 769n2 900) (16n8 920n6 19273n4 174105n2 571536)n 2 6r ( n678r n 1rrr) fr , 2940n16 77616n14 r 2 360360n12 r 4 560560n10 r 6 278460n8r 8 48510 n14 r 840840n12 r 3 3783780n10 r 5 6126120n8r 7 3233230n6 r 9 151410 n14 2910600n12 r 2 8228220n10 r 4 4204200n8r 6 2366910n6 r 8 2870175n12 r 42042000n10 r 3 154504350n8r 5 193993800n6r 7 72747675n 4r 9 2862825n12 30457812n10r 2 22612590n8r 4 , 7r 213993780n6 r 6 154577787n 4 r 8 66596145n10 r 803632830n8r 3 2317985670n6r 5 2081349270n 4r 7 431636205n 2 r 9 22896335n10 73423350n8r 2 1874142270n 6r 4 3292679390n 4r 6 1068248805n 2r 8 776050275n8r 7407600200n6r 3 15642551925n 4 r 5 8647674750n 2 r 7 607385350r 9 43491105n8 3149091792n6r 2 16458034593n 4r 4 , 8r 15182056890n 2 r 6 1547525538r 8 4829843865n6r 34223178990n 4r 3 46679097465n 2 r 5 10549324500 r 7 414265425n6 19425143430n 4r 2 52986118185n 2 r 4 19074034980 r 6 15762204150 n 4 r 73891517700n 2r 3 47347850550r 5 2420539870n 4 45106289976n 2 r 2 55081188162 r 4 24443752080n 2 r 58745258000 r 3 4368901320 n 2 36215249400r 2 13976661600r 2385936000,563
564G. Mustafa and M.T. Iqbal 715 1 3, 32 3 3 3 (6n8 120n6 273n4 205n2 36)(4n2 25) n(n2 9)(4n4 113n2 784)(4n2 81), 3 9r ( n9r n 1r ) fr ,1011rr 58212n14r 720720n12r 3 2522520n10r 5 3341520n8r 7 1492260n 6r 9 13230n14 582120n12r 2 3783780n10r 4 7567560n8r 6 4594590n 6r 8 3395700n12r 37477440n10r 3 113513400n8r 5 124750080n6r 7 43275540 n 4r 9 760725n12 29106000n10r 2 160810650n8r 4 264864600n6r 6 126351225n 4r 8 77295834n10 , 10r 736756020n8r 3 1837655820n6r 5 1532810916n 4 r 7 335012370n 2r 9 17218845n10 556361190n8r 2 2495402910n6 r 4 3100807710n 4 r 6 934999065n 2 r 8 884164050n8r 6990743760n 6r 3 13405031640n 4r 5 7360016040n 2 r 7 637372670r 9 195862275n8 5128338600n6 r 2 17483541075n 4 r 4 14364400050n 2r 6 1708749900r 8 5426810466n 6r , 11r 33445936524n 4 r 3 43647433830 n 2 r 5 11145605484 r 7 1188565245n6 23692970070n 4 r 2 54603053505n 2 r 4 21108087000 r 6 17644803330n 4 r 75975179280n 2 r 3 50588087550 r 5 3760495200 n 4 51155666100n 2 r 2 61213452300r 4 27660129288n 2 r 64101510616 r 3 5585413680 n 2 40669794000r 2 16035117120 r 2834092800, 45045 1 4 4, 64 4 4 (256n14 8960n12 119392n10 766480n8 2475473n6 3822910n4 2400129n2 396900)n(4n4 145n 2 1296),1213 15015 1 n ( r r ) fr , 64 5 r n 1 5
AAM: Intern. J., Vol. 11, Issue 2 (December 2016) 12r565 17820n12 r 240240n10r 3 884520n8r 5 1211760n 6r 7 554268n 4r 9 5670n12 249480n10r 2 1621620n8r 4 3243240n 6r 6 1969110n 4r 8 926640n10 r 10810800n8r 3 33022080n 6r 5 35141040n 4r 7 11085360n 2r 9 274050n10 10187100n8r 2 54054000n 6r 4 83783700n 4r 6 36100350n 2r 8 18102150n8r 175014840n6r 3 414662976n 4r 5 300920400 n 2r 7 43325282r 9 , 13r 5044095n8 152834220n6r 2 624503880n 4r 4 661981320 n 2r 6 131164605r 8 169196280n6 r 1276669680n 4 r 3 2099719440 n 2r 5 777029880 r 7 44358300n 6 1031377050n 4 r 2 2913510600n 2 r 4 1620268650r 6 786456066 n 4r 4156898460n 2 r 3 3647492394r 5 191612925n 4 3077742690 n 2 r 2 4698779085r 4 1685913900n 2r 4817913100r 3 369576900n 2 3121836300 r 2 1230864624 r 217546560, 5 (64n12 1456n10 12012n8 44473n6 74074n4 48321n2 8100)(4n4 113n2 784)(4n2 81)n,1415 45045 1 n ( r r ) fr , 32 6 r n 1 6 14r 180n12 6160n10r 2 32760n8r 4 55440n6 r 6 29172n 4 r 8 6930n10 r 120120n8r 3 540540n6r 5 875160n 4r 7 461890n 2r 9 4110n10 46200n8r 2 278460 n 6r 4 1395240n 4 r 6 1239810n 2r 8 306075n8r 4204200n 6r 3 13963950 n 4r 5 14586000n 2 r 7 3464175r 9 13185n8 2351580n 6r 2 17645082n 4r 4 29655780n 2 r 6 , 15r 10567557 r 8 4777080n6r 49219170n 4r 3 110330220 n 2r 5 60167250 r 7 913320n6 36183290n 4 r 2 149292780n 2 r 4 124552890 r 6 32570175n 4 r 228006350n 2 r 3 270044775r 5 7403745n 4 166835790 n 2 r 2 338940693r 4 93392640n 2 r 335049000r 3 20115540n 2 209604780 r 2 79714800 r 13608000, 6 (16n6 56n4 49n2 9)(4n4 41n2 100) (16n8 920n6 19273n4 174105n2 571536)n,
566G. Mustafa and M.T. Iqbal1617 36465 1 n ( r r ) fr , 32 7 r n 1 7 16r 4620n10r 65520n8r 3 249480n6r 5 350064n 4r 7 163020n 2r 9 1890n10 83160n8r 2 540540n6 r 4 1081080n 4 r 6 656370n 2 r 8 207900n8r 2446080n6r 3 7234920n 4 r 5 7001280n 2 r 7 1684540r 9 74025n8 2633400 n6r 2 13063050n 4r 4 18018000n 2r 6 6016725r 8 3289440n6r 17r 30055116n 4 r 3 61954200n 2 r 5 32176716 r 7 1035720 n6 28253610 n 4r 2 97837740n 2r 4 74324250r 6 22649220 n 4 r 144314040 n 2r 3 159976740r 5 6279525n 4 117389250n 2r 2 215540325r 4 65491140 n 2r 218541284r 3 15295140n 2 143203500r 2 56461680r 9979200, 7 (256n16 13056n14 262752n12 2676752n10 14739153n8 43430478n6 63566689n4 38798964n2 6350400)(4n2 81)n,1819 109395 1 n ( r r ) fr , 64 8 r n 1 8 18r n10 2520n8r 2 13860n 6r 4 24024n 4r 6 12870n 2r 8 3465n8r 60060n 6r 3 270270n 4r 5 437580n 2r 7 230945r 9 525n8 21420n6r 2 348810n 4r 4 1021020n 2r 6 778635r 8 127050n6 r 1651650n 4r 3 4954950n 2r 5 , 19r 4011150r 7 28140n6 1398894n 4r 2 7549080n 2r 4 8702694r 6 1435665n 4r 12222210n 2r 3 18002985r 5 372575n 4 9667410 n 2r 2 22962555r 4 5517600n 2r 22336600r 3 1251180n 2 14004756r 2 5314320 r 907200, 8 (1024n18 72960n16 2108544n14 31989920n12 275773524n10 1367593305n8 3772135474n6 5304097665n4 3168117684n2 514382400) n,
AAM: Intern. J., Vol. 11, Issue 2 (December 2016)567 230945 1 n86 34 52 79 ( 630 n r 9240n r 36036n r 51480n r 24310r64 9 r n 1 9 315n8 13860n6 r 2 90090n 4 r 4 180180n 2 r 6 109395r 8 23520n 6 r 267960 n 4 r 3 720720n 2 r 5 531960r 7 9450n6 311850n 4 r 2 1351350n 2 r 4 1351350r 6 269934n 4 r 2074380n 2 r 3 2816814r 5 85995n 4 1850310 n 2 r 2 3918915r 4 1051860n 2 r 3946580r 3 258300n 2 2603700 r 2 1026576 r 181440) f r , 9 (4n4 113n2 784)(n2 1)(n2 9) (64n8 816n6 3276n4 4369n 2 900)(4n 2 81)n.By substituting all ’s in (2) and taking n 5, r 1/ 4 and r 3 / 4 , we get1358515988523094596996914549535f 4 f 3 f 2 f 1 83518895513856712155 f1 f2 f3 f4 f5 ,16777216838860883886083355443233554432f (1/ 4) f (3 / 4) 121551385671889556928354849845f 4 f 3 f 2 f 1 996923094515988513585 f1 f2 f3 f4 f5 .16777216838860883886083355443233554432If k represents subdivision level and i , then from the above rules we get the following 10point approximating scheme. 1 f 2ki 1 13585 fi k 4 159885 fi k3 923780 fi k 2 3879876 fi k1 29099070 fi k 9699690 fi k1 2771340 fi k 2 755820 fi k3 138567 fi k 4 12155 fi k5 , 1 f 2ki 11 12155 fi k 4 138567 fi k3 755820 fi k 2 2771340 fi k1 9699690 fi k 29099070 f 3879876 fki 1ki 2 923780 fki 3 159885 fki 4 13585 fki 5 ,where 33554432, fi k 1 and f i k are control points at refine and coarse level of iterations,respectively.Remark 1:(3)
568G. Mustafa and M.T. IqbalWe get different complexity schemes at different values of n . For example, at n 6 and 7, weget 12- and 14-point approximating schemes, respectively. By taking n 5 and evaluating (2) atr 1/ 6, r 3 / 6 and r 5 / 6 , we get 10-point ternary approximating scheme. Similarly, we geteven-point quaternary, quinary and higher arity approximating schemes.3. Analysis of the schemeIn this section, we present the analysis of 10-point scheme by using the methodology presentedin Hormann (2012). Analysis includes continuity, reproduction, generation and limit analysis ofthe scheme.3.1.ContinuitySince the sum of coefficients in the refinement rule of f 2ki 1 and the sum of coefficients in therefinement rule of f 2ki 11 are both equal to one, the necessary condition for the convergence of thescheme is satisfied. The Laurent polynomial of the scheme is1 [13585 z 0 12155 z1 159885 z 2 138567 z 3 923780 z 410 33554432z 5 755820 z 3879876 z 6 2771340 z 7 29099070 z 8 9699690 z 9 9699690 z10 ( z) (4) 29099070 z11 2771340 z12 3879876 z13 755820 z14 923780 z15 138567 z16 159885 z17 12155 z18 13585 z19 ].It can be written as 1 z b( z ), 2 ( z) where1 b( z ) [12155 z 0 1430 z1 139997 z 2 19888 z 3 775708 z 4 148072 z 510 16777216z 6 2919412 z 960464 z 7 10660154 z 8 18438916 z 9 10660154 z10 960464 z11 2919412 z12 148072 z13 775708 z14 19888 z15 139997 z16 1430 z17 12155 z18 ].Let S c be the difference scheme corresponding to c( z ) obtained from b( z ), where
AAM: Intern. J., Vol. 11, Issue 2 (December 2016)5691 c( z ) [12155 z 0 10725 z1 129272 z 2 109384 z 3 666324 z 410 16777216 z 518252 z 5 2401160 z 6 1440696 z 7 9219458 z 8 9219458 z 9 1440696 z10 1440696 z11 2401160 z12 518252 z13 666324 z14 109384 z15 129272 z16 10725 z17 12155 z18 ],then ‖ Sc ‖ max[ sum of modulus of odd coefficients in c z , sum of modulus of evencoefficients in c( z ) ] 14507426/16777216 0.8647 1. So S c is contractive and the schemeSb corresponding to b( z ) is convergent. So, scheme S i.e. scheme (3) is C 1 - continuous.Now we write ( z ) as follows 1 z ( z) b1 ( z ), 2 where21 b1 ( z ) [12155 z 0 10725 z1 129272 z 2 109384 z 3 666324 z 410 8388608z 5 518252 z 2401160 z 6 1440696 z 7 9219458 z 8 9219458 z 9 1440696 z10 2401160 z11 518252 z12 666324 z13 109384 z14 129272 z15 10725 z16 12155 z17 ].Again let Sc1 be the difference scheme corresponding to c1 ( z ) obtained from b1 ( z ) , where1 c1 ( z ) [12155 z 0 35035 z1 71357 z 2 287133z 3 163415z 410 8388608 z 1132215 z 5 300145z 6 3173201z 7 3173201z 8 300145z 9 1132215z10 163415 z11 287133z12 71357 z13 35035z14 12155z15 ],then ‖ Sc1 ‖ 0.6168 1. SoC 2 continuous.Again ( z ) can be written as 1 z b2 ( z ), (5) 2 3 ( z) schemeSc1 is contractive and Sb1 is convergent. So, S is
570G. Mustafa and M.T. Iqbal1 b2 ( z ) [12155 z 0 22880 z1 106392 z 2 215776 z 3 450548z 410 4194304 z 968800 z 5 1432360 z 6 2873056 z 7 634602 z 8 2873056z 9 1432360z10 968800 z11 450548z12 215776 z13 106392 z14 22880z15 12155z16 ].Let Sc2 be the difference scheme corresponding to c2 ( z ) obtained from b2 ( z ) , where1 c2 ( z ) [12155 z 0 47190 z1 24167 z 2 311300 z 3 147885z 410 4194304z 5 984330 z 684185z 6 2489016 z 7 684185z 8 984330z 9 147885z10 311300 z11 24167 z12 47190 z13 12155z14 ],then ‖ Sc2 ‖ 1.233 1.So Sc2 is not contractive and Sb2 is not convergent. So,S is not C 3 continuous. Thus,proposed 10-point scheme is C 2 -continuous.3.2. Polynomial generation and reproductionIn this section, we will discuss the degree of the polynomial generation and polynomialreproduction of the proposed scheme.Since by (5) 1 z ( z) 2 2 1b2 ( z ) ,then the degree of polynomial generation is 2.Now by taking derivative of ( z ) with respect to z and then by substituting z 1 , we get (1)1 (1) 1 . This implies that . This further implies that22i 1i 1/2tik k .222kThus, by Hormann (2012) the proposed scheme has dual parameterization. Sincek 1 1l 0 k (1) 2 l and k ( 1) 0 ,2
AAM: Intern. J., Vol. 11, Issue 2 (December 2016)571for k 0,1, 2, where k ( z ) is the k derivative of ( z ) then, again by Hormann (2012), a 10-pointbinary subdivision scheme reproduces polynomials of degree 2 with respect to theparameterizationtik 1 i 1/ 2 .22k3.3. Local AnalysisIn this section, by using local analysis, we can find the limit position of control point of theinitial control polygon on the limit curve with the help of limit stencil. For this, we consider thefollowing matrix representation of scheme (3) for i 4, 3, 2, 1,0,1, 2,3, 4 ,F k 1 SF k ,F k 1 [ f k8 1 , f k7 1 , f k6 1 , f k5 1 , f k4 1 , f k3 1 , f k2 1 , f k1 1 , f 0k 1 , f1k 1 , f 2k 1 , f 3k 1 , f 4k 1 ,f5k 1 , f 6k 1 , f 7k 1 , f8k 1 , f9k 1 ]T ,F k [ f k8 , f k7 , f k6 , f k5 , f k4 , f k3 , f k2 , f k1 , f0k , f1k , f 2k , f3k , f 4k , f5k , f6k , f7k , f8k , f9k ]T , t 0 0 0 0 0 01 0S 0 0 0 0 0 0 0 0 lsr lt s00 0 0 0 0 0 0 0 q p o n m l 0 0 0 00 0 0 0 m n o p q r s t0 0 0 0 0 0 0 r q p o n m l 0 0 0 00 0 0 l m n o p q r s t0 0 0 0 0 0 s r q p o n m l 0 0 0 00 0 l m n o p q r s t 0 0 0 0 0 t s r q p o n m l 0 0 0 00 0 l m n o p q r s t0 0 0 0 , 0 t s r q p o n m l 0 0 0 0 0 0 l m n o p q r s t0 0 0 0 0 t s r q p o n m l 0 0 0 0 0 0 l m n o p q r s t0 0 0 0 0 t s r q p o n m l 0 0 0 0 0 0 l m n o p q r s t0 0 0 0 0 t s r q p o n m l 0 0 0 0 0 0 l m n o p q r st m 0 t0 00 00 00 00 00 00 00 00 00 00 0n opqrstwhere 33554432, 13585 , l 159885, m 923780 , n 3879876 , o 29099070,p 9699690, q 2771340, r 755820, s 138567 and t 12155.The invariant neighborhood size of the matrix S is 18 and its eigenvalues are:
572G. Mustafa and M.T. Iqbal 1.000, 0.5000, 0.2500, 0.1250, 0.0625, 0.0287, 0.0346, 0.0312, 0.0198,0.0156, 0.0104, 0.0089, 0.0078, 0.0026, 0.0025, 0.0039, 0.0020, 0.0010.If 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11, 12 , 13 , 14 , 15 , 16 , 17 and 18 are the eigenvectorscorresponding to these eigenvalues, then Q is the matrix whose columns are these eigenvectors.If D is a diagonal matrix whose diagonal entries are the above eigenvalues, then by theeigenvalue decomposition S QDQ 1. By performing simple algebraic operation we getS k QDk Q 1. Since the largest eigenvalue is one and other values are less than one so lim D is akk matrix whose first left top entry is one and other entries are zeros. Sincef k 1 Sf k S (Sf k 1 ) S 2 f k 2 . S k f 0 then f k 1 (QDk Q 1 ) f 0 . Taking limit, we getf Q(lim Dk )Q 1 f 0 . This implies thatk f 8f 7f 6f 5f 4f 3f 2f 1f 0 f1 f 2 f 3 f 4 f 5 f 6 f 7 f 8 f 9 iˆ iˆ iˆ ˆ i iˆ iˆ iˆ iˆ ˆ i iˆ iˆ iˆ iˆ ˆ i ˆ i iˆ iˆ iˆ ˆˆ nˆ oˆ pˆ qˆ rˆ sˆ tˆ uˆ vˆ wˆ xˆ yˆ zˆ j kˆ lˆ m ˆˆ nˆ oˆ pˆ qˆ rˆ sˆ tˆ uˆ vˆ wˆ xˆ yˆ zˆ j kˆ lˆ m ˆˆ nˆ oˆ pˆ qˆ rˆ sˆ tˆ uˆ vˆ wˆ xˆ yˆ zˆ j kˆ lˆ m ˆˆ nˆ oˆ pˆ qˆ rˆ sˆ tˆ uˆ vˆ wˆ xˆ yˆ zˆ j kˆ lˆ m ˆˆ nˆ oˆ pˆ qˆ rˆ sˆ tˆ uˆ vˆ wˆ xˆ yˆ zˆ j kˆ lˆ m ˆˆ nˆ oˆ pˆ qˆ rˆ sˆ tˆ uˆ vˆ wˆ xˆ yˆ zˆ j kˆ lˆ m ˆˆ nˆ oˆ pˆ qˆ rˆ sˆ tˆ uˆ vˆ wˆ xˆ yˆ zˆ j kˆ lˆ m ˆˆ nˆ oˆ pˆ qˆ rˆ sˆ tˆ uˆ vˆ wˆ xˆ yˆ zˆ j kˆ lˆ m ˆˆ nˆ oˆ pˆ qˆ rˆ sˆ tˆ uˆ vˆ wˆ xˆ yˆ zˆ j kˆ lˆ mˆˆ nˆ oˆ pˆ qˆ rˆ sˆ tˆ uˆ vˆ wˆ xˆ yˆ zˆ j kˆ lˆ m ˆˆ nˆ oˆ pˆ qˆ rˆ sˆ tˆ uˆ vˆ wˆ xˆ yˆ zˆ j kˆ lˆ m ˆˆ nˆ oˆ pˆ qˆ rˆ sˆ tˆ uˆ vˆ wˆ xˆ yˆ zˆ j kˆ lˆ m ˆˆ nˆ oˆ pˆ qˆ rˆ sˆ tˆ uˆ vˆ wˆ xˆ yˆ zˆ j kˆ lˆ m ˆˆ nˆ oˆ pˆ qˆ rˆ sˆ tˆ uˆ vˆ wˆ xˆ yˆ zˆ j kˆ lˆ m ˆˆ nˆ oˆ pˆ qˆ rˆ sˆ tˆ uˆ vˆ wˆ xˆ yˆ zˆ j kˆ lˆ m ˆˆ nˆ oˆ pˆ qˆ rˆ sˆ tˆ uˆ vˆ wˆ xˆ yˆ zˆ j kˆ lˆ m ˆˆ nˆ oˆ pˆ qˆ rˆ sˆ tˆ uˆ vˆ wˆ xˆ yˆ zˆ j kˆ lˆ m ˆˆ nˆ oˆ pˆ qˆ rˆ sˆ tˆ uˆ vˆ wˆ xˆ yˆ zˆ j kˆ lˆ m Hence, the limit stencil is iˆ whereˆj kˆ lˆ mˆ nˆ oˆpˆ qˆ rˆ sˆ tˆ uˆ vˆ wˆ xˆyˆ zˆ , f 08 f 07 f 06 f 05 f 04 f 03 f 02 f 01 f 00 .f10 f 20 f 30 f 40 f 50 f 60 f 70 f 80 f 90
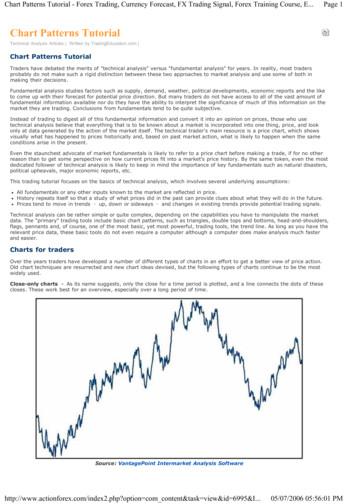
AAM: Intern. J., Vol. 11, Issue 2 (December 2016)573iˆ 0.0000, ˆj 0.0000, kˆ 0.0000, lˆ 0.0000, mˆ 0.0007, nˆ 0.0070,oˆ 0.0365, pˆ 0.1370, qˆ 0.6068, rˆ 0.6068, sˆ 0.1370, tˆ 0.0365,uˆ 0.0070, vˆ 0.0007, wˆ 0.0000, xˆ 0.0000, yˆ 0.0000, zˆ 0.0000.This means that when we apply this stencil to the initial pointsf 08 , f 07 , f 06 , f 05 , f 04 , f 03 , f 02 , f 01 , f00 , f10 , f 20 , f30 , f 40 , f50 , f 60 , f 70 , f80 , f90we get the limit position of the central one i.e., f 00 .4. Applications and conclusionHere are the numerical examples (see Figures 1-2), which show that the proposed scheme issuitable for fitting data. Different types of data have been fitted by 10-point approximatingschemes.Figure 1. Limit curve is fitted by 10-point scheme whereas solid diamonds show the initialcontrol points.Figure 2. Limit curve is fitted by 10-point scheme whereas solid diamonds show the initialcontrol points.
574G. Mustafa and M.T. Iqbal4.1. ConclusionIn this paper, a 10-point approximating scheme is presented by fitting 9-degree polynomial todata by least squares algorithm. Analysis of 10-point scheme is also presented. Analysis includescontinuity, polynomial generation and reproduction and local limiting analysis. It is shown thatproposed scheme is C 2 -continuous that is fitting curve to data is smooth enough. The polynomialgeneration and reproduction of the scheme is 2. Limiting mask/stencil is also presented to findpoint on the limiting curve. Results show that 10-point scheme has nearly interpolating behavior.The families of 2m and (2m 1) -point binary, ternary, ,b -ary approximating schemes byfitting different degree polynomials to data by least squares algorithm can be constructed byproposed framework.Acknowledgement:The authors would like to thank the referees for their helpful suggestions and comments whichshowed the way to improve this work. This work is supported by NRPU (P. No. 3183) HECPakistan.REFERENCESCostantini, P. and Manni, C. (2010). Curve and surface construction using Hermite subdivisionschemes. Journal of Computational and Applied Mathematics, Vol. 233, No. 7, pp. 16601673.Deslauriers, G., and Dubuc, S. (1989). Symmetric iterative interpolation processes. ConstructiveApproximation, Vol. 5, pp. 49-68.Dyn, N., Gregory, J. A. and Levin, D. (1991). Analysis of uniform binary subdivision schemesfor curve design. Constructive Approximation, pp. 127-147.Dyn, N., Head, A., Hormann, K. and Sharon, N. (2015). Univariate subdivision schemes fornoisy data with geometric applications. Computer Aided Geometric Design, Vol. 37, pp. 85104.Hormann, K. (2012). Subdivision scheme for geometric modelling: a hands-on tutorial.Dolomites Research Notes on Approximation, Vol. 5, ISSN 2035-6803, Publisher:University of Verona.Lian, J-A. (2009). On a-ary subdivision for curve design: I. 2m point and 2m 1 pointinterpolatory schemes. Applications and Applied Mathematics: An International Journal,Vol. 4, No. 1, pp. 434-444.Mustafa, G., Ashraf, P. and Deng, J. (2014). Generalized and unified families of interpolatingsubdivision schemes. Numerical Mathematics: Theory Methods and Applications, Vol. 7,No. 2, pp. 193-213.Mustafa, G., Ashraf, P. and Saba N. (2016). A new class of binary approximating subdivisionschemes. JurnalTeknologi, Vol. 78, No. 4, pp. 65–72.
AAM: Intern. J., Vol. 11, Issue 2 (December 2016)575Mustafa, G., Hao, L., Zhang, J. and Deng, J. (2015). 𝑙1 -regression based subdivision schemes fornoisy data. Computer-Aided Design, Vol. 58, pp. 189-99.Mustafa, G. and Zahid, M. (2013). Numerical algorithm for analysis of 𝑛 ary subdivisionschemes. Applications and Applied Mathematics: An International Journal, Vol. 8, No. 2,pp. 614-630.Romani L. (2015). A Chaikin-based variant of Lane-Riesenfeld algorithm and its non-tensorproduct extension, Computer Aided Geometric Design Vol. 32, pp. 22-49.
least squares technique instead of other techniques. The method of least squares is one of the golden techniques in statistics for curve fitting. In this modern era method of least squares is frequently used to find numerical values of the parameters to fit a function to set of data. It means that the overall solution minimizes the sum of the .
Eden Pines Colony Subdivision #277 Big Pine. Tropical Bay Subdivision #459 Geiger. Boca Chica Ocean Shores Subdivision #29 Key Largo Sexton Cove Estates Subdivision #472 Geiger. Geiger Mobile Homes Subdivision #132 Plantation Key #147 Matecumbe K #282 Big Pine #458 Geiger # 28 Key Largo Culvert Installation #293 Big Pine Weed Barrier
subdivision plat index subdivision name tract volume file # beverly heights 5 21 bley-was heights 1094 20 26, 26b bley-was heights - first addition 1102 20 27, 27b bly - first addition 6 37 bly - north 5 17 bly - town of 5 16, 16b bonanza 1 6, 6b bonanza - bowne addition 1b 4a bonanza - davis subdivision 1224 22 21, 21b bonanza - east 1b 12b bonanza - first addition 1 28, 28b
Shirley, Fundamentals of Computer Graphics Loop Subdivision SIGGRAPH 2000 course notes Subdivision for Modeling and Animation (page 70) Catmull Clark Subdivision "Subdivision Surfaces in Character Animation", DeRose, Kass & Truong, SIGGRAPH 1998 Questions? Justin Legakis Toda
PART 5 SUBDIVISION & DEVELOPMENT 27 . Queenstown Lakes District Council -Proposed District Plan Decisions Version (Apr 2022) 27-1. 27 Subdivision and Development . 27.1 Purpose . Subdivision and the resultant development enables the creation of new housing and land use opportunities, and is a key driver of the District's economy.
Section 6.3 Approximating Square Roots 247 EXAMPLE 2 Approximating Square Roots Estimate — 52 to the nearest integer. Use a number line and the square roots of the perfect squares nearest to the radicand. The nearest perfect square less than 52 is 49. The nearest perfect square greater than 52 is 64. Graph 52 . 49 7 64 8
Mar 26, 2021 · ssr1428 richard roop entrance plans subdivision n/a 1996 ssr1448 quality mechanical, inc. entrance plans subdivision n/a 1998 ssr1457 niblett, norris l. entrance plans subdivision n/a 1997 ssr1681 dollar general, laurel entrance plans subdivision approved 2002 ssr1829 i
SUBDIVISION REGULATIONS City of Vestavia Hills, Alabama April 8, 2010 p. 1-2 §1.6. Penalties The City of Vestavia Hills shall initiate any appropriate action or procedure to prevent the unlawful subdivision of land and to prevent occupancy of such subdivision of land under the authority conferred by Section 13 Act No. 84-454, State of Alabama.
Subdivision & Infrastructure Design Manual 1-2 1.2.9 The word "herein" means "in this manual" and the word "regulations" means "the Pinal County Subdivision Regulations". 1.2.10 The word "person" includes a corporation, a partnership, and an unincorporated association of persons such as a club.