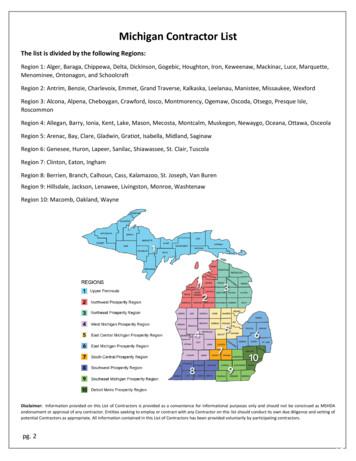
332: Mechanical Behavior Of Materials - Northwestern University

4STRESS AND STRAIN4.2Tensor Transformation Law312Figure 4.2: 3 dimensional stress tensorIn graphical form the relationship is as shown in Figure 4.2. Like the 2dimensional stress tensor mentioned above, the 3-dimensional stress tensormust also be symmetric in order for static equilibrium to be achieved. Thereare therefore 6 independent components of the three-dimensional stress tensor: 3 normal stresses, σ11 , σ22 and σ33 , describing stresses applied perpendicular to the 1, 2 and 3 faces of the cubic volume element. 3 shear stresses: σ12 , σ23 and σ13 .The three dimensional stress tensor is a 3x3 matrix with 9 elements (thoughonly 6 are independent), corresponding to the three stress components actingon each of the three orthogonal faces of cube in the Cartesian coordinate system used to define the stress components. The 1 face has n1 1, n2 0 andn3 0. By setting n (1, 0, 0) in Eq. 4.2, we get the following for the stressesacting on the 1 face of the volume element:P1 /A σ11P2 /A σ12P3 /A σ13(4.4)Equivalent expressions can be obtained for the stresses acting on the 2 and 3faces, by setting n (0, 1, 0) and n (0, 0, 1), respectively.4.2Tensor Transformation LawThe stress experienced by a material does not depend on the coordinate system used to define the stress state. The stress tensor will look very different ifwe chose a different set of coordinate axes to describe it, however, and it is important to understand how changing the coordinate system changes the stresstensor. We begin in this section by describing the procedure for obtaining the9

4.2Tensor Transformation Law422'2'2222'12'12'1212113STRESS AND STRAIN111'113' 3Figure 4.3: Rotation of coordinate system. The coordinate system is rotated byθabout the 3 axis, transforming the 1 axis to10 and the 2 axis to20 .stress tensor that emerges from a given change in the coordinate system. Wethen describe the method for obtaining a specific set of coordinate axis whichgives a diagonalized tensor where only normal stresses are present (Section4.3).4.2.1Specification of the Transformation MatrixIn general, we consider the case where our 3 axes (which we refer to simply asaxes 1, 2 and 3) are moved about the origin to define a new set of coordinateaxes that we refer to as 10 , 20 and 30 . As an example, consider the simple counterclockwise rotation around the 3 axis by an angle φ, shown schematically inFigure 4.3. In general, the relative orientation of the transformed (rotated) anduntransformed coordinate axes are given by a set of 9 angles between the 3untransformed axes and the three transformed axes. In our notation we specify these angles as θij , where i specifies the transformed axes (10 , 20 or 30 ) and jspecifies the untransformed axis (1, 2 or 3). In our simple example, the anglebetween the 1 and 10 axes is φ, so θ11 φ. The angle between the 2 and 20 axesis also φ, so θ22 φ. The 3 axis remains unchanged in our rotation example,so θ33 0. The 3/30 axis remains perpendicular to the 1,10 , 2,20 axes, so wehave θ31 θ32 θ13 θ23 90 . Finally, we see that the angle between the 10and the 2 axis is 90 φ (θ12 90 φ) and the angle between the 20 and 1 axisis 90 φ (θ21 90 φ). The full [θ ] matrix in this case is as follows: φ90 φ 90φ90 (4.5)[θ ] 90 φ90900Note that the [θ ] matrix is NOT symmetric (θij 6 θ ji ), so you always need tomake sure the first index, i, (denoting the row in the [θ ] matrix) corresponds tothe transformed axes, and the second index, j (denoting the column in the [θ ]matrix) corresponds to the original, untransformed axes.10

4STRESS AND STRAIN4.2.24.2Tensor Transformation LawExpressions for the Stress ComponentsOnce we specify all the different components of [θ ], we can use the following general expression to obtain the stresses in the new (primed) coordinatesystem as a function of the stresses in the original coordinate system:σij0 cos θ jk cos θil σkl(4.6)k,lFor each component of the stress tensor, we have to sum 9 individual terms0 is given as follows:(all combinations of k and l from 1 to 3). For example, σ120 cos θ cos θ σ cos θ cos θ σ cos θ cos θ σ σ122111 112112 122113 13cos θ22 cos θ11 σ21 cos θ22 cos θ12 σ22 cos θ22 cos θ13 σ23 cos θ23 cos θ11 σ31 cos θ23 cos θ12 σ32 cos θ23 cos θ13 σ33(4.7)The calculation is breathtakingly tedious if we do it all by hand, so it makessense to automate this and do the calculation via computer, in our case withPython. In this example we’ll start with a simple stress state corresponding touniaxial extension in the 1 direction, with the following untransformed stresstensor:5x106 [σ] 00 0 00 0 0 0(4.8)Suppose we want to obtain the stress tensor in the transformed coordinatesystem obtained from a 45 counterclockwise rotation around the z axis. Therotation matrix is given by Eq. 4.5, with φ 45 . The following Python codesolves for the full transformed tensor, with σij given by Eq. 4.8 and θij givenby Eq. 4.5 with φ 45 :12#!/ usr / bin / env python3# -* - coding : utf -8 -* -34import numpy as np567sig np . zeros ((3 , 3) ) # % create stress tensor and set to zerosig [0 , 0] 5 e6 ; # this is the only nonzero component89sigp np . zeros ((3 , 3) ) # initalize rotated streses to zero1011phi 451213theta [[ phi ,90 - phi ,90] , [90 phi , phi ,90] , [90 ,90 ,0]]11

4.2Tensor Transformation Law4STRESS AND STRAINFigure 4.4: Output generated by rotate45.py.141516171819theta np . deg2rad ( theta ) # trig functions need angles inradiansfor i in [0 , 1 , 2]:for j in [0 , 1 , 2]:for k in [0 , 1 , 2]:for l in [0 , 1 , 2]:sigp [i , j ] sigp [i , j ] np . cos ( theta [i , k ]) * np . cos (theta [j , l ]) * sig [k , l ]2021print ( sigp )# display the transformed tensor componentsWe use Python because it is free, powerful, and quite easy to learn especiallyif you have experience with a similarly-structured programming environmentlike MATLAB. Various Python code examples are included in this text, and arepresented as examples of how to do some useful things in Python.The output generated by the Python code is shown in Figure 4.4, and corresponds to the following result: 2.5x106 0 σ 2.5x1060 2.5x1062.5x1060 00 0(4.9)Note the following: The normal stresses in the 1 and 2 directions are equal to one another. The transformed shear stress in the 1-2 plane is half the original tensilestress. The sum of the normal stresses (the sum of the diagonal components ofthe stress tensor) is unchanged by the coordinate transformation4.2.3An Easier Way: Transformation by Direct Matrix MultiplicationA much easier way to do the transformation is to use a little bit of matrix math.The approach we use is described in a very nice web page put together by Bob12

4STRESS AND STRAIN4.2Tensor Transformation LawMcGinty[3]: A transformation matrix, Qij , is obtained by taking the cosinesof all of these angles describing the relationship between the transformed anduntransformed coordinate axes:[Q] cos [θ ](4.10)For the simple case of rotation about the z axis, the angles are given by Eq. 4.5,so that [Q] is given as: cos φ[Q] cos (90 φ)cos 90cos (90 φ)cos φcos 90 cos 90cos φcos 90 sin φcos 00sin φcos φ0 00 1(4.11)The transformed stress is now obtained by the following simple matrix multiplication: 0 σ [Q] [ σ ] [Q] T(4.12)where the[Q] T is the transpose of[Q]:Q T (i, j) Q( j, i )(4.13)For the rotation by φ around the z axis, [Q] T is given by the following: cos φ[Q] T sin φ0 sin φ 0cos φ 0 01(4.14)Equation 4.12 is much easier to deal with than Eq. 4.7. The Python code to takea uniaxial stress state and rotate the coordinate system by 45 about the 3 axislooks like this if we base it on Eq. 4.12:1import numpy as np234# create stress tensor with all zero elementssig np . zeros ((3 ,3) )567# set first one elment to be nonzero ( one of the normal stresses )sig [0][0] 5 e68910# set the rotation anglephi 45111213# define the rotation matrix in degreestheta np . array ([[ phi ,90 phi ,90] ,[90 - phi , phi ,90] ,[90 ,90 ,0]])13

4.3Principal Stresses4STRESS AND STRAINFigure 4.5: Principal Stresses141516# now put all the direction cosines in QQ np . cos ( np . radians ( theta ) )171819# claculate the transpose of QQT np . transpose ( Q )20212223# now multiply everything together# note that we use the @ sign to multiply matrices in pythonsigp np . round ( Q@sig@QT )242526# print the resultprint ( sigp )Running this script gives the output shown in Figure 4.4, i.e. we obtain exactlythe same result we obtained by using Eq. 4.7.4.3Principal StressesAny stress state (true stress) can be written in terms of three principal stressespppσ1 , σ2 and σ3 , applied in three perpendicular directions as illustrated in Figure 4.5. Note that we still need 6 independent parameters to specify a stressstate: the 3 principal stresses, in addition to three parameters that specify theorientation of the principal axes. The stress tensor depends on our definitionof the axes, but it is always possible to chose the axes so that all of the shearcomponents of the stress tensor vanish, so that the stress tensor looks like thefollowing: pσ1[σ] 000pσ20 00 pσ3(4.15)In order to gain some insight into the points mentioned above, it is usefulto consider a range of rotation angles, and not just a singe rotation angle of45 . One way to do this is to use the symbolic math capability of Python (or14

4STRESS AND STRAIN4.3Principal Stressesyour other favorite software) to obtain the full stress tensor as a function of therotation angle. We’ll use the principal axes to define our untransformed state,and transform to a new set of axes by rotating counterclockwise by an angle φaround the 3 axis. We want to calculate[σ0 ] from Eqs.4.11 and 4.12 as we did before, but we leave φ as an independentvariable. We use the following python script to do this:123# mohr circle . py# Mohr 's circle derivationfrom sympy import symbols , Matrix , cos , pi , simplify , preview4567# specify the principal stressesSsig1p , sig2p , sig3p symbols ([ ' sigma 1 p ' , ' sigma 2 p ' , ' sigma 3 p ' ])sig Matrix ([[ sig1p , 0 , 0] , [0 , sig2p , 0] , [0 , 0 , sig3p ]])8910# now specify the rotation anglephi symbols ( ' phi ')111213# specify the theta matrixtheta Matrix ([[ phi , pi /2 - phi , pi /2] , [ pi /2 phi , phi , pi /2] ,[ pi /2 , pi/2 ,0]])141516# take the cosine of all the elements in the matrix to get QQ theta . applyfunc ( cos )171819# get the transpose of the matrixQT Q . transpose ()202122# now do the matrix m ultipl icatio n to get the transformed matrixsigp Q * sig * QT23242526# now simplify and show the outputexp1 simplify ( sigp )preview ( exp1 , filename ' ./ figures / sy mpy m o hr e x p1 . svg ')272829# define the center ( C ) and radius ( R ) of the circleR , C symbols ([ 'R ' , 'C ' ])30313233# now we rewrite in terms of center and radius and simplify againsigp sigp . subs ([( sig1p , C R ) , ( sig2p , C - R ) ])exp2 simplify ( sigp )34353637# now save the exp1 and exp2 as image filespreview ( exp1 , viewer ' file ' , filename ' ./ figures /s ym py mo hr ex p1 . png ')preview ( exp2 , viewer ' file ' , filename ' ./ figures /s ym py mo hr ex p2 . png ')This results in the following expression for [σ0 ] (exp1, generated in line 26 ofmohr circle.py).15

4.3Principal Stresses4STRESS AND STRAINThis is not yet a very illuminating result, but it is the basis for the Mohr circleconstruction, which provides a very useful way to visualize two dimensionalstress states. This construction is described in more detail in the followingSection.4.3.1Mohr’s Circle ConstructionThe Mohr circle is a graphical construction that can be used to describe atwo dimensional stress state. A two dimensional stress state is specified bypptwo principal stresses, σ1 and σ2 , and by the orientation of the principalppaxes. The Mohr circle is drawn with a radius, R, of σ1 σ2 , centered atC ppσ1 σ2 /2 on the horizontal axis. We can use these values of R andC as the independent variables in the expression for σ0 that we obtained fromour python script. This substitution is made in lines 30-34 of mohr circle.py,and leads to the following expression for [σ0 ] (exp2 from line 34):Python has taken us almost as far as we need to go, but it doesn’t seem to besmart enough to use the following two trigonometric identities:1 2 sin2 φ cos (2φ)1 2 cos2 φ cos (2φ)(4.16)Substituting these into the expression for [σ0 ] gives our final result: C R cos (2φ) 0 σ R sin (2φ)0 R sin (2φ)0C R cos (2φ) 0 p0φ3(4.17)In the Mohr circle construction normal stresses (σN ) are plotted on the x axisand the shear component of the stress tensor (τ) is plotted on the y axis. Fora two dimensional stress state in the 1-2 plane the circle is defined by twopoints: (σ11 , σ12 ) and (σ22, σ12 ). In our current example the stress state in16

4STRESS AND STRAIN4.3Principal StressesFigure 4.6: Mohr’s circle construction.the untransformedaxesrepresentedby the open symbols in Figure 4.6, i.e. is ppby the points σ1 , 0 and σ1 , 0 . In the transformed axes the stress state isrepresented by the solid circles in Figure 4.6. From Eq. 4.17 it is evident thatthe relationship between the two different representations of the stress state isobtained by a rotation along circle by 2φ. Whether this rotation is clockwiseor counterclockwise depends on the sign convention in the definition of theshear stress. We’re not going to worry about it here, but you can refer to theMohr’s Circle Wikipedia article[4] for the details (see the Section on the signconvention).The Mohr circle construction can only be applied for a two dimensional meaning that there are no shear stresses with a component in the direction of therotation axis. There can be a normal stress in the third direction, as in our example above, because this normal stress is simply superposed on the 2d stresspppstate. In general, there are three principal stresses, σ1 , σ2 and σ3 , and we candraw the Mohr circle construction with any combination of these 3 stresses. Weend up with 3 different circles, as shown in Figure 4.7. Note that the convenpption is that σ1 is the largest principal stress and that σ3 is the smallest principalpppstress, i.e. σ1 σ2 σ3 . An important result is that the largest shear stress,τmax , is given by the difference between the largest principal stress and thesmallest one:τmax 1 ppσ1 σ32(4.18)This maximum shear stress is an important quantity, because it determineswhen a material will deform plastically (much more on this later). In order17

4.3Principal Stresses4STRESS AND STRAINFigure 4.7: Three-dimensional Mohr’s Circle.to determine this maximum shear stress, we need to first Figure out what theprincipal stresses are. In some cases this is easy. In a uniaxial tensile test, one ofthe principals stresses is the applied stress, and the other two principal stressesare equal to zero.The individual Mohr’s circles in Figure 4.7 correspond to rotations in thearound the individual principal axes. Circle C1 corresponds to rotation aroundpthe direction in which σ1 is directed, C2 corresponds to rotation around thepdirection in which σ2 is directed, and C3 corresponds to rotation around thepdirection in which σ3 is directed. A consequence of this is that is always possible to use the Mohr’s circle construction to determine the principal stresses ifthere is only one non-zero shear stress.1) Exercise:state:Determine the maximum shear stress for the following stress 3[σ] 02030 20 MPa5(4.19)2) Solution:We can handle this one without using a computer. Thereis only one non-zero shear stress (σ13 ), so we can determine the principals18

4STRESS AND STRAIN4.3Principal Stressesstresses in the following manner:1. One of the three principal stresses is the normal stress in the directionthat does not involve either of the directions in the nonzero shear stress.Since the non-zero shear stress in our example is σ13 , one of the principal stresses is σ22 3 MPa.2. Now we draw a Mohr circle construction using the two normal stressesand the non-zero shear stress, in this case σ11 , σ33 and σ13 . Mohr’s circleis centered at the the average of these two normal stresses, in our caseat C (σ11 σ33 ) /2 4 MPa.3. Determine the radius of the circle, R, is given as:R q2 (σ33 σc )2 σ13q2 2.24 MPa(5 4)2 σ134. The principal stresses are given by the intersections of the circle withthe horizontal axis:σ p C R 6.24 MPa, 1.76 MPaThe third principal stress is 3 MPa, as we already determined.5. The maximum shear stress is half the difference between the largestprincipal stress (6.64 MPa) and the smallest one (1.76), or 2.24 MPa.4.3.2Critical Resolved Shear Stress for Uniaxial TensionAs an example of the Mohr circle construction we can consider the calculation of the resolved shear stress on a sample in a state of uniaxial tension. TheMohr’s circle representation of the stress state is shown in Figure 4.8. The resolved shear stress, τrss , for sample in uniaxial tension is given by the followingexpression:19

4.3Principal Stresses4STRESS AND STRAINpτrss σ1 cos φ cos λ(4.20)pwhere σ1 is the applied tensile stress, φ is the angle between the tensile axisand a vector normal to the plane of interest, and λ is the angle between thetensile axis and the direction of the shear stress. This shear stress has to be inthe plane itself, so for a 2-dimensional sample λ φ 90 . This means we canrewrite Eq. 4.20 in the following way:pτrss σ1 cos φ cos (90 φ)(4.21)We can use the identities cos (90 φ) sin φ and sin (2φ) 2 sin φ cos φ toobtain the following:pτrss σ1sin (2φ)2(4.22)We can get the same thing from the Mohr’s circle construction to redefine thepaxes by a rotation of φ. The shear stress is simply the radius of the circle (φ1 /2in this case) multiplied by sin (2φ). Mohr’s circle also gives us the normalstresses:pσ11 σ22 σ12pσ12p σ12pσ12cos (2φ)(4.23)cos (2φ)The untransformed 2-dimensional stress tensor looks like this: [σ] pσ10 00(4.24)The tra

332: Mechanical Behavior of Materials Department of Materials Science and Engineering Northwestern University April 20, 2022 Contents 1 Catalog Description4 2 Course Outcomes4 . strength, s f, to separate materials on the y axis. When the story begins, all we had to work with are the materials we could find around us or dig out of