Ryan Tibshirani Data Mining: 36-462/36-662 March 26 2013

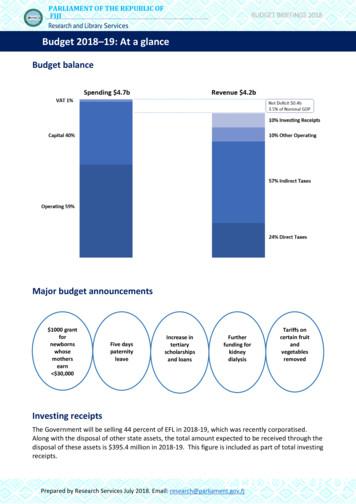
Model selection and validation 1: Cross-validationRyan TibshiraniData Mining: 36-462/36-662March 26 2013Optional reading: ISL 2.2, 5.1, ESL 7.4, 7.101

Reminder: modern regression techniquesOver the last two lectures we’ve investigated modern regressiontechniques. We saw that linear regression has generally low bias(zero bias, when the true model is linear) but high variance,leading to poor predictions. These modern methods introducesome bias but significantly reduce the variance, leading to betterpredictive accuracyGiven a response y Rn and predictors X Rn p , we can thinkof these modern methods as constrained least squares:β̂ argmin ky Xβk22 subject to kβkq t,β RpPpIq 1 gives the lasso (and kβk1 j 1 βj )Iq 2 gives ridge regression (and kβk2 qPp2j 1 βj )2

Regularization at largeMost other modern methods for regression can be expressed asβ̂ argmin ky Xβk22 subject to R(β) t,β Rpor equivalently,β̂ argmin ky Xβk22 λ · R(β).β RpThe term R is called a penalty or regularizer, and modifying theregression problem in this way is called applying regularizationIRegularization can be applied beyond regression: e.g., it canbe applied to classification, clustering, principal componentanalysisIRegularization goes beyond sparsity: e.g., design R to inducesmoothness or structure, instead of pure sparsity3

Example: smoothing splinesSmoothning splines use a form of regularization:fˆ argminnXf 2yi f (xi ) λ ·i 1Z 2f 00 (x) dx{z} R(f ) 0.00.20.41210 0.8λ too small1.00.00.20.4 6 0.6 46 8108 242 4 26 0810 0 01212Example with n 100 points: 0.60.8λ just right1.00.00.20.40.60.81.0λ too big4

Choosing a value of the tuning parameterEach regularization method has an associated tuning parameter:e.g., this was λ in the smoothing spline problem, and λ for lassoand ridge regression in the penalized forms (or t in the constrainedforms)The tuning parameter controls the amount of regularization, sochoosing a good value of the tuning parameter is crucial. Becauseeach tuning parameter value corresponds to a fitted model, we alsorefer to this task as model selectionWhat we might consider a good choice of tuning parameter,however, depends on whether our goal is prediction accuracy orrecovering the right model for interpretation purposes. We’ll coverchoosing the tuning parameter for the purposes of prediction;choosing the tuning parameter for the latter purpose is a harderproblem5

Prediction error and test errorOur usual setup: we observeyi f (xi ) i ,i 1, . . . nwhere xi Rp are fixed (nonrandom) predictor measurements, f isthe true function we are trying to predict (think f (xi ) xTi β fora linear model), and i are random errorsWe call (xi , yi ), i 1, . . . n the training data. Given an estimatorfˆ built on the training data, consider the average prediction errorover all inputs Xn 210ˆˆyi f (xi )PE(f ) Eni 1where yi0 f (xi ) 0i , i 1, . . . n are another set of observations,independent of y1 , . . . yn6

Suppose that fˆ fˆθ depends on a tuning parameter θ, and wewant to choose θ to minimize PE(fˆθ )If we actually had training data y1 , . . . yn and test data y10 , . . . yn0(meaning that we don’t use this to build fˆθ ) in practice, then wecould simply useTestErr(fˆθ ) n 21X 0yi fˆθ (xi )ni 1called the test error, as an estimate for PE(fˆθ ). The larger that nis, the better this estimateWe usually don’t have test data. So what to do instead?7

What’s wrong with training error?It may seem liken 21X 0ˆyi fˆθ (xi )andTestErr(fθ ) ni 1n 21XˆTrainErr(fθ ) yi fˆθ (xi )ni 1shouldn’t be too different—after all, yi and yi0 are independentcopies of each other. The second quantity is called the trainingerror: this is the error of fˆ as measured by the data we used tobuild itBut actually, the training and test error curves are fundamentallydifferent. Why?8

Example: smoothing splines (continued)Back to our smoothing spline example: for a small value of thetuning parameter λ, the training and test errors are very different104 12 0.20.40.60.81.0 0.0 6 2 4 26 08 10 0TestError 1.834812TrainError 0.2210.00.20.40.60.81.09

Training and test error curves, averaged over 100 simulations:2468Training errorTest error1e 071e 051e 031e 01λ10

Cross-validationCross-validation is a simple, intuitive way to estimate predictionerror1.5Prediction error1.00.50.0Even if θ is a continuous parameter, it’s usually not practically feasible to consider all possible valuesof θ, so we discretize the rangeand consider choosing θ over somediscrete set {θ1 , . . . θm }2.02.5Given training data (xi , yi ), i 1, . . . n and an estimator fˆθ ,depending on a tuning parameter θ 2 46 8 10θ11

For a number K, we split the training pairs into K parts or “folds”(commonly K 5 or K 10)K-fold cross validation considers training on all but the kth part,and then validating on the kth part, iterating over k 1, . . . K(When K n, we call this leave-one-out cross-validation, becausewe leave out one data point at a time)12

K-fold cross validation procedure:I Divide the set {1, . . . n} into K subsets (i.e., folds) of roughlyequal size, F1 , . . . FKI For k 1, . . . K:I Consider training on (x , y ), i / Fk , and validating oni i(xi , yi ), i FkI For each value of the tuning parameter θ {θ , . . . θ },1mcompute the estimate fˆθ k on the training set, and recordthe total error on the validation set:X 2ek (θ) yi fˆθ k (xi )i FkIFor each tuning parameter value θ, compute the average errorover all folds,KCV(θ) K 21XX1Xyi fˆθ k (xi )ek (θ) nnk 1k 1 i Fk13

2.5Having done this, we get a cross-validation error curve CV(θ) (thiscurve is a function of θ), e.g.,2.0 1.51.0 0.5CV error 0.0 2 46810θand we choose the value of tuning parameter that minimizes thiscurve,θ̂ argmin CV(θ)θ {θ1 ,.θm }14

Example: choosing λ for the lassoRecall our running example from last time: n 50, p 30, andthe true model is linear with 10 nonzero coefficients. We considerβ̂ lasso argmin ky Xβk22 λkβk1β Rpand use 5-fold cross-validation to choose λ. Sample code formaking the folds:K 5i.mix sample(1:n)folds vector(mode "list",length K)# divide i.mix into 5 chunks of size n/K 10, and# store each chunk in an element of the folds list folds[[1]][1] 30 29 4 2 50 42 27 25 23 41[[2]][1] 21 44 45.9 10 26 166 24 4815

4.0We consider the values: lam seq(0,12,length 60). Theresulting cross-validation error curve:3.5 λ 3.458 3.0 2.5 2.0 1.5CV error 0246λ8101216

1.74.0How does this compare to the prediction error curve? Because thisis a simulation, we can answer this question λ 4.0683.5 3.0 2.5 1.5 2.0 1.41.5CV error 1.6 Prediction error λ 3.4580246λ81012024681012λ17

Standard errors for cross-validationOne nice thing about K-fold cross-validation (for a small K n,e.g., K 5) is that we can estimate the standard deviation ofCV(θ), at each θ {θ1 , . . . θm }First, we just average the validation errors in each fold:CVk (θ) 21 X1yi fˆθ k (xi )ek (θ) nknki Fkwhere nk is the number of points in the kth foldWe then compute the sample standard deviation of CV1 (θ), . . .CVK (θ),q SD(θ) var CV1 (θ), . . . CVK (θ)Finally we estimate the standard deviation of CV(θ)—calledthe standard error of CV(θ)—by SE(θ) SD(θ)/ K18

Example: choosing λ for the lasso (continued)4.0The cross-validation error curve from our lasso example, with standard errors:3.5 λ 3.458 3.0 2.5 2.0 1.5CV error 0246λ8101219

The one standard error ruleThe one standard error rule is an alternative rule for choosing thevalue of the tuning parameter, as opposed to the usual ruleθ̂ argmin CV(θ)θ {θ1 ,.θm }We first find the usual minimizer θ̂ as above, and then move θ inthe direction of increasing regularization (this may be increasing ordecreasing θ, depending on the parametrization) as much as wecan, such that the cross-validation error curve is still within onestandard error of CV(θ̂). In other words, we maintainCV(θ) CV(θ̂) SE(θ̂)Idea: “All else equal (up to one standard error), go for the simpler(more regularized) model”20

Example: choosing λ for the lasso (continued)4.0Back to our lasso example: the one standard error rule chooses alarger value of λ (more regularization):One standard error rule: λ 6.3053.5 Usual rule: λ 3.458 3.0 2.5 2.0 1.5CV error 0246λ8101221

What happens if we really shouldn’t be shrinking in the first place?We’d like cross-validation, our automated tuning parameterselection procedure, to choose a small value of λ λ 0.407 2.5 Prediction error8 λ 0.407 6 2.0 4CV error103.012Recall our other example from last time: n 50, p 30, and thetrue model is linear with all moderately large coefficients 0 246λ81012024681012λ22

12The standard errors here reflect uncertainty about the shape of theCV curve for large λUsual rule: λ 0.4078CV error10One standard error rule: λ 1.017 6 4 0 24681012λThe one standard error rule doesn’t move much from the minimum23

Prediction versus interpretationRemember: cross-validation error estimates prediction error at anyfixed value of the tuning parameter, and so by using it, we areimplicitly assuming that achieving minimal prediction error is ourgoalChoosing λ for the goal of recovering the true model, for the sakeof interpretation, is somewhat of a different task. The value of theparameter that achieves the smallest cross-validation error oftencorresponds to not enough regularization for these purposes. Butthe one standard error rule is a step in the right directionThere are other (often more complicated) schemes for selecting avalue of the tuning parameter for the purposes of true modelrecovery24

Recap: cross-validationTraining error, the error of an estimator as measured by the dataused to fit it, is not a good surrogate for prediction error. It justkeeps decreasing with increasing model complexityCross-validation, on the other hand, much more accurately reflectsprediction error. If we want to choose a value for the tuningparameter of a generic estimator (and minimizing prediction erroris our goal), then cross-validation is the standard toolWe usually pick the tuning parameter that minimizes thecross-validation error curve, but we can also employ the onestandard error rule, which helps us pick a more regularized model25

Next time: model assessment, more cross-validation12How would we do cross-validation for a structured problem likethat solved by smoothing splines? 810 6 42 0 0.00.20.40.60.81.026

Model selection and validation 1: Cross-validation Ryan Tibshirani Data Mining: 36-462/36-662 Ma