Chapter 1 1111----1111 Overview Overview What Is .
Chapter 1Introduction to Statistics1- 1Slide 1OverviewWhat is Statistics about?Slide 2In a Nutshell:Click on the bars to advance to that1-1specificReviewandPreviewpartof thelesson1-21-31-41-5Statistical ThinkingTypes of DataCritical ThinkingCollecting Sample DataSlide 3Slide 4The Three Major Parts of StatisticsProducing Data (details are coming later) In statistics we need data to work with. Data can come from many sources:Producing DataExploratory Data AnalysisInferenceSlide 5Exploratory Data Analysis (details are cominglater)11measurements, surveys, experiments,observational studies, etc. Weaknesses in data production account formost erroneous conclusions in statisticalstudies, therefore the production of good datarequires careful planning.Inference (details are coming later) Once we have our data, we want to knowwhat might be “in there”. Data have a story totell, and our goal is to uncover that story. The statistical process called ExploratoryData Analysis (EDA) employs a variety oftechniques to maximize insight into a data set.It includes some graphical and non-graphicaltechniques to analyze data. When you taste a spoonful of your coffeeand conclude that it needs more sugar,that's an inference. If there's a lot of sugar sitting on thebottom because you were too sleepy tostir it, coffee from the surface won't berepresentative, and you'll end up with anincorrect inference (and a coffee with toomuch sugar). But if you stir your coffeethoroughly before you taste, your spoonfulof data can tell you about the whole cup ofcoffee.Slide 6
Population ExamplesSlide 7 Data: observations (such as measurements, genders, survey responses)Slide 8 All runners in the 2009 L.A. Marathonthat have been collected. All kindergarten kids at a school district Population: the complete collection of all elements (scores, people, All 16 oz. bottled water manufactured by Evianmeasurements, and so on) to be studied. All Milano cookies made by Pepperidge Farm Census: the collection of data from every member of the population. All rats in the biology lab at CSUN Sample: a sub-collection of elements drawn from a population. All ships arriving to the Long Beach port at a particular day All purebred German Shepherd dogs in Los Angeles county All tires made by Good Year All lattes made at the Starbucks closest to your home in a month All rainy days in Los AngelesCopyright 2004 Pearson Education, Inc.Slide 9Slide 10OK, we have a population. Then what?Or We want to learn something about the population.Let’s say our population of interest is ALL runners in the2009 L.A. Marathon.Let’s say our population of interest is ALL kindergartenkids at a school district.We might be interested in the average vocabulary score of ALL kindergarten kids at theschool the proportion of ALL kindergarten kids who live in a singleparent home the mean height of ALL kindergarten kids at the school the percent of ALL kindergarten kids who need speechtherapyWe might be interested in the average age of ALL runners the proportion of ALL runners who completed the marathonunder three hours the percent of female runners who completed the marathon the proportion of runners who are over the age of 50 the mean time of ALL runners who completed the marathon22Slide 11Parameter of interest A parameter is a NUMBER describing somecharacteristic of a population. As the goal ofinference, we wish to estimate this number, ortest a hypothesized value of it. In this course we only consider two parameters of interest Mean ProportionThe director of Personnel for a large firmhas been assigned the task of developing aprofile of the company’s 3500 managers. A couple of characteristics of interestare: Average salary of ALL managers, µ The proportion who have completed the Notation: Population mean: µ Population proportion: pSlide 12ExampleBOTH are PARAMETERS!management training program, p
Slide 13Slide 14Our Goal in InferenceBut. The population we are interested in is usually too big. Inference teaches you what to do in this case. Inference is mainly concerned with the rules or logic of how theresults of a relatively small sample from a large populationcould be used to make inferences about the population. Let’s get back to our keywords.If ALL the populations, whatever we are interested in, wouldbe manageable in size, we would just figure out thepopulation parameter. Then there would be no need forinference.SampleSlide 15Slide 16Important note about the sample When the population is too big (ex.: all adults in the U.S)to find our parameter of interest, we have to take a sampleform the population. Then we can use the sample result tomake conclusions about the population parameter. Thisprocess is called INFERENCE.33The sample must be randomlyselected from the population. Ifsample data are not collected in anappropriate way, the data may be socompletely useless that no amountof statistical torturing can salvagethem.Copyright 2004 Pearson Education, Inc.Slide 17Sample or not sample? Let’s say our population of interest is ALL the members of theU.S. Senate, and our parameters of interest are the proportion of female Senates, p the average age of ALL members, µ Since there are only 100 Senate members, the population isrelatively small, so we don’t need to take a sample to estimate ourparameters of interest. We can just look at them and see whatpercent of them are females, and we can find the average age ofALL members.Slide 18Sample or not sample? A health advocacy agency suspects that the mean level ofacetaminophen (an active ingredient in pain relievers, andcold medications) manufactured by a certain company is notthe advertised value.It is impossible to measure the amountof acetaminophen in ALL the pills madeby this company, and therefore the meanacetaminophen level in ALL pills remains unknown.The agency will need to take a sample of pills, andmeasure the amount of acetaminophen in those pills.
Slide 19Sample statisticExample A statistic is a NUMBER describing some characteristic of asample. Notation: Sample mean:In random sample of 200 people from theSlide 20U.S. 12 people had blood type 0. That’s6% of the sample. This number was a littlesurprising because we know that about 4%of all people in the U.S. has blood type 0. What is the population of interest? All people in the U.S.x Sample proportion: What is the parameter of interest?BOTH are STATISTICS!p The proportion (percent) of ALL people inthe U.S. with blood type 0, which is 4%.With notation: p 4% What is the sample? The 200 randomly selected peopleinference What is the statistic? The proportion (percent) of the 200 peoplewho had blood type 0, which is 6%. Withnotation: p 6%Population/Sample/Parameter/StatisticSlide 22The Basic Idea of InferenceSlide 21Population44Section 1-3Types of DataData ProductionParameterStatisticInferencea numerical measurementdescribing somecharacteristic of apopulationTypes of DataSamplea numerical measurementdescribing somecharacteristic of a sampleSlide 23Slide 24Types of Data Once we have our random sample, we want to collect data fromthem.DataCategorical Some data sets consists of numbers:QuantitativeDiscreteContinuous Age in yearsHeight in inchesWeight in poundsDistance traveled in miles Some data sets consists of non-numerical answers: Eye colorGenderYes/no answersCourse grades
DataSlide 26Slide 25Examples: Categorical dataQuantitative Some of these can beCategorical Gender You can sort the data into a Yes/no questions“boxes”measured ColorMale Satisfaction levelFemale Grade received at the end of the semester The average makes sense Type of car (small, midsize, full size) The average doesn’t make The average distance, oraverage height makes sense Zipcodesense Ethnicity The average eye-color, oraverage gender doesn’t makesenseQuantitative DataSlide 27Examples: Quantitative dataDiscrete Quantitative data: WeightHeightDistanceTimepH levelAmount of moneyGPAAmount of chemical ingredientAgePulse rateLevels of Measurement55Example: The number ofeggs that hens lay.Slide 29Another way to classify data is to use levels ofmeasurement. Four of these levels are discussed in thefollowing slides. Nominal level: categories only Ordinal level: categories with some order Interval level: meaningful differences but no naturalstarting point Ratio level: meaningful differences and a naturalstarting pointCopyright 2004 Pearson Education, Inc.When the number ofpossible values is either afinite number or a‘countable’ number ofpossible values.0, 1, 2, 3, . . .Slide 28ContinuousWhen data result frominfinitely many possible valuesthat correspond to somecontinuous scale that covers arange of values without gaps,interruptions, or jumps.Example: The amount of milkthat a cow produces; e.g. 2.34gallons per day.Nominal Level of MeasurementSlide 30Characterized by data that consist of names, labels, orcategories only. The data cannot be arranged in an orderingscheme (such as low to high).Examples:Survey responses of yes, no, undecidedPolitical affiliationCopyright 2004 Pearson Education, Inc.
Slide 31Slide 32Interval Level of MeasurementOrdinal Level of MeasurementLikeInvolves data that may be arranged in some order, butthe ordinal level, with the additional property that the differencebetween any two data values is meaningful. However, there is nodifferences between data values either cannot be determined ornatural zero starting point (where none of the quantity is present)are meaninglessExamples:Years 1000, 2000, 1776, and 1492Body temperatureExample:Course grades A, B, C, D, or FRanks of collegesCopyright 2004 Pearson Education, Inc.Copyright 2004 Pearson Education, Inc.Slide 33Slide 34Ratio Level of MeasurementThe interval level modified to include the natural zero startingpoint (where zero indicates that none of the quantity is present).For values at this level, differences and ratios are meaningful.Examples:Prices of college textbooks ( 0 represents no cost)Distance traveled by cars (0 milerepresents no distance traveled)66Section 1-4Critical ThinkingCopyright 2004 Pearson Education, Inc.Slide 35Slide 36Misuses of Statistics Bad Samples Refusals Small Samples Correlation & Causality Misleading Graphs Self Interest Study Pictographs Precise Numbers Distorted Percentages Partial Pictures Loaded Questions Deliberate Distortions Order of QuestionsCopyright 2004 Pearson Education, Inc.Section 1-5Collecting Sample Data
Major PointsDefinitionsSlide 37Slide 38 Observational Study If sample data are not collected in anappropriate way, the data may be socompletely useless that no amount ofstatistical tutoring can salvage them.observing and measuring specificcharacteristics without attempting to modifythe subjects being studied Experiment Randomness typically plays a criticalrole in determining which data tocollect.apply some treatment and then observe itseffects on the subjectsCopyright 2004 Pearson Education, Inc.Observational StudyCopyright 2004 Pearson Education, Inc.Slide 39Confounding Cross Sectional StudyData are observed, measured, and collected at onepoint in time.77 Retrospective StudyData are collected from the past by going back intime.Slide 40occurs in an experiment when theexperimenter is not able to distinguishbetween the effects of different factorsTry to plan the experiment soconfounding does not occur! Prospective StudyData are collected in the future from groupssharing common factors.Copyright 2004 Pearson Education, Inc.Experiments: Controlling Effectsof Variables Blindingsubject does not know he or she is receiving atreatment or placebo Blocksgroups of subjects with similar characteristics Completely Randomized Experimental Designsubjects are put into blocks through a process ofrandom selection Rigorously Controlled Designsubjects are very carefully chosenCopyright 2004 Pearson Education, Inc.Copyright 2004 Pearson Education, Inc.Slide 41Replication andSample SizeSlide 42 Replicationrepetition of an experiment when there areenough subjects to recognize the differences indifferent treatments Sample Sizeuse a sample size that is large enough to see the truenature of any effects and obtain that sample using anappropriate method, such as one based onrandomnessCopyright 2004 Pearson Education, Inc.
Methods of SamplingConvenience Sampling(biased sampling method)Slide 43Slide 44use results that are easy to getGOOD SAMPLINGMETHODSBIASED SAMPLINGMETHODS Random Convenience Systematic Voluntary response Stratified ClusterCopyright 2004 Pearson Education, Inc.Voluntary response sampling(biased sampling method)Copyright 2004 Pearson Education, Inc.Good sampling methods:Slide 45Slide 46Probability or random sampling: Individuals are randomlyIndividuals choose to be involvedselected. No one group should be over-represented.Sampling randomly gets rid of bias.88Random samples rely on the absoluteobjectivity of random numbers. There arebooks and tables of random digits availablefor random sampling.DefinitionsSlide 47 Random Samplemembers of the population are selected insuch a way that each individual member has an equalchance of being selected Simple Random Sample (of size n)subjects selected in such a way that everypossible sample of the same size n has the samechance of being chosenCopyright 2004 Pearson Education, Inc. Random SampleSlide 48members of the population are selected insuch a way that each individual member has an equalchance of being selected Simple Random Sample (of size n)subjects selected in such a way that everypossible sample of the same size n has the samechance of being chosen
Random SamplingSystematic SamplingSlide 49Select some starting point and thenselect every Kth element in the populationselection so that each has anequal chance of being selectedCopyright 2004 Pearson Education, Inc.Stratified SamplingSlide 50Copyright 2004 Pearson Education, Inc.Cluster SamplingSlide 51subdivide the population into atleast two different subgroups that share the samecharacteristics, then draw a sample from each subgroup(or stratum)Slide 52divide the population into sections(or clusters); randomly select some of those clusters; chooseall members from selected clusters99Copyright 2004 Pearson Education, Inc.Definitions Copyright 2004 Pearson Education, Inc.Slide 53Sampling Errorthe difference between a sample result and the true populationresult; such an error results from chance sample fluctuations Caution about sampling surveysSlide 54 Nonresponse: People who feel they have something to hideor who don’t like their privacy being invaded probably won’tanswer. Yet they are part of the population. Response bias: Fancy term for lying when you think youNonsampling Errorsample data that are incorrectly collected, recorded, or analyzed(such as by selecting a biased sample, using a defectiveinstrument, or copying the data incorrectly)should not tell the truth. Like if your family doctor asks:“How much do you drink?” Or a survey of female studentsasking: “How many men do you date per week?” People alsosimply forget and often give erroneous answers to questionsabout the past. Wording effects: Questions worded like “Do you agree that itis awful that ” are prompting you to give a particularresponse.Copyright 2004 Pearson Education, Inc.
Slide 55UndercoverageSlide 56Learning about populations from samplesUndercoverage occurs when parts of thepopulation are left out in the process of choosingthe sample.The techniques of inferential statistics allow us to drawBecause the U.S. Census goes “house to house,” homelesspeople are not represented. Illegal immigrants also avoid beingcounted. Geographical districts with a lot of undercoveragetend to be poor ones. Representatives from richer areastypically strongly oppose statistical adjustment of the census.inferences or conclusions about a population from a sample. Your estimate of the population is only as good as yoursampling design Work hard to eliminate biases. Your sample is only an estimate—and if you randomlyHistorically, clinical trials have avoided includingwomen in their studies because of their periods andthe chance of pregnancy. This means that medicaltreatments were not appropriately tested for women.This problem is slowly being recognized andaddressed.sampled again, you would probably get a somewhatdifferent result. The bigger the sample the better.101010
Chapter 1 Slide 1 Introduction to Statistics Click on the bars to advance to that 1-1 Review and Previewspecific part of the lesson 1-2 Statistical Thinking 1-3 Types of Data 1-4 Critical Thinking 1-5 Collecting Sample Data Slide 2 1111----1111 Overview Overview What is Statistics about? In a Nutshell: Slide 3 The Three Major Parts of .
Part One: Heir of Ash Chapter 1 Chapter 2 Chapter 3 Chapter 4 Chapter 5 Chapter 6 Chapter 7 Chapter 8 Chapter 9 Chapter 10 Chapter 11 Chapter 12 Chapter 13 Chapter 14 Chapter 15 Chapter 16 Chapter 17 Chapter 18 Chapter 19 Chapter 20 Chapter 21 Chapter 22 Chapter 23 Chapter 24 Chapter 25 Chapter 26 Chapter 27 Chapter 28 Chapter 29 Chapter 30 .
TO KILL A MOCKINGBIRD. Contents Dedication Epigraph Part One Chapter 1 Chapter 2 Chapter 3 Chapter 4 Chapter 5 Chapter 6 Chapter 7 Chapter 8 Chapter 9 Chapter 10 Chapter 11 Part Two Chapter 12 Chapter 13 Chapter 14 Chapter 15 Chapter 16 Chapter 17 Chapter 18. Chapter 19 Chapter 20 Chapter 21 Chapter 22 Chapter 23 Chapter 24 Chapter 25 Chapter 26
remains, the subnet mask bits define the subnet portion. Whatever bits remain define the host portion. Address 172.16.5.72 1010 1100 0001 0000 0000 0101 0100 1000 Subnet mask 255.255.255.192 1111 1111 1111 1111 1111 1111 1100 0000 Class Net Host First Octet Standard Mask Binary A B C N.H.H.H N.N.H.H N.N.N.H 1-126 128-191 192-223
DEDICATION PART ONE Chapter 1 Chapter 2 Chapter 3 Chapter 4 Chapter 5 Chapter 6 Chapter 7 Chapter 8 Chapter 9 Chapter 10 Chapter 11 PART TWO Chapter 12 Chapter 13 Chapter 14 Chapter 15 Chapter 16 Chapter 17 Chapter 18 Chapter 19 Chapter 20 Chapter 21 Chapter 22 Chapter 23 .
1-31447 CenterPoint Energy, Inc. 74-0694415 (a Texas corporation) 1111 Louisiana Houston, Texas 77002 (713) 207-1111 1-3187 CenterPoint Energy Houston Electric, LLC 22-3865106 (a Texas limited liability company) 1111 Louisiana Houston, Texas 77002 (713) 207-1111 1-13265 CenterPoint Energy Resources Corp. 76-0511406 (a Delaware corporation) 1111 .
About the husband’s secret. Dedication Epigraph Pandora Monday Chapter One Chapter Two Chapter Three Chapter Four Chapter Five Tuesday Chapter Six Chapter Seven. Chapter Eight Chapter Nine Chapter Ten Chapter Eleven Chapter Twelve Chapter Thirteen Chapter Fourteen Chapter Fifteen Chapter Sixteen Chapter Seventeen Chapter Eighteen
18.4 35 18.5 35 I Solutions to Applying the Concepts Questions II Answers to End-of-chapter Conceptual Questions Chapter 1 37 Chapter 2 38 Chapter 3 39 Chapter 4 40 Chapter 5 43 Chapter 6 45 Chapter 7 46 Chapter 8 47 Chapter 9 50 Chapter 10 52 Chapter 11 55 Chapter 12 56 Chapter 13 57 Chapter 14 61 Chapter 15 62 Chapter 16 63 Chapter 17 65 .
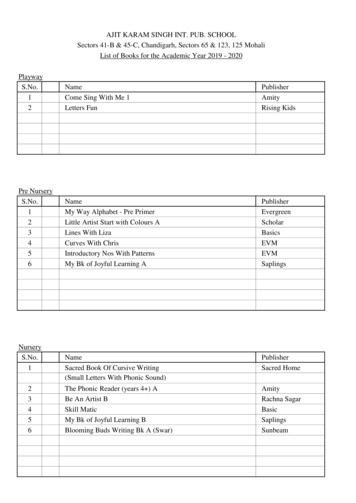
Punjabi 1st Hindi 2nd 1 Suche Moti Pbi Pathmala 4 RK 2 Srijan Pbi Vy Ate Lekh Rachna 5 RK 3 Paraag 1 Srijan. CLASS - 6 S.No. Name Publisher 1 New Success With Buzzword Supp Rdr 6 Orient 2 BBC BASIC 6 Brajindra 3 Kidnapped OUP 4 Mathematics 6 NCERT 5 Science 6 NCERT 6 History 6 NCERT 7 Civics 6 NCERT 8 Geography 6 NCERT 9 Atlas (latest edition) Oxford 10 WOW World Within Worlds 6 Eupheus 11 .