Kontsevich's Noncommutative Numerical Motives
COMPOSITIO MATHEMATICAKontsevich’s noncommutative numerical motivesMatilde Marcolli and Gonçalo TabuadaCompositio Math. 148 (2012), 0437X12000383 Published online by Cambridge University Press
Compositio Math. 148 (2012) ’s noncommutative numerical motivesMatilde Marcolli and Gonçalo TabuadaAbstractIn this article we prove that Kontsevich’s category NCnum (k)F of noncommutativenumerical motives is equivalent to the one constructed by the authors in [Marcolli andTabuada, Noncommutative motives, numerical equivalence, and semisimplicity, Amer.J. Math., to appear, available at arXiv:1105.2950]. As a consequence, we conclude thatNCnum (k)F is abelian semi-simple as conjectured by Kontsevich.1. Introduction and statement of resultsOver the past two decades Bondal, Drinfeld, Kaledin, Kapranov, Kontsevich, Van den Bergh,and others have been promoting a broad noncommutative (algebraic) geometry program where‘geometry’ is performed directly on dg categories; see [BK89, BK90, BV03, Dri02, Dri04, Kal10,Kon98, Kon05, Kon09, Kon10]. Among many developments, Kontsevich introduced a rigidsymmetric monoidal category NCnum (k)F of noncommutative numerical motives (over a groundfield k and with coefficients in a field F ); consult § 4 for details. The key ingredient in his approachis the existence of a well-behaved bilinear form on the Grothendieck group of each smooth andproper dg category.Recently, the authors introduced in [MT11a] an alternative rigid symmetric monoidalcategory NNum(k)F of noncommutative numerical motives; see § 5. In contrast to Kontsevich’sapproach, the authors used Hochschild homology to formalize the ‘intersection number’ in thenoncommutative world.The main result of this article is the following theorem.Theorem 1.1. The categories NCnum (k)F and NNum(k)F are equivalent (as rigid symmetricmonoidal categories).By combining Theorem 1.1 with [MT11a, Theorem 1.9] and [MT11b, Theorem 4.6], we thenobtain the following result.Theorem 1.2. Let k and F be fields of the same characteristic. Then the category NCnum (k)Fis abelian semi-simple.In Theorem 1.2, k and F can be of characteristic zero or of positive characteristic.Assuming several (polarization) conjectures, Kontsevich conjectured Theorem 1.2 in theparticular case where F Q and k is of characteristic zero; see [Kon05]. We observe thatReceived 27 September 2011, accepted in final form 27 April 2012, published online 12 October 2012.2010 Mathematics Subject Classification 18D20 (primary), 18F30, 18G55, 19A49, 19D55 (secondary).Keywords: noncommutative algebraic geometry, noncommutative motives.The first author was partially supported by the NSF grants DMS-0901221, DMS-1007207 and DMS-1201512.The second author was partially supported by the NEC award 2742738 and by the Portuguese Foundation forScience and Technology through PEst-OE/MAT/UI0297/2011 (CMA).This journal is c Foundation Compositio Mathematica 2012.https://doi.org/10.1112/S0010437X12000383 Published online by Cambridge University Press
M. Marcolli and G. TabuadaKontsevich’s beautiful insight not only holds much more generally but, moreover, does not requirethe assumption of any (polarization) conjecture.NotationWe will work over a (fixed) ground field k. The field of coefficients will be denoted by F . Let(C(k), k , k) be the symmetric monoidal category of complexes of k-vector spaces. We will usecohomological notation, i.e. the differential increases the degree.2. Differential graded categoriesA differential graded (dg) category A (over k) is a category enriched over C(k), i.e. the morphismsets A(x, y) are complexes of k-vector spaces and the composition operation satisfies the Leibnizrule d(f g) d(f ) g ( 1)deg(f ) f d(g); consult Keller’s ICM address [Kel06] for furtherdetails.The opposite dg category Aop has the same objects as A, with complexes of morphisms givenby Aop (x, y) : A(y, x). The k-linear category H0 (A) has the same objects as A and morphismsgiven by H0 (A)(x, y) : H0 A(x, y), where H0 denotes 0th cohomology. A right dg A-module M(or simply an A-module) is a dg functor M : Aop Cdg (k) with values in the dg category Cdg (k)of complexes of k-vector spaces. We will denote by C(A) the category of A-modules. Recall from[Kel06, § 3] that C(A) carries a projective model structure. Moreover, the differential gradedstructure of Cdg (k) naturally turns C(A) into a dg category Cdg (A). The dg category Cdg (A)endowed with the projective model structure is a C(k)-model category in the sense of [Hov99,Definition 4.2.18]. Let D(A) be the derived category of A, i.e. the localization of C(A) withrespect to the class of weak equivalences. Its full triangulated subcategory of compact objects(i.e. those A-modules M such that the functor HomD(A) (M, ) preserves arbitrary sums; see[Nee01, Definition 4.2.7]) will be denoted by Dc (A).Notation 2.1. We will denote by Abpe the full dg subcategory of Cdg (A) consisting of thosecofibrant A-modules which become compact in D(A). Since all the objects in C(A) are fibrantand Cdg (A) is a C(k)-model category, we have the natural isomorphisms of k-vector spacesHi Abpe (M, N ) ' HomDc (A) (M, N [ i]),i Z.(1)As any A-module admits a (functorial) cofibrant approximation, we obtain a natural equivalenceof triangulated categories H0 (Abpe ) ' Dc (A).The tensor product A k B of two dg categories is defined as follows: the set of objectsis the Cartesian product of the sets of objects, and the complexes of morphisms are givenby (A k B)((x, x0 ), (y, y 0 )) : A(x, y) k B(x0 , y 0 ). Note that the tensor product of any two dgcategories is automatically derived since we are working over a ground field k. Finally, a A-Bbimodule X is a dg functor X : A k B op Cdg (k) or, in other words, a (Aop k B)-module.Definition 2.2 (Kontsevich [Kon05, Kon98]). A dg category A is smooth if the A-A-bimoduleA( , ) : A k Aop Cdg (k),(x, y) 7 A(y, x)belongs to Dc (Aop k A), and it is proper if for each ordered pair of objects (x, y) we haveXdim Hi A(x, y) .i1812https://doi.org/10.1112/S0010437X12000383 Published online by Cambridge University Press(2)
Kontsevich’s noncommutative numerical motives3. Noncommutative Chow motivesThe rigid symmetric monoidal category NChow(k)F of noncommutative Chow motives, whichwe now recall, was originally constructed (over a commutative ground ring) in [Tab11, Tab05];see [Tab10, § 4] for a survey. Let A, B and C be dg categories. The derived tensor product ofbimodules (see [Dri04, § 14.3]) gives rise to a bi-triangulated functorDc (Aop k B) Dc (B op k C) Dc (Aop k C),(X, Y ) 7 X LB Y.By applying it to the F -linearized Grothendieck group functor K0 ( )F , we then obtain awell-defined bilinear pairingK0 (Aop k B)F K0 (B op k C)F K0 (Aop k C)F ,([X], [Y ]) 7 [X LB Y ].The category NChow(k)F is defined as the pseudo-abelian envelope of the category whose objectsare the smooth and proper dg categories, whose morphisms from A to B are given by theF -linearized Grothendieck group K0 (Aop k B)F , and whose composition operation is given bythe above pairing.In analogy with the commutative world, the morphisms of NChow(k)F are calledcorrespondences. Finally, the symmetric monoidal structure on NChow(k)F is induced by thetensor product of dg categories.4. Kontsevich’s approachIn this section we recall and enhance Kontsevich’s construction of the category NCnum (k)F ofnoncommutative numerical motives; see [Kon05]. Let A be a proper dg category. By construction,the dg category Abpe is also proper and we have a natural equivalence of triangulated categoriesH0 (Abpe ) ' Dc (A). Hence, thanks to the natural isomorphisms (1), we can consider the assignmentobj Dc (A) obj Dc (A) Z,(M, N ) 7 χ(M, N ),where χ(M, N ) is the integerX( 1)i dim HomDc (A) (M, N [ i]).iSince the Grothendieck group K0 (A) of A is the Grothendieck group of the triangulatedcategory Dc (A), a simple verification shows us that the above assignment gives rise to awell-defined bilinear form K0 (A) Z K0 (A) Z. By tensoring it with F , we then obtainχ( , ) : K0 (A)F F K0 (A)F F.(3)The bilinear form (3) is in general neither symmetric nor anti-symmetric. For example, let Aperfbe the dg enhancement Ddg(P1 ) of the derived category Dperf (P1 ) of perfect complexes ofOP1 -modules; see [LO10] for the uniqueness of this enhancement. By construction,perfperfDc (Ddg(P1 )) ' H0 (Ddg(P1 )) ' Dperf (P1 ), and thanks to the work of Beilinson [Bei78] we have HomDperf (P1 ) (O, O(1)[ i]) '1813https://doi.org/10.1112/S0010437X12000383 Published online by Cambridge University Pressk k if i 0,0if i 6 0
M. Marcolli and G. Tabuadaand HomDperf (P1 ) (O(1), O[ i]) 0 for all i Z. Hence, χ([O], [O(1)]) 2 while χ([O(1)], [O]) 0.Now, let us denote byKerL (χ) : {M K0 (A)F χ(M , N ) 0 for all N K0 (A)F },KerR (χ) : {N K0 (A)F χ(M , N ) 0 for all M K0 (A)F }the left and right kernels of the above bilinear form (3). Since (3) is in general not symmetric(nor anti-symmetric), it is expected that KerL (χ) 6 KerR (χ) in some cases, although the authorsdo not know of an example where this nonequality holds. On the other hand, when A is inaddition smooth, we will prove in Theorem 4.3 that KerL (χ) KerR (χ). In order to prove thisresult, let us start by recalling Bondal and Kapranov’snotion of a Serre functor. Let T be aPk-linear Ext-finite triangulated category, i.e. i dim HomT (M, N [ i]) for any two objects M and N in T . Following Bondal and Kapranov [BK89, § 3], a Serre functor S : T T is anautoequivalence together with bifunctorial isomorphismsHomT (M, N ) ' HomT (N, S(M )) ,(4)where ( ) stands for the k-duality functor. Whenever a Serre functor exists, it is unique up toisomorphism.Theorem 4.1. Let A be a smooth and proper dg category. Then the triangulated categoryDc (A) admits a Serre functor.Proof. Note first that the properness of Abpe , the equivalence of categories H0 (Abpe ) ' Dc (A), andthe natural isomorphisms (1) imply that Dc (A) is Ext-finite. By [BK89, Corollary 3.5], it thensuffices to show that Dc (A) is saturated in the sense of [BK89, Definition 2.5]. By combining[CT12, Proposition 4.10] with [Kel06, Theorem 4.12], we observe that every dg category A is dgMorita-equivalent to a dg algebra A. Hence, without loss of generality, we may replace A by A.The fact that Dc (A) is saturated is now the content of [Shk07, Theorem 3.1].2Lemma 4.2. Let A be a smooth and proper dg category and let M, N Dc (A). Then we havethe equalitiesχ(M, N ) χ(N, S(M )) χ(S 1 (N ), M ),where S is the Serre functor given by Theorem 4.1.Proof. Consider the following sequence of equalities:Xχ(M, N ) ( 1)i dim HomDc (A) (M, N [ i])i X X( 1)i dim HomDc (A) (N [ i], S(M ))(5)( 1)i dim HomDc (A) (N, S(M )[i])(6)ii χ(N, S(M )).(7)Equality (5) follows from the bifunctorial isomorphisms (4) and from the fact that a finitedimensional k-vector space and its k-dual have the same dimension. Equality (6) follows from thefact that the suspension functor is an autoequivalence of the triangulated category Dc (A). Finally,equality (7) follows from a reordering of the finite sum which does not alter the sign of eachterm. This shows the equality χ(M, N ) χ(N, S(M )). The equality χ(M, N ) χ(S 1 (N ), M )1814https://doi.org/10.1112/S0010437X12000383 Published online by Cambridge University Press
Kontsevich’s noncommutative numerical motivesis proven in a similar way: simply useHomT (M, N ) ' HomT (S 1 (N ), M ) 2instead of the bifunctorial isomorphisms (4).Theorem 4.3. Let A be a smooth and proper dg category. Then KerL (χ) KerR (χ); theresulting well-defined subspace of K0 (A)F will be denoted by Ker(χ).Proof. We start by proving the inclusion KerL (χ) KerR (χ). Let M be an element of KerL (χ).Since K0 (A)F is generated by the elements of shape [N ], with N Dc (A), it suffices to showthat χ([N ], M ) 0 for every such N . Note that M can be written as [a1 M1 · · · an Mn ] witha1 , . . . , an F and M1 , . . . , Mn Dc (A). We then have the equalitiesχ([N ], M ) a1 χ(N, M1 ) · · · an χ(N, Mn ) a1 χ(M1 , S(N )) · · · an χ(Mn , S(N )) χ(M , [S(N )]),(8)where (8) follows from Lemma 4.2. Finally, since by hypothesis M belongs to KerL (χ), wehave χ(M , [S(N )]) 0 and so conclude that χ([N ], M ) 0. Using the equality χ(M, N ) χ(S 1 (N ), M ) of Lemma 4.2, the proof of the inclusion KerR (χ) KerL (χ) is similar.2Let A and B be two smooth and proper dg categories. Recall that, by definition,HomNChow(k)F (A, B) K0 (Aop k B)F .(9)Since smooth and proper dg categories are stable under tensor product (see [CT12, § 4]), theabove bilinear form (3) (applied to A Aop k B) gives rise toχ( , ) : HomNChow(k)F (A, B) F HomNChow(k)F (A, B) F.By Theorem 4.3 we then obtain a well-defined kernel Ker(χ) HomNChow(k)F (A, B). Thesekernels (one for each ordered pair of smooth and proper dg categories) assemble themselvesinto a -ideal. Moreover, this -ideal extends naturally to the pseudo-abelian envelope, givingrise to a well-defined -ideal Ker(χ) on the category NChow(k)F .Definition 4.4 (Kontsevich [Kon05]). The category NCnum (k)F of noncommutative numericalmotives (over k and with coefficients in F ) is the pseudo-abelian envelope of the quotient categoryNChow(k)F /Ker(χ).Remark 4.5. The fact that Ker(χ) is a well-defined -ideal of NChow(k)F will become clear(er)after the proof of Theorem 1.1.5. Alternative approachThe authors introduced in [MT11a] an alternative category NNum(k)F of noncommutativePnumerical Pmotives. Let A and B be two smooth and proper dg categories, and let X [ i ai Xi ]and Y [ j bj Yj ] be two correspondences. Recall that the Xi are A-B-bimodules, the Yj areB-A-bimodules, and the sums are indexed by a finite set. The intersection number hX · Y i of Xwith Y is given by the formulaX( 1)n ai · bj · dim HHn (A, Xi LB Yj ) 83 Published online by Cambridge University Press
M. Marcolli and G. Tabuadawhere HHn (A, Xi LB Yj ) denotes the nth Hochschild homology group of A with coefficients inthe A-A-bimodule Xi LB Yj . This procedure gives rise to a well-defined bilinear pairingh · i : HomNChow(k)F (A, B) F HomNChow(k)F (B, A) F.(10)As explained in [MT11a, Proposition 4.3], the intersection number hX · Y i agrees with theXYcategorical trace of the composed correspondence A B A in the rigid symmetricmonoidal category NChow(k)F . By standard properties of the categorical trace (see [AK02a,(7.2)]), we then have the equality hX · Y i hY · Xi, where the latter pairing is similar to (10)with A and B interchanged.A correspondence X is said to be numerically equivalent to zero if for every correspondence Ythe intersection number hX · Y i is zero. As proved in [MT11a, Theorem 1.5], the correspondenceswhich are numerically equivalent to zero form a -ideal N of the category NChow(k)F . Thecategory of noncommutative numerical motives NNum(k)F is then defined as the pseudo-abelianenvelope of the quotient category NChow(k)F /N .6. Proof of Theorem 1.1The proof will consist of showing that the -ideals Ker(χ) and N , described in §§ 4 and 5, areexactly the same. As explained in the proof of Theorem 4.1, working with smooth and properdg categories is equivalent to working with smooth and proper dg algebras. In what follows, wewill use the latter approach.Let A be a dg algebra and M a right dg A-module. We will denote by D(M ) its dual,i.e. the left dg A-module Cdg (A)(M, A). This procedure is (contravariantly) functorial in Mand thus gives rise to a triangulated functor D(A) D(Aop )op which restricts to an equivalence Dc (A) Dc (Aop )op . Since the Grothendieck group of a triangulated category is canonicallyisomorphic to the one of the opposite category, we obtain then an induced isomorphism K0 (A)F K0 (Aop )F .Proposition 6.1. Let A and B be two smooth and proper dg algebras and let X, Y Dc (Aop k B). Then χ(X, Y ) F agrees with the categorical trace of the correspondence[Y LB D(X)] HomNChow(k)F (A, A).Proof. The A-B-bimodules X and Y give rise, respectively, to correspondences [X] : A B and[Y ] : A B in NChow(k)F . On the other hand, the B-A-bimodule\D(X) : (Aop k B)pe (X, Aop k B) Dc (B op k A)(see Notation 2.1) gives rise to a correspondence [D(X)] : B A. We can then consider thecomposition[Y ][D(X)][Y LB D(X)] : A B A.(11)Recall from [Tab11] that the -unit of NChow(k)F is the ground field k considered as a dg algebraconcentrated in degree zero. Recall also that the dual of A is Aop and that the evaluation mapevA k Aop k is given by the class [A] K0 (Aop k A)F of A considered as an A-A-bimodule.Hence, the categorical trace of the correspondence (11) is the composition[Y L D(X)][A]Bk Aop k A ' A k Aop k.1816https://doi.org/10.1112/S0010437X12000383 Published online by Cambridge University Press
Kontsevich’s noncommutative numerical motivesSince the composition operation in NChow(k)F is induced by the derived tensor product ofbimodules, the above composition corresponds to the class in K0 (k)F ' F of the complexof k-vector spaces(Y LB D(X)) LAop k A Aop .(12)opNow, note that the complex of k-vector spaces Y k D(X) carries two actions of A and twoactions of B: the actions of Aop are induced by the left action of A on Y and by the right action ofA on D(X), while the actions of B are induced by the right action of B on Y and by the left actionof B on D(X). The coequalizer of the two Aop -actions is given by (Y k D(X)) LAop k A Aop ,which is naturally isomorphic to Y LAop D(X). Similarly, the coequalizer of the two B-actions isgiven by (Y k D(X)) LB op k B B, which is naturally isomorphic to Y LB D(X). The complex ofk-vector spaces (Y LB D(X)) LAop k A Aop is therefore the coequalizer of the Aop - and B-actions,and hence by the above arguments it is naturally isomorphic to Y LAop k B D(X). By combiningthis fact with the natural isomorphism\Y LAop k B D(X) ' (Aop k B)pe (X, Y ),\we deduce that (12) is naturally isomorphic to (Aop k B)pe (X, Y ). As a consequence, these twocomplexes of k-vector spaces have the same Euler characteristic,XX\( 1)i dim Hi ((Y LB D(X)) LAop k A Aop ) ( 1)i dim Hi ((Aop k B)pe (X, Y )).iiThe natural isomorphisms of k-vector spaces (1) (applied to A Aop k B, M X and N Y )then allow us to conclude that the right-hand side of the above equality agrees with χ(X, Y ) Z.On the other hand, the left-hand side is simply the class of the complex (12) in the Grothendieckgroup K0 (k) Z. As a consequence, this equality holds also on the F -linearized Grothendieckgroup K0 (k)F ' F , and so the proof is finished.2Now, let A and B be two smooth and proper dg algebras. As explained above, theduality functor induces an isomorphism K0 (Aop k B)F ' K0 (B op k A)F on the F -linearizedGrothendieck groups. Via the description (9) of the Hom-sets of NChow(k)F , we obtain aninduced duality isomorphism D( ) : HomNChow(k)F (A, B) HomNChow(k)F (B, A).(13)Proposition 6.2. The squareHomNChow(k)F (A, B) F HomNChow(k)F (A, B)χ( , )/F(13) id ' HomNChow(k)F (B, A) F HomNChow(k)F (A, B)h · i/Fis commutative.Proof. Since the F -linearized Grothendieck group K0 (Aop k B)F is generated by the elementsof shape [X], with X Dc (Aop k B), and χ( , ) and h · i are bilinear, it suffices to showthe commutativity of the above square with respect to the correspondences X [X] and Y [Y ].By Proposition 6.1, χ(X, Y ) χ(X, Y ) F agrees with the categorical trace in NChow(k)F ofthe correspondence [Y LB D(X)] HomNChow(k)F (A, A).On the other hand, since the bilinear pairing h · i is symmetric (as explained in § 5), wehave the equality hD(X) · Y i hY · D(X)i. By [MT11a, Corollary 4.4], we then conclude that1817https://doi.org/10.1112/S0010437X12000383 Published online by Cambridge University Press
M. Marcolli and G. Tabuadathe intersection number hY · D(X)i also agrees with the categorical trace of the correspondence[Y LB D(X)]. The proof is then achieved.2We now have all the ingredients needed to prove Theorem 1.1. We will show that acorrespondence X HomNChow(k)F (A, B) belongs to Ker(χ) if and only if it is numericallyequivalent to zero. Assume first that X KerR (χ) Ker(χ). Then, by Proposition 6.2, theintersection number hD(Y ) · Xi is trivial for every correspondence Y HomNChow(k)F (A, B).The symmetry of the bilinear pairing h · i, combined with the isomorphism (13), then allowsus to conclude that X is numerically equivalent to zero.Now, assume that X is numerically equivalent to zero. Once again, the symmetry of thebilinear pairing h · i, together with the isomorphism (13), implies that χ(Y , X) 0 forevery correspondence Y HomNChow(k)F (A, B). As a consequence, X KerR (χ) Ker(χ). Theseresults extend naturally to the pseudo-abelian envelope, and so we conclude that the -idealsKer(χ) and N , described respectively in § 4 and § 5, are exactly the same. This concludes theproof of Theorem 1.1.Remark 6.3. Note that the proof of Theorem 1.1 does not make use of the equality KerL (χ) KerR (χ). If in the proof we replace KerR (χ) by KerL (χ), we would conclude that this latter -ideal also agrees with N . As a consequence, KerL (χ) N KerR (χ), and so we obtain analternative proof of Theorem 4.3.7. An open questionIn this final section, following the suggestion of an anonymous referee, we formulate a precisequestion relating the classical theory of motives with the recent theory of noncommutativemotives. Recall from [MT11c, Proposition 3.1] the construction of the commutative diagramChow(k)F Voev(k)F Num(k)F/ Chow(k)F/ Q(1)R/ NChow(k)F R nil/ NVoev(k)F/ Voev(k)F/ Q(1) / Num(k)F/ Q(1)RN / NNum(k)Fwhere R, R nil and RN are F -linear, additive, symmetric monoidal, and fully faithful functors.Some explanations are in order: Chow(k)F stands for the category of Chow motives, Voev(k)Fstands for the category of Voevodsky’s (pure) motives (i.e. the pseudo-abelian envelope of thequotient of Chow(k)F by the -nilpotence ideal), Num(k)F stands for the category of numericalmotives, and NChow(k)F , NVoev(k)F and NNum(k)F stand for their noncommutative analogues.The categories Chow(k)F/ Q(1) , Voev(k)F/ Q(1) and Num(k)F/ Q(1) are the orbit categoriesassociated to the action of the Tate motive Q(1). Intuitively speaking, the above commutativediagram formalizes the conceptual idea that all the categories of pure motives can be embeddedinto their noncommutative analogues after factoring out by the action of the Tate motive. It isthen natural to ask the following question.Question. Are the functors R, R nil and RN essential surjective (and hence equivalences) underappropriate conditions on k and F ?1818https://doi.org/10.1112/S0010437X12000383 Published online by Cambridge University Press
Kontsevich’s noncommutative numerical motivesIt seems unlikely that the answer to this question will be ‘yes’. Another way of approachingthe possible existence of ‘truly noncommutative motives’ was discussed in [MT11b] in termsof motivic Galois groups of suitable Tannakian categories Num† (k)k and NNum† (k)k ofcommutative or noncommutative numerical motives. In [MT11b] the ‘truly noncommutativemotives’ are identified with the category of representations of the kernel of the surjectivehomomorphismGal(NNum† (k)k ) Ker(t : Gal(Num† (k)k ) Gm )between motivic Galois groups. At present, it is not known whether this surjective homomorphismhas a nontrivial kernel, but this is likely to be the case.AcknowledgementsThe authors are very grateful to Yuri Manin for stimulating discussions and to the anonymousreferees for their comments, corrections and questions, which have greatly improved the ri02Dri04Hov99Kal10Kel06Kon98Kon05Kon09Y. André and B. Kahn, Nilpotence, radicaux et structures monoı̈dales, Rend. Semin. Mat.Univ. Padova 108 (2002), 107–291 (French).Y. André and B. Kahn, Erratum: Nilpotence, radicaux et structures monoı̈dales,Rend. Semin. Mat. Univ. Padova 108 (2002), 125–128 (French).A. Beilinson, Coherent sheaves on Pn and problems in linear algebra, Funktsional. Anal. iPrilozhen. 12 (1978), 68–69 (Russian).A. Bondal and M. Kapranov, Representable functors, Serre functors, and mutations, Izv. Akad.Nauk SSSR Ser. Mat. 53 (1989), 1183–1205.A. Bondal and M. Kapranov, Framed triangulated categories, Mat. Sb. 181 (1990), 669–683(Russian; translation in Sb. Math. 70 (1991), 93–107).A. Bondal and M. Van den Bergh, Generators and representability of functors in commutativeand noncommutative geometry, Mosc. Math. J. 3 (2003), 1–36.D.-C. Cisinski and G. Tabuada, Symmetric monoidal structure on non-commutative motives,J. K-Theory 9 (2012), 201–268.V. Drinfeld, DG categories, Talk in the University of Chicago geometric Langlands seminar,2002, notes available at nglands.html.V. Drinfeld, DG quotients of DG categories, J. Algebra 272 (2004), 643–691.M. Hovey, Model categories, Mathematical Surveys and Monographs, vol. 63 (AmericanMathematical Society, Providence, RI, 1999).D. Kaledin, Motivic structures in noncommutative geometry, in Proceedings of the InternationalCongress of Mathematicians 2010 (Hyderabad, India), vol. II (Hindustan Book Agency, NewDelhi, 2010), 461–496.B. Keller, On differential graded categories, in International Congress of Mathematicians 2006(Madrid), vol. II (European Mathematical Society, Zürich, 2006), 151–190.M. Kontsevich, Triangulated categories and geometry, Course at the École Normale Supérieure,Paris, 1998, notes available at www.math.uchicago.edu/mitya/langlands.html.M. Kontsevich, Noncommutative motives, Talk at the Institute for Advanced Study on theoccasion of the 61st birthday of Pierre Deligne, October 2005, video available athttp://video.ias.edu/Geometry-and-Arithmetic.M. Kontsevich, Notes on motives in finite characteristic, in Algebra, arithmetic, and geometry:in honor of Yu. I. Manin. Vol. II, Progress in Mathematics, vol. 270 (Birkhäuser, Boston, 37X12000383 Published online by Cambridge University Press
M. Marcolli and G. TabuadaKon10M. Kontsevich, Mixed noncommutative motives, Talk at the FRG Workshop on HomologicalMirror Symmetry, University of Miami, 2010, notes available atwww-math.mit.edu/auroux/frg/miami10-notes.LO10V. Lunts and D. Orlov, Uniqueness of enhancement for triangulated categories, J. Amer. Math.Soc. 23 (2010), 853–908.MT11a M. Marcolli and G. Tabuada, Noncommutative motives, numerical equivalence, and semisimplicity, Amer. J. Math., to appear, available at arXiv:1105.2950.MT11b M. Marcolli and G. Tabuada, Noncommutative numerical motives, Tannakian structures, andmotivic Galois groups, Preprint (2011), arXiv:1110.2438.MT11c M. Marcolli and G. Tabuada, Unconditional motivic Galois groups and Voevodsky’s nilpotenceconjecture in the noncommutative world, Preprint (2011), arXiv:1112.5422.Nee01A. Neeman, Triangulated categories, Annals of Mathematics Studies, vol. 148 (PrincetonUniversity Press, 2001).Shk07D. Shklyarov, On Serre duality for compact homologically smooth DG algebras, Preprint (2007),arXiv:math/0702590.Tab05 G. Tabuada, Invariants additifs de dg-catégories, Int. Math. Res. Not. 53 (2005), 3309–3339.Tab10 G. Tabuada, A guided tour through the garden of noncommutative motives, Extended notes ofa survey talk on noncommutative motives given at the 3era Escuela de Inverno Luis SantalóCIMPA: Topics in Noncommutative Geometry, Buenos Aires, July 26 to August 6, 2010, ClayMathematics Proceedings, vol. 16, to appear, available at arXiv:1108.3787.Tab11 G. Tabuada, Chow motives versus noncommutative motives, J. Noncommut. Geom., to appear,arXiv:1103.0200.Matilde Marcolli matilde@caltech.eduDepartment of Mathematics, California Institute of Technology, 253-37 Caltech,1200 E. California Blvd., Pasadena, CA 91125, USAGonçalo Tabuada tabuada@math.mit.eduDepartment of Mathematics, Massachusetts Institute of Technology,Cambridge, MA 02139, USAandDepartamento de Matemática e CMA, FCT-UNL, Quinta da Torre,2829-516 Caparica, 383 Published online by Cambridge University Press
F of noncommutative numerical motives; see x5. In contrast to Kontsevich's approach, the authors used Hochschild homology to formalize the 'intersection number' in the noncommutative world. The main result of this article is the following theorem. Theorem 1.1. The categories NC num(k) F and NNum(k) F are equivalent (as rigid symmetric
(4) Homological algebra: Ext and Tor, global dimension This is the rst course in a master sequence, which continues with: Noncommutative algebra 2. Representations of nite-dimensional algebras Noncommutative algebra 3. Geometric methods. It is also the rst part of a sequence to be given by Henning Krause, which
Five Unifying Themes in Social Psychology 14 Belonging 16 Understanding 18 Controlling 20 Enhancing Seif 22 Trusting 23 Summary of Core Social Motives 25 Culture and the Core Social Motives 26 Summary of Culture and the Core Social Motives 29 Key Features of Social Psychology
From Physics to Number theory via Noncommutative Geometry, II Alain Connes and Matilde Marcolli. Chapter 2 Renormalization, the Riemann{Hilbert correspondence, and motivic Galois theory 1. Contents 2 Renormalization, the Ri
Chapter 5: Related aspects of noncommutative number theory. (with Appendix by Peter Sarnak) 1. The objects of study 1.1. The Riemann zeta function. Riemann formulated his famous hypoth-esis in 1859 in a foundational paper [31], just 8 pages in length, on the number of primes less than a give
\Alain Connes’ noncommutative geometry (.) is a sys-tematic quantization of mathematics parallel to the quanti-zation of physics e ected in the twenties. (.) This theory widens the scope of mathematics in a manner congenial to physics." 2 NCG and di erential forms Connes reinterpr
FUNDAMENTAL SOCIAL MOTIVES 1 Individual Differences in Fundamental Social Motives Rebecca Neel1, Douglas T. Kenrick2, Andrew Edward White2, & Steven L. Neuberg2 1University of Iowa, 2Arizona State University Author Note Rebecca Neel, Department of Psychological and Brain Sciences, University of Iowa.
Open innovation, SMEs, motives for and barriers to cooperation . 4 Open innovation in SMEs: Trends, motives and management challenges 1. INTRODUCTION . product life cycle has turned intellectual property (IP) into an increasingly perishable asset. As a result, a growing number of large MNEs have been moving from an .
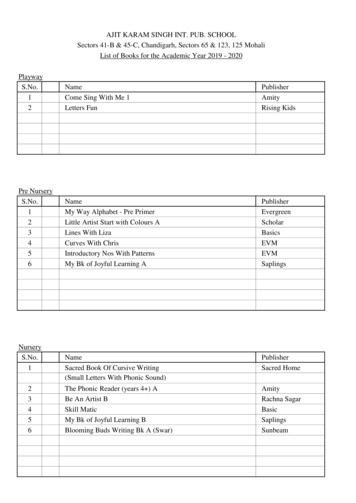
Punjabi 1st Hindi 2nd 1 Suche Moti Pbi Pathmala 4 RK 2 Srijan Pbi Vy Ate Lekh Rachna 5 RK 3 Paraag 1 Srijan. CLASS - 6 S.No. Name Publisher 1 New Success With Buzzword Supp Rdr 6 Orient 2 BBC BASIC 6 Brajindra 3 Kidnapped OUP 4 Mathematics 6 NCERT 5 Science 6 NCERT 6 History 6 NCERT 7 Civics 6 NCERT 8 Geography 6 NCERT 9 Atlas (latest edition) Oxford 10 WOW World Within Worlds 6 Eupheus 11 .