Analytic Analysis Of Galaxy Number Counts
Analytic Analysis of Galaxy NumberCountsMaster Thesisby Cynthia WinterFaculty of Physics,Bielefeld UniversityApril 2016Supervisor and First Referee: Prof. Dr. Dominik SchwarzSecond Referee: Dr. Daniel Boriero
Contents1
1 IntroductionThis master thesis deals with the theoretical investigation and analytical calculation ofsource counts in different cosmological models. Therefore it is dedicated to the questionin how far number counts can be calculated analytically and to what extent they mightbe used in order to investigate cosmological features, for example the cosmic expansiondescribed by the Hubble law, acceleration or deceleration, spatial curvature and theenergy content of the universe which can be composed of various components such asmatter, radiation or some kind of dark energy represented by a cosmological constantterm in the Friedmann equations.Number counts of cosmological objects, i.e. galaxies or clusters of galaxies which aregravitationally unbound and thus obeying the Hubble law, are the simplest statisticsthat can be derived from any survey. Differential number counts correspond to thenumber of objects in a given flux or redshift interval and solid angle of the sky. Integralsource counts are obtained even easier by counting all objects in a given sky area abovesome minimal flux level or up to the sensitivity reached by the observational instrument.Although integral number counts have been commonly used in the past they have thegreat disadvantage that rapid changes of the differential number counts are concealed[1]. Furthermore, integral number counts are not statistical independent for differentflux densities and estimating errors is difficult (see e.g. [2], [3]).Contrary to integral counts, differential number counts can be easily applied to testdifferent cosmological models, especially those modelling cosmic evolution of galaxies.For simple models such as the Einstein model, de Sitter model, Einstein-de Sitter andMilne model, number counts can be calculated completely analytical in the case offrequency independent (bolometric) counts. These models also have the great advantage that the number counts can be expressed analytically as a function of flux densityinstead of redshift. Thus, they could be easily compared to surveys with a vast numberof cosmological objects, for no redshift information is necessary which is often unknownfor many objects. In the case of frequency dependent source counts, i.e. differentialnumber counts in a given frequency interval, there are still analytic solutions for thenumber counts expressed redshift dependently, but for the flux dependent counts analytic solutions only exist for some special values of the spectral index α, otherwiseapproximations have to be made for the low and high redshift regime, respectively.If combinations of these simple models are considered, e.g. the Λ-Cold-Dark-Matter(ΛCDM) model with flat spatial geometry and an energy density consisting of colddark matter and dark energy (k 0, Ω Ωm ΩΛ ) analytic solutions no longer exist,so again approximations are needed or numerical calculations have to be done.3
Figure 1.1: Differential source counts at 150, 325, 408, 610 MHz normalised to cSν 2.5 ,with c 1000, 100, 10 and 1, respectively (Figure taken from [4])The basis for all calculations in this thesis are the Friedmann equations, which are obtained from Einstein’s field equations and the Friedmann-Lemaitre-Robertson-Walker(FLRW)-metric, which will be layed out in the second chapter. Sources will be assumed to be point-like with equal luminosities and distributed uniformly throughoutspace. For the calculation of the differential number counts, first the number of objectper solid angle and distance interval is given and then expressed for a redshift intervalin the case of expanding models. Then the number counts per solid angle and fluxinterval are calculated and the result is expressed in terms of the flux. Traditionally,the result is normalised to the source counts expected in a static Euclidean universefor comparison. Comparing the results with data, one would see immediately that evolutionary effects result in a different behaviour than the calculated one, where objectsare assumed to be point sources with the same luminosity over all times (e.g. [4]).Figure 1.1 shows an example of differential number counts data at different frequancies together with fits obtained by an evolutionary model from Massardi et al. [4], [5].As for this example, number counts are commonly shown in double logarithmic plots 5/2as a function of flux density and normalised to cSν .In the second chapter, a short introduction to the theoretical basis needed for thecalculation and interpretation of galaxy number counts is given. This chapter includesthe FLRW-metric, the Friedmann equations and cosmological distance measures whichhave to be applied carefully to avoid ambiguities. Then the general procedure of calculating differential and integral number counts is introduced and carried out in general.Finally, the second chapter concludes with a brief outline of the cosmological models4
that will be considered throughout this thesis and some others which are interestingor of historical significance.In the third chapter, the differential and intergral number counts for the static Euclidean model, static Einstein model, de Sitter, Einstein-de Sitter and Milne model arecalculated and compared to each other regarding their special properties such as thelimits for the high and low flux regime. Furthermore, the integral number counts willbe calculated and the effects of model parameters on the sorce counts will be discussed.After that, in chapter four, the specific number counts for the expanding models,i.e. the de Sitter model, Einstein-de Sitter and Milne model will be calculated, asthe frequency bands are redshifted according to the steepness of the spectrum of thesource. Analytic solutions for the frequency dependent case, assuming a spectrumwith a constant spectral index α, can only be found for some special values of α, oftenyielding quite complicated solutions. Therefore a simple but nevertheless accurateapproximation for a wide range of fluxes will be given as well and compared to theexact solutions.Then in the fifth chapter, the number counts for the ΛCDM-model will be consideredand calculated analytically as far as possible. There is an analytic solution to theredshift dependent differential number counts, but this cannot be expressed in termsof elementary functions. In order to find a result for the number counts in a fluxinterval, approximations will be made.Finally, we will summarise the results and give an outlook on the issues that requirefurther investigation or seem interesting for a better understanding of the way in whichfeatures like curvature, energy density and a cosmological constant leave an imprint oncosmology that can be observed via galaxy number counts.5
2 Theoretical foundation andcosmological models2.1 Theoretical foundation2.1.1 FLRW-metricThe basis for all the following calculations is the Friedmann-Lemaitre-Robertson-Walkermetric (FLRW-metric) which follows from the assumptions of spatial homogeneity andisotropy, i.e. the cosmological principle, which is always assumed throughout this thesis.In its most general form the FLRW-metric readsds2 dt2 a(t)2 dΣ2(2.1)(where the speed of light is set equal to 1). For simplicity in the calculations for dΣ2the following conventiondΣ2 dχ2 f 2 (χ)dΩ2(2.2)is used and thus the FLRW-metric is given by ds2 dt2 a2 (t) dχ2 f 2 (χ)dΩ2 ,wheref (χ) sin( k · χ)χpsinh( k · χ) 1k 1 k : k 1: k 0: k 1(2.3)(2.4)with dΩ2 dθ2 sin2 (θ)dφ2 and χ f 1 (r) and the curvature parameter k 1, 0 and-1 standing for positive spatial curvature (spherically, closed universe), zero curvature(open, flat space) and negatively curved space (hyperbolic, open universe), respectively.The FLRW-metric can also be expressed in terms of the radial distance r as dr222222 r dΩ(2.5)ds dt a (t)1 kr2[2]. There are two different conventions regarding the FLRW-metric. On one hand,the curvature can be taken to be dimensionless with the discrete values k 0, 1.Then the distance χ is also dimensionless and the scale factor must have dimensionsof length. On the other hand, the curvature can be taken to have the dimension of1/[length]2 , then the scale factor is dimensionless. Throughout this thesis the firstconvention will be applied.6
2.1.2 Friedmann equationsAll cosmological models considered in this thesis are based on the Friedmann equationswhich are obtained by applying the FLRW-metric to Einstein’s field equation of generalrelativity (see e.g. [6]). The first Friedmann equationH2 k8πGΛ ρ 2a33(2.6)is derived from the 00-component of Einstein’s equation. Here H(t) is the Hubbleparameterȧ(t),(2.7)H(t) a(t)k the curvature parameter, G the gravitational constant, Λ the cosmological constantand ρ ρ(t) denotes the total energy density of the universe at cosmic time t. Fromthe first Friedmann equation together with the trace of Einstein’s field equation followsthe second Friedmann equation, often also referred to as the Friedmann accelerationequationä4πGΛḢ H 2 (ρ 3p) ,(2.8)a33where p denotes the pressure. For the energy density and the pressure it holds thecosmological equation of state of a perfect fluidw pρ(2.9)where w is assumed dimensionless. When applied to the FLRW-metric, the equation of state describes the cosmic evolution of a perfect fluid in an isotropic universe.Regarding the covariant energy-momentum conservation equationρ̇ 3(ρ p)ȧa(2.10)and assuming that w is a constant, the equation of state can be related with the scalefactor viaρ a 3(1 w) .(2.11)These equations will be used in order to derive the properties of the various cosmological models for different curvature and energy contents. Once the main featuresof a cosmological model like curvature, cosmological constant and energy density arespecified, the Friedmann equations can be used to calculate the other properties suchas the Hubble parameter and scale factor.2.1.3 Distance measuresIn cosmology there exist different distance measures according to the way in which theissue is considered. Because of the curvature of space-time there is no unambiguousdistance that can always be applied, but these distance measures become equal tothe Euclidean notion of distance for redshifts close to one. Regarding cosmological7
distances the central assumption which is made is that all observers have the samecosmic age.One of the most important distance measures in cosmology is the redshift z for whichholdsa01 z ,(2.12)awhere a0 denotes the present value of the scale factor [7].A useful distance measure for the calculation of the differential number counts inflat models is the Hubble distance1,H(z)dH (2.13)which corresponds to the age the universe would have if the expansion had been linearin the past.The distance which corresponds to the ’real’ distance between objects is the so calledproper distance, which is the coordinate distance times the scale factor, i.e.Zχdp (t) adχ0 aχ.(2.14)0For an observed light ray (ds2 0) it follows from the FLRW-metric dt dχa(t)(2.15)and the redshift changes with time likedzd(1 z)d(a0 /a) (1 z)H(z).dtdtdt(2.16)Therefore the coordinate distance is given byZt0χ dt1 aa0tZ01 z0dz 0(1 z 0 )H(z 0 )(2.17)zand thus the comoving distance becomesZzdz 0.H(z 0 )(2.18)adc (z)dc (z) .a01 z(2.19)dc (z) a0 χ 0Then the proper distance becomes equal todp (z) Another important distance measure is the luminosity distance dL which is given byrrLPdL .(2.20)4πSS8
The luminosity distance is relevant for obtaining the flux of an object depending on itsredshift and will be used for the calculation of the number counts expressed in termsof the flux. The flux is given byS 4πa20 (1LP 22 z) f (χ)(1 z)2 a20 f 2 (χ)and therefore the luminosity distance for arbitrary curvature becomes dcdL (z) (1 z)a0 f (χ) (1 z)a0 fa0(2.21)(2.22)with 1f (χ) sinkχ .kThus the luminosity distance can be expressed ass!ra20kdc (z) .dL (z) (1 z)sinka20(2.23)(2.24)In flat space, the luminosity distance becomesdL (1 z)dc .Furthermore, another distance measure is the angular diameter distance dcRp (z)11da (z) a(t)f (χ) a0f (χ) a0fθ1 z1 za0(2.25)(2.26)which relates the actual diameter of an object Rp (z) to its angular diameter θ. Withthe luminosity distance the angular diameter distance can be expressed asda (z) 1dL (z).(1 z)2(2.27)This distance measure is not needed for the calculations of differential number countsin this thesis but nonetheless stated here for the sake of completeness.2.1.4 Differential number countsLike already mentioned in the previous chapter, differential or integral number countsare a very simple and practical means for validating cosmological models and screeningthe history of the universe. In order to calculate the number counts, the properties ofthe different cosmological models are applied to the Friedmann equations to derive theunknown parameters which then can be used to obtain the Hubble distance and thecomoving distance. Differential number counts are defined as the number of objects(meaning galaxies or galaxy clusters) in a solid angle dΩ and a distance interval dr ormore general dχ, i.e.dN.dΩdχ9
Since the coordinate distance χ is not an observable quantity and radial distancesare hard to obtain especially for very distant objects, it is more convenient to write thenumber counts for a redshift interval dzdNdN dχ .(2.28)dΩdzdΩdχ dzAs redshift information is also not available for many objects, it is often more practicalto rewrite the differential number counts for a flux interval rather than redshift asfluxes can be “easily” measured. Therefore the quantitydNdN dz dΩdSdΩdz dS(2.29)should be established.The calculation of differential number counts begins with the FLRW-metric (see sec.2.1.1), from which the volume in the solid angle dΩ and coordinate distance intervaldχ can be derived asa30 f 2 (χ)dV3 2 a f (χ) .(2.30)dΩdχ(1 z)2With equation (2.12) for the redshift, equation (2.18) andn(z) n0 (1 z)3 ,(2.31)the differential number counts in a solid angle dΩ and coordinate distance interval dχbecome dNdc (z)3 2 n0 a0 f.(2.32)dΩdχa0The change of the redshift with the coordinate distance is given bydz dta0dz (1 z)H(z) a0 H(z).dχdt dχ1 z(2.33)As the quantity χ cannot be measured it is more convenient to calculate either thedifferential number counts for a redshift or for a flux interval. The differential numbercounts in a redshift interval dz are given by dNdc (z)12 2 n0 a0 f.(2.34)dΩdza0H(z)Then the differential number counts can be expressed as a function of redshift bys!a20kdN1d (z) n0 sin2.(2.35)2 cdΩdzka0H(z)Accordingly, the differential number counts for a flux interval dS can be calculatedusing equation (2.29). Together with equation (2.22) and equation (2.34) the generalsolution for the differential number counts in a frequency interval dS is given by 5 dcf a0 (1 z)3dNn01“ ” .(2.36) dcdf adΩdS2PH(z)dc0f a0 dz (1 z)10
As the calculation of this expression is much simpler using the model dependent soludNtions of the differential number counts in the redshift interval dΩdzand the changingdSdNrate of the flux with redshift dz , the quantity dΩdS will be calculated for each modelseparately in the third chapter via equation (2.29).Differential number counts probe the evolution of the comoving volume and a possibleevolution of the sources, i.e. n0 n0 (z). Unfortunately, for distant objects there is astrong correlation of the number counts to evolution of the sources, i.e. the evolutionof galaxies both in number (galaxies have merged in the past) and their luminosity(galaxies have been more luminous in the past) (e.g. [4]]. Therefore catalogues of verydistant galaxies cannot be directly applied to the calculated differential number countwithout evolutionary models being taken into account.2.1.5 Integral number countsAnother cosmological probe is provided by integral number counts, that is the totalnumber of galaxies above a given flux limitZ dN( Smin ) dΩdNdS,dΩdS(2.37)Sminor up to a given value of redshiftdN( zmax ) dΩzZmaxdNdz.dΩdz(2.38)0Integral number counts have the disadvantage of concealing changes in the numberdensity with the flux. Furthermore the numbers of sources in two neighbouring fluxintervals are not statistically independent from each other. Although integral numbercounts are impractical as a cosmological probe for a comparison of models with data,they can be quite useful for a comparison of different models and their properties,assuming all objects are identical.2.2 Cosmological modelsAll cosmological models considered thoughout this thesis are Friedmann models, whichmeans based on the Friedmann equations and thus on general relativity. As the Friedmann equations are derived from Einstein’s field equation together with the FLRWmetric (see section 2.1), Friedmann models also include the cosmological principle, thatis the assumption of homogeneity and isotropy (e.g. [6]).The first necessary step for deriving a simple model of the universe and its possibleevolution in time, is the cosmological principle, for this gives the simple FLRW-metric.Accordingly, the Hubble law must be valid, because it is the unique expansion lawwhich conserves homogeneity and isotropy (e.g. [12]). Historically, the first attempt infinding a reasonable model for the universe, was to assume that everything was static,for this would simplify the matter enourmously as distances and objects never changed.11
Therefore the simplest cosmological model that can be considered is the static Euclidean universe. This universe is flat and neither expanding nor contracting and thusspace just corresponds to the three-dimensional Euclidean space. That leads to thedifferential number counts being proportional to (S/S0 )5/2 . This model traditionallyserves as a reference for all other models. Moreover, the Euclidean part can be isolated from the flux dependent differential number counts in all models considered inthe third chapter and therefore the remaining factor can be examined seperately. Unfortunately, a static Euclidean universe can only be realized in a spatially infinite andempty universe.Furthermore, a reaonable cosmological model should be compatible with generalrelativity and therefore Einstein’s field equations. This is how the static Einstein modeland with it the cosmological constant came about. Einstein wanted to install a modelof the universe which was both static (temporally infinite) and spatially finite, butto counteract the gravitational attraction of matter he had to propose a cosmologicalconstant keeping a spatially finite universe from collapsing or expanding. Moreover,this model is closed, hence having a spherical spatial geometry with k 1. The energydensity only consists of pressureless “dust” and the cosmological constant, the Hubblerate and redshift are of course zero in a static universe and thus the scale factor isconstant (a a0 ). Unfortunately, this model is highly unstable because even veryslight deviations from the right energy density and cosmological constant or spatialcurvature lead to an expanding or contracting universe (see e.g. [8], [9]).At that time, also another static model was proposed which would also be static witha Euclidean geometry. This model is spatially as well as temporally infinite, thus notneeding a cosmological constant to counteract gravity, and also spatially flat. As thisuniverse is of infinite age and size the light of infinitely many stars had time to reachthe earth and therefore would lead to a bright night sky in contradiction to observation,known as Olbers’ paradox.Another stationary cosmology which was quite popular before the discovery of t
Then in the fifth chapter, the number counts for the ΛCDM-model will be considered and calculated analytically as far as possible. There is an analytic solution to the redshift dependent differential number counts, but this cannot be expressed in terms of elementary functions. In order to find a result for the number counts in a flux
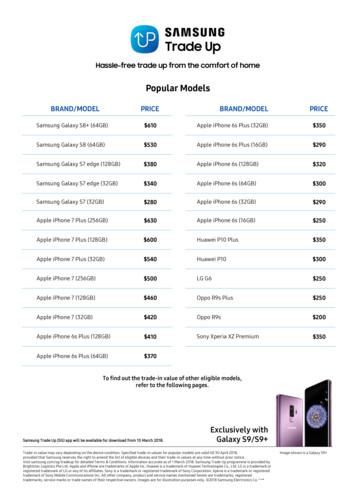
Samsung Galaxy S6 (32GB) 100 Samsung Galaxy S5 60 Samsung Galaxy A9 Pro 250 Samsung Galaxy A8 100 Samsung Galaxy A7 2017 200 Samsung Galaxy A7 2016 130 Samsung Galaxy A7 50 Samsung Galaxy A5 2017 150 Samsung Galaxy A5 2016 100 Samsung Galaxy A5 50 Samsung Galaxy A3 2016 80 Samsung Galaxy
4. Samsung Galaxy Watch Active User Manual Samsung Galaxy Watch Active User Manual - Download [optimized]Samsung Galaxy. 5. Samsung Galaxy Watch Active User Manual Samsung Galaxy Watch Active User Manual - Download [optimized]Samsung Galaxy. 6. SAMSUNG Galaxy Watch Active User Manual Samsung Galaxy Watch Active Quick Start Guide 1 .
Samsung: Galaxy Note 3, Galaxy Note 4, Galaxy S3, Galaxy S3, Galaxy S5, Galaxy S6, Galaxy S7, Galaxy Tab 4 Google : Nexus 5, Nexus 5X, Nexus 6, Nexus 9 . Please refer to section 1.1 of this Product Manual for a list of compatible smart devices for this product. Please make sure you are using a compatible device.
of the screen. Hold down the green key until the Bluetooth symbol starts to blink. . Galaxy Note 5 Galaxy Tab E Galaxy Tab S2 Galaxy Tab 4 Galaxy Grand Neo Galaxy Grand Prime Galaxy E5 Compatible devices Sony Xperia E1 Xperia
24 Galaxy S7 32GB ¹ 0 0 0 0 0 0 25 Galaxy S7 Edge 32GB ¹ 0 0 0 0 0 0 26 Galaxy S7 Edge 128 GB ¹ 0 0 0 0 0 0 27 Galaxy A80 (128GB/8GB) x 170 145 102 85 26 20 28 Galaxy A70 (128GB/6GB) x 150 123 87 73 22 17 29 Galaxy A50 (64GB/4GB) x 80 60 40 30 Ga
Samsung Galaxy Note 10.1 Fast-charge most smartphones & tablets, such as: Nexus 7 Nexus 5 iPhone Samsung Galaxy S 5 Samsung Galaxy Note 10.1 Microsoft Surface Pro 2 Samsung Galaxy Note 4 Microsoft Surface RT Samsung Galaxy S5 Acer Iconia W700P-6821 Samsung Galaxy S4 Windo
LG G3 Smartphone Samsung Galaxy Note 4, Note Edge, Galaxy Alpha, Galaxy Tab S 8.4 LTE & 10.5 LTE Samsung Galaxy S5 with KNOX 2 Samsung Galaxy Note 4, Note Edge, Alpha, Galaxy Tab S 8.4 LTE & 10.5 LTE, Galax
Galaxy S4 Optimus L65 Xperia Z1 Galaxy S4 Active Optimus L70 Xperia Z1 Compact Galaxy S4 Mini Optimus L80 Xperia Z1F Galaxy S5 Optimus L90 Xperia Z1S Galaxy S5 Active Optimus Zone 2 Xperia ZL Galaxy S5 Sport Volt Xperia ZR Vu 3.0 TABLET COMPATIBILITY APPLE SAMSUNG