A Gradient-Descent Method For Curve Fitting On Riemannian . - UCLouvain
Tech. report UCL-INMA-2009.023A Gradient-Descent Method for Curve Fitting onRiemannian Manifolds Chafik Samir†P.-A. Absil†Anuj Srivastava‡Eric Klassen§August 28, 2009AbstractGiven data points p0 , . . . , pN on a manifold M and time instants 0 t0 t1 . . . tN 1, we consider the problem of finding a curve γ on M that best approximates the datapoints at the given instants while being as “regular” as possible. Specifically, γ is expressedas the curve that minimizes the weighted sum of a sum-of-squares term penalizing the lack offitting to the data points and a regularity term defined, in the first case as the mean squaredvelocity of the curve, and in the second case as the mean squared acceleration of the curve.In both cases, the optimization task is carried out by means of a steepest-descent algorithmon a set of curves on M . The steepest-descent direction, defined in the sense of the first-orderand second-order Palais metric, respectively, is shown to admit simple formulas.Keywords: curve fitting, steepest-descent, Sobolev space, Palais metric, geodesic distance,energy minimization, splines, piecewise geodesic, smoothing, Karcher mean.1IntroductionWe are interested in the problem of fitting smooth curves to given sets of points on nonlinearmanifolds. Let p0 , p1 , . . . , pN be a finite set of points on a Riemannian manifold M , and let0 t0 t1 . tN 1 be distinct and ordered instants of time. The problem of fittinga smooth curve γ on M to the given points at the given times involves two goals of conflictingnature. The first goal is that the curve should fit the data as well as possible, as measured, e.g.,by the real-valued function Ed defined by:Ed (γ) NXd2 (γ(ti ), pi ),(1)i 0where d denotes the distance function on the Riemannian manifold M . The second goal is thatthe curve should be sufficiently “regular” in a certain sense, e.g., the changes in velocity or inacceleration should be minimized. We are thus facing an optimization problem with two objectivefunctions—a fitting function Ed and the regularity function Es —whose domain is a suitable setof curves on the Riemannian manifold M .Curve fitting problems on manifolds appear in various applications. To cite but one example,let (Ii )i N be a temporal sequence of images of a 2D or 3D object motion, in which the object This paper presents research results of the Belgian Network DYSCO (Dynamical Systems, Control, and Optimization), funded by the Interuniversity Attraction Poles Programme, initiated by the Belgian State, SciencePolicy Office. The scientific responsibility rests with its authors. This research was supported in part by AFOSRFA9550-06-1-0324 and ONR N00014-09-10664.† Département d’ingénierie mathématique, Université catholique de Louvain, B-1348 Louvain-la-Neuve, Belgium(http://www.inma.ucl.ac.be/{ samir, absil}).‡ Dept of Statistics, Florida State University, Tallahassee, FL 32306, USA (anuj@stat.fsu.edu).§ Dept of Mathematics, Florida State University, Tallahassee, FL 32306, USA (klassen@math.fsu.edu).1
can appear and disappear at arbitrary times due to obscuration and other reasons. The task is toestimate the missing data and recover the motion of the object as well as possible. It is clear thatfocussing on the first goal (fitting the data) without concern for the second goal (regularity of thecurve) would yield poor motion recovery, and that the result is likely to be improved if inherentregularity properties of the object motion are taken into account.1.1Previous workOne possible way of tackling an optimization problem with two objective functions is to turn itinto a classical optimization problem where one of the objective functions becomes the objectivefunction and the other objective function is turned into a constraint.Let us first discuss the case where the fitting objective function Ed is minimized under aregularity constraint. When M Rn , a classical regularity constraint is to restrict the curve γto the family of polynomial functions of degree not exceeding m, (m N ). This least-squaresproblem cannot be straightforwardly generalized to an arbitrary Riemannian manifold M becausethe notion of polynomial does not carry to M in an obvious way. An exception is the case m 1;the polynomial functions in Rn are then straight lines, whose natural generalization on Riemannianmanifolds are geodesics. The problem of fitting geodesics to data on Riemannian manifold M wasconsidered in [MS06] for the case where M is the special orthogonal group SO(n) or the unitsphere Sn .The other case is when a regularity criterion Es is optimized under a constraint on Ed , in whichcase it is natural to impose the interpolation constraint Ed (γ) 0. For example, when M Rn ,minimizing the function Es defined byZ1 12kγ̇(t)k dt(2)Es,1 (γ) 2 0yields the piecewise-linear interpolant for the given data points and time instants (this followsfrom [Mil63, p. 70]), while minimizing1Es,2 (γ) 2Z1kγ̈(t)k2 dt0yields solutions known as cubic splines. (From now on, we will frequently omit the variable t inthe integrand when it is clear from the context.) For the case where M is a nonlinear manifold,several results on interpolation can be found in the literature. Crouch and Silva Leite [CS91] (orsee [CS95]) generalized cubic splines to Riemannian manifolds, defined as curves γ that minimize,under interpolation conditions, the functionZ1 1 D2 γ D2 γEs,2 (γ) dt,(3),2 0dt2 dt2 γ(t)2where Ddt2γ denotes the (Levi-Civita) second covariant derivative and h·, ·ix stands for the Riemannian metric on M at x. (The subscript may be omitted if there is no risk of confusion.)They gave a necessary condition for optimality in the form of a fourth-order differential equation, which generalizes a result of Noakes et al. [NHP89]. Splines of class C k were generalizedto Riemannian manifolds by Camarinha et al. [CSC95]. Still in the context of interpolation onmanifolds, but without a variational interpretation, we mention the literature on splines based ongeneralized Bézier curves, defined by a generalization to manifolds of the de Casteljau algorithm;see [CKS99, Alt00, PN07]. Recently, Jakubiak et al. [JSR06] presented a geometric two-step algorithm to generate splines of an arbitrary degree of smoothness in Euclidean spaces, then extendedthe algorithm to matrix Lie groups and applied it to generate smooth motions of 3D objects. Another approach to interpolation on manifolds consists of mapping the data points onto the affinetangent space at a particular point of M , then computing an interpolating curve in the tangent2
space, and finally mapping the resulting curve back to the manifold. The mapping can be defined,e.g., by a rolling procedure, see [HS07, KDL07].Another way of tackling an optimization problem with two objective functions is to optimize aweighted sum of the objective functions. In the context of curve fitting on manifolds, this approachwas followed by Machado et al. [MSH06] using the first-order smoothing term (2) and by Machadoand Silva Leite [MS06] for the second-order smoothing term (3).Specifically, in [MSH06], the objective function is defined to beN1X 2λE1 d (γ(ti ), pi ) 2 i 02Z1hγ̇, γ̇i dt,0over the class of all piecewise smooth curves γ : [0, 1] M , where λ ( 0) is a smoothingparameter. Solutions to this variational problem are piecewise smooth geodesics that best fit thegiven data. As shown in [MSH06], when λ goes to , the optimal curve converges to a singlepoint which, for certain classes of manifolds, is shown to be the Riemannian mean of the datapoints. When λ goes to zero, the optimal curve goes to a broken geodesic on M interpolating thedata points.In [MS06], the objective function is defined to beNλ1X 2d (γ(ti ), pi ) E2 2 i 02Z01D2 γ D2 γ,dt2 dt2dtover a certain set of admissible C 2 curves. The authors give a necessary condition of optimality thattakes the form of a fourth-order differential equation involving the covariant derivative and the curvature tensor along with certain regularity conditions at the time instants ti , i 0, . . . , N [MS06,Th. 4.4]. The optimal curves are approximating cubic splines: they are approximating because ingeneral γ(ti ) differs from pi , and they are cubic splines because they are obtained by smoothlypiecing together segments of cubic polynomials on M , in the sense of Noakes et al. [NHP89]. Itis also shown in [MS06, Prop. 4.5] that, as the smoothing parameters λ goes to , the optimalcurve converges to the best least-squares geodesic fit to the data points at the given instants oftime. When λ goes to zero, the approximating cubic spline converges to an interpolating cubicspline [MS06, Prop. 4.6].1.2Our approachIn this paper, rather than trying to solve directly the fourth-order differential equation obtainedin [MS06] (a feat that is not attempted in [MS06], except for M Rn ), we propose to searchfor an optimizer of the objective function using a steepest-descent method in an adequate set ofcurves on the Riemannian manifold M . In this section, we present the essence of our approach,and delay the mathematical technicalities until Section 2.We consider the problem of minimizing the objective function of [MSH06], namelyE2 : Γ2 R : γ 7 E2 (γ) Ed (γ) λEs,2 (γ)N λ1X 2d (γ(ti ), pi ) 2 i 02Z01D2 γ D2 γ,dt2 dt2dt,(4)where Γ2 is an adequate set of curves on M to be defined in Section 2. The steepest-descentdirection for E2 is defined with respect to the second-order Palais metricZ 1 2DvD v D2 wDwhhv, wii2,γ hv(0), w(0)iγ(0) dt.(5)(0),(0), dtdtdt2 dt2 γ(t)0γ(0)As we shall see in Section 4, this choice of metric ensures that the gradient of E2 at γ, representedby a vector field G along γ, admits a simple expression. This simple expression makes it possible3
to implement a steepest-descent algorithm on Γ2 , where the next iterate is obtained from thecurrent iterate γ using a line-search procedure along the path ǫ 7 γ ǫ on Γ2 defined byγ ǫ (t) expγ(t) ( ǫG(t));see Section 5. We use an Armijo backtracking procedure, but other stepsize selection methodswould be suitable.We also present a gradient-descent approach for the objective function of [MSH06], namelyE1 : Γ1 R : γ 7 E1 (γ) Ed (γ) λEs,1 (γ)Nλ1X 2d (γ(ti ), pi ) 2 i 02Z1hγ̇, γ̇i dt,(6)0where Γ1 is another adequate set of curves on M defined below. For E1 , the steepest-descentdirection is considered with respect to the first-order Palais metricZ 1Dv Dwhhv, wii1,γ hv(0), w(0)iγ(0) dt.(7),dt dt γ(t)0This choice confers a simple expression to the gradient; see Section 3.Observe that the parameter λ makes it possible to balance between the two conflicting goalsmentioned above: when λ is large, a higher emphasis is on the regularity condition relative to thefitting condition, whereas when λ is small, the fitting condition dominates.The rest of the paper is organized as follows. Section 2 deals with the choice of the curve spacesΓ1 and Γ2 . An expression for the gradient of E1 , resp. E2 , is given in Section 3, resp. 4. Thesteepest-descent method is presented in Section 5. Numerical illustrations are given in Section 6for M R2 and M S2 . Section 7 contains final remarks.2PreliminariesIn this section, we exploit results of Palais [Pal63, §13] and Tromba [Tro77, §6] to define Γ insuch a way that the gradient of E with respect to the Palais metric is guaranteed to exist and beunique.2.1First-order caseWe first consider the objective function E1 defined in (6). Let I denote the unit interval [0, 1] andlet H0 (I, Rn ) denote the set of square integrable functions from I to Rn . The set H0 (I, Rn ) is aHilbert space under pointwise operations and with the inner product hh·, ·ii0 defined byhhv, wii0 Z1hv(t), w(t)i dt,0where h·, ·i is the standard inner product in Rn . Let H1 (I, Rn ) denote the set of absolutelycontinuous maps γ : I Rn such that γ̇ H0 (I, Rn ). Note that absolute continuity is equivalentto requiring that γ̇(t) exists for almost all t I, that γ̇ is summable, and thatZ tγ̇(s) ds.γ(t) γ(0) 0nThen H1 (I, R ) is a Hilbert space under the inner product hh·, ·ii1 defined byhhv, wii1 hv(0), w(0)i hhv̇, ẇii0 .(8)This inner product belongs to a class of Riemannian structures proposed by Linnér [Lin03, §3].4
Let M be a closed C k 4 -submanifold of Rn (k 1). Define H1 (I, M ) to be the set of allγ H1 (I, Rn ) such that γ(I) M . Then H1 (I, M ) is a closed C k -submanifold of the Hilbertspace H1 (I, Rn ). We setΓ1 H1 (I, M ),(9)which ensures that E1 (6) is a well defined C k map, provided that, for all i, pi is in the image ofthe domain of injectivity of the exponential mapping at γ(ti ) (see Lazard and Tits [LT66] for thecase where the manifold is a Lie group).The tangent space to H1 (I, M ) at a curve γ H1 (I, M ) is given byTγ H1 (I, M ) {v H1 (I, T M ) : v(t) Tγ(t) M for all t I},where T M denotes the tangent bundle of M . Moreover, H1 (I, M ) is a complete C k -Riemannianmanifold in the Riemannian structure induced on it as a closed C k -submanifold of H1 (I, Rn ).Note that the induced Riemannian structure on H1 (I, M ) induced by (8) is the “extrinsic”structure given byhv(0), w(0)i hhv̇, ẇii0 ,where v̇ and ẇ are the derivatives in the sense of the embedding space Rn . It thus differs from the“intrinsic” first-order Palais metric defined in (7). However, the extrinsic and intrinsic Riemannianstructures are equivalent on bounded sets [Tro77, Prop. 6.1].From this, it follows that, given γ H1 (I, M ), the tangent space Tγ H1 (I, M ) endowed withthe inner product (7) is a Hilbert space. The gradient of E1 at γ is defined to be the uniqueG Tγ H1 (I, M ) that satisfies, for all w Tγ H1 (I, M ),hhG, wii1,γ DE1 (γ)[w],where DE1 (γ)[w] denotes the derivative of E1 at γ along w. The existence and uniqueness ofG are guaranteed by the Riesz representation theorem. We will use the notation E(γ) for thegradient of a function E at γ, or simply G when E and γ are clear from the context.2.2Second-order caseWe now turn to the objective function E2 defined in (4). Let H2 (I, Rn ) be the set of mapsγ : I Rn with γ H1 (I, Rn ) and γ̇ H1 (I, Rn ). Then H2 (I, Rn ) is a vector space underpointwise operations, and the mapΦ : Rn Rn H0 (I, Rn ) H2 (I, Rn ) : (γ0 , γ̇0 , h) 7 γ,defined by γ(0) γ0 , γ̇(0) γ̇0 , γ̈(t) h(t) for all t I, is an isomorphism. In H2 (I, Rn ),consider the inner product hh·, ·ii defined byZ 1hv̈(t), ẅ(t)i dt.hhv, wii hv(0), w(0)i hv̇(0), ẇ(0)i 0nThen Φ is an isometry and H2 (I, R ) is a Hilbert space.Let M be a closed C k 4 -submanifold of Rn (k 1). Define H2 (I, M ) to be the set of allγ H2 (I, Rn ) such that γ(I) M . Then, by restricting the proof of [Pal63, Th. 6.6] to H2 , oneobtains that H2 (I, M ) is a closed C k -submanifold of the Hilbert space H2 (I, Rn ). We setΓ2 H2 (I, M ),(10)which ensures that E2 is well defined. The tangent space to H2 (I, M ) at a curve γ H2 (I, M ) isgiven byTγ H2 (I, M ) {v H2 (I, T M ) : v(t) Tγ(t) M for all t I}.Given γ H2 (I, M ), consider the mappingΦ : Tγ(0) M Tγ(0) M H0 (I, Tγ(0) M ) Tγ H2 (I, M )5
that maps (v0 , v̇0 , g) to the vector field v along γ defined byv(0) v0 ,Dv(0) v̇0 ,dtD2 v(t) Pγt 0 g(t),dt2where Pγt 0 is the parallel transport along γ. Recall that the parallel transport is an isometry.The map Φ is an isomorphism of vector spaces between its domain and image, and it is an isometrywith the obvious metric on the domain and the second-order Palais metric (5) on the image. Sincethe domain of Φ is a Hilbert space, its image is also a Hilbert space endowed with the innerproduct (5). Hence the Riesz representation theorem applies.3Gradient of E1 in the first-order Palais metricWe derive an expression for the gradient of E1 Ed λEs,1 (6) over Γ1 (9) endowed with thefirst-order Palais metric (7). The gradient evaluated at a curve γ involves the operations of paralleltransport and covariant integral along γ.3.1Derivative of EdWe first give an expression for the derivative of the ith term in Ed , namely,fi : Γ1 R : γ 7 1 2d (γ(ti ), pi ).2Let expp denote the Riemannian exponential map at p M ; see, e.g., [Boo75, dC92]. SinceM is a closed Riemannian submanifold of Rn , it follows that M is complete (see [Pal63, p. 326]),which means that expp ξ exists for all ξ Tp M . If q M is not in the cut locus of p, then thereexists a unique minimizing geodesic αpq with αpq (0) p and αpq (1) q (see [dC92, corollary13.2.8]), and we define exp 1p (q) α̇pq (0). Note that in this case, it also holds that p is not in thecut locus of q (see [dC92, corollary 13.2.7]), and we have exp 1q (p) α̇pq (1). An expression forthe derivative of fi is readily obtained from the following result.Theorem 3.1 (Karcher, 1977). Let M be a complete Riemannian manifold, let p be a point ofM and let q be a point of M that is not in the cut locus of p. Then the squared distance functionto p is differentiable at q and we have, for all ξ Tq M ,1 2Dd (p, ·)(q)[ξ] ξ, exp 1q p .2Proof. This proof is essentially a restriction of the proof of [Kar77, Th. 1.2]. Let α be defined byα(t) expq (tξ). Consider the family of geodesics from p to α(t): cp (s, t) expp (s exp 1p α(t)).Since the cut locus is closed [dC92, corollary 13.2.10], this expression is well defined for all t in addneighborhood of 0 and all s [0, 1]. Denote c′p dscp (s, t) and ċp dtcp (s, t). We know that′d(p, α(t)) kcp (s, t)k is independent of s. We have successively1 d ′1 d 2d (p, α(t)) c (s, t), c′p (s, t)2 dt2 dt pwhich does not depend on s,D ′cp (s, t), c′p (s, t)dtD ċp (s, t), c′p (s, t)ds 6
which still does not depend on s, thus1 Z1 Zdċp (s, t), c′p (s, t) dsds00sinceD ′ds cp (s, t)D′ċp (s, t), cp (s, t) dsds 0 (geodesic property), ċp (1, t), c′p (1, t)since ċp (0, t) 0,DE α̇(t), exp 1p.α(t)Since 12 Dd2 (p, ·)(q)[ξ] 1 d 22 dt d (p, α(t)) t 0 ,the result follows.In view of this result, we have that the derivative of fi at γ along w Tγ (Γ1 ) isDfi (γ)[w] hw(ti ), vi i ,wherevi expγ(ti ) (pi ),provided that γ(ti ) is not in the cut locus of pi . This is a mild condition, since the cut locus hasmeasure zero [GHL04, lemma 3.96]. Finally, the derivative of Ed is given byDEd (γ)[w] NXhw(ti ), vi i .i 03.2Gradient of EdThe gradient of fi at γ, with respect to the first-order Palais metric (7), is the unique element giof Tγ Γ1 such that, for all w Tγ Γ1 ,hhgi , wii1 Dfi (γ)[w].The next theorem gives an expression for gi .Theorem 3.2. The gradient of the function fi : Γ1 R : γ 7 d2 (γ(ti ), pi ) evaluated at γ Γ1is the vector field gi along γ defined by (1 t)ṽi (t),0 t tigi (t) ,(1 ti )ṽi (t),ti t 1where vi exp 1γ(ti ) (pi ) Tγ(ti ) M and ṽi is the parallel transport of vi along γ.Proof: See Appendix A.1.1.Observe that gi is covariantly linear from 0 to ti , and is covariantly constant from ti to 1. Inother words, the covariant derivative of gi is covariantly constant (ṽi ) until ti , and it is 0 afterthat. Note also that ṽi (ti ) vi .Once we have the gradient for each of the terms in Ed , the gradient of Ed , under the first-orderPalais metric, is simply their sumNXgi .(11)G1 i 07
3.3Derivative of Es,1The derivative and gradient of Es,1 (2) can be readily deduced, e.g., from [Tro77, §6] or [KS06,Th. 1]. We give a full development here for convenience.Recall thatZ1 1hγ̇(t), γ̇(t)i dt.Es,1 (γ) 2 0Define a variation of γ to be a smooth function h : [0, 1] ( ǫ, ǫ) M such that h(t, 0) γ(t)for all t [0, 1]. The variational vector field corresponding to h is given by w(t) hs (t, 0) wheres denotes the second argument in h. Thinking of h as a path of curves in M , we define F (s) asthe energy of the curve obtained by restricting h to [0, 1] {s}. That is,F (s) 12Z1hht (t, s), ht (t, s)i dt .0We now compute,Z 1Z 1Z 1DhsDwDht′(t, 0), ht (t, 0) dt (t, 0), ht (t, 0) dt (t), γ̇(t) dt,F (0) dsdtdt000since ht (t, 0) is simply γ̇(t). Hence the derivative of Es,1 at γ along w is given byDEs,1 (γ)[w] Z03.41Dw(t), γ̇(t) dt.dtGradient of Es,1In view of the above expression for the derivative of Es,1 , the following result directly follows fromSection A.1.2.Theorem 3.3. The vector field H1 along γ that provides the gradient of the function Es,1 withrespect to the first-order Palais metric satisfies the equation:DH1(t) γ̇(t), H1 (0) 0.dt(12)In the case M Rn , the gradient vector field is simply H1 (t) γ(t) γ(0).3.5Gradient of E1Since E1 Ed λEs,1 , the gradient of E1 follows directly from the gradients of Ed and Es,1computed above. We thus have that E1 G1 λH1 , with G1 given (11) and H1 given by (12).4Gradient of E2 in the second-order Palais metricRecall that E2 Ed λEs,2 is defined on Γ2 (10) byNE2 (γ) λ1X 2d (γ(ti ), pi ) 2 i 02Z01D2 γ D2 γ,dt2 dt2dt.(13)The purpose of this section is to obtain an expression for the gradient of E2 with respect to thesecond-order Palais metric (5).8
4.1Gradient of EdThe derivative does not depend on the metric, in contrast to the gradient. Thus we have, as inSection 3,Dfi (γ)[w] hw(ti ), vi i ,where fi denotes the function γ 21 d2 (γ(ti ), pi ) and vi exp 1γ(ti ) (pi ).Theorem 4.1. The gradient of the function fi : Γ2 R : γ d2 (pi , γ(ti )) at γ Γ2 with respectto the second-order Palais metric (5) is given by the vector field gi along γ defined by (1 ti t 21 ti t2 61 t3 )ṽi (t) 0 t tigi (t) (1 tti 12 tt2i 16 t3i )ṽi (t) ti t 1,where ṽi is the parallel transport of vi along γ.Proof: See Appendix A.2.1.This gradient function is a cubic Ppolynomial before ti and is a linear polynomial after ti . TheNtotal gradient is given by G2 (t) i 0 gi (t). Another way of writing this summation is: forti 1 t ti , we getG2 (t) 4.2Ni 1XX1111(1 tj t tj t2 t3 )ṽj (t).(1 ttj tt2j t3j )ṽj (t) 2626j ij 0(14)Derivative of Es,2Let γ(s, t) be a collection of curves indexed by s; for a fixed s we have a curve parameterized byt. For s 0 that curve is simply called γ(t). Define w γ(s,t) s s 0 as the tangent vector at γ.dThen DEs,2 (γ)[w] dsF (s) s 0 , where1F (s) 2Z01D γ D γ( ),) dt.dt t dt tTaking the derivative with respect to s:Z 1dD D γD γF (s) ( ( )), ( ) dtdsds dt tdt t0Z 1 γ γD D γD γ[R(w, )( ) ( ( ))], ( ) dt, t tdt ds tdt t0where R is the Riemannian curvature tensor defined as:R(D DD D γ γ,)(v) (v) (v). s tds dtdt ds(Note that the curvature tensor is sometimes defined with the opposite sign in the literature.)D γD γ( t ) dt( s ), the desired derivative at s 0 becomes:Since ds1D2D[R(w, γ̇)(γ̇) 2 (w)], (γ̇) dtdtdt0Z 1Z 1 2DDDR(w, γ̇)(γ̇), (γ̇) dt (w), (γ̇) dt.dtdt2dt00dF (s) s 0 dsZThis is the sought expression for DEs,2 (γ)[w].9(15)
4.3Gradient of Es,2We will analyze the two terms in (15) separately.The Riemannian curvature tensor has certain symmetries: for vector fields a, b, c, d along γ,hR(a, b)(c), di hR(b, a)(c), di hR(a, b)(d), ci hR(c, d)(a), bi ,which allows us to rewrite the first term of (15) asZ 1Z 1D2 γhA(t), w(t)i dt .R( 2 (t), γ̇(t))(γ̇(t)), w(t) dt dt00Note that this equation defines a vector field A along the curve γ. We need a vector field H2 withthe property that hhH2 , wii2 hA, wi. In view of Appendix A.2.2, the solution is given by11H2 (t) Ĥ(t) [ S̃(t) t(Q̃(t) S̃(t)) t2 (Q̃(t) S̃(t)) t3 S̃(t)],26where Ĥ is the four times covariant integral of A (so that it satisfiesconditionsalong γ of2D3 ĤĤ(0) DdtĤ (0) DdtĤ2 (0) dt3 (0)2D3 ĤQ DdtĤ2 (1) and of S dt3 (1).D4 Ĥdt4 (t)(16) A(t)) with initial 0, and where Q̃ and S̃ are the parallel transportER 1 D D2DWe now consider the second term in (15), that is, 0 dtdt. In view of Sec2 (w), dt (γ̇)tion A.2.3, this term can be written as hhH3 , wii2 , where H3 satisfiesD2 γD 2 H3 ,2dtdt2H3 (0) DH3(0) 0,dt(17)23that is, H3 is two times covariant integral of Ddt2γ with initial conditions H3 (0) DHdt (0) 0.nIn case M R , the two terms are simply H2 (t) 0 and H3 (t) γ(t) γ̇(0)t γ(0) for allt I.4.4Gradient of E2Combining the two gradient terms, we get the gradient of E2 under the second-order Palais metric: E2 G2 λ(H2 H3 ),where G2 is given in (14), H2 in (16), and H3 in (17).5Steepest-descent algorithm on the curve spacesLet E stand for E1 (6), resp. E2 (4), Γ for the set Γ1 (9), resp. Γ2 (10), of curves on the Riemannianmanifold M , and let Γ be endowed with the first-order Palais metric (7), resp. second-order Palaismetric (5). We propose the steepest-descent method for E described in Algorithm 1.The algorithm creates a sequence of curves (γk )k 0,1,. Γ with decreasing energy E(γk ). Theinitialization step consists in choosing an arbitrary curve in Γ to be the starting curve γ0 . Then,given the current iterate γk , the algorithm computes the gradient E(γk ) and updates the curveto γk 1 according toγk 1 (t) expγk (t) ( ρ̂k E(γk )(t)), t I,where ρ̂k is a step size chosen using some step size selection rule (see, e.g., [Ber95]). We have chosena modified version of Armijo backtracking procedure by imposing strong Wolfe conditions [Wol69];see Algorithm 2. The algorithm is stopped when a certain pre-determined stopping criterion issatisfied. The criterion can be a threshold on the norm of E(γk ), for example.Whereas analyzing the convergence of steepest-descent type methods on finite-dimensionalmanifolds is relatively simple (see [AG09]), the convergence analysis of steepest-descent methods10
Algorithm 1 Gradient descent1: Given a scalar ǫ ]0, 1[ and an initial curve γ0 , arbitrary element of Γ;2: k : 0;3: repeat4:k : k 1;5:Compute E(γk ) and E(γk );6:Find the step size ρ̂k using algorithm 2;7:Set γk (t) expγk 1 (t) ( ρ̂k E(γk )(t));8: until k E(γk )k ǫ9: return γ̂ : γkAlgorithm 2 Step size selection1: Given scalars ρ0 ]0, 1[, ǫ 0 very small, 0 σ1 σ2 1, a function f and a descentdirection q of f at x;2: set k 0 and set βk ρ0 ;3: until (βk ǫ) or (f (x βk q) f (x) σ1 βk hh f (x), qii and hh f (x βk q), qii σ2 hh f (x), qii ) do4:k : k 1;5:βk βk 1 ρ0 ;6: end7: return ρ̂ : βkon infinite-dimensional spaces is no trivial matter; see [SZ04] and references therein. Analyzingthe convergence of Algorithm 1 is the object of ongoing research. Nevertheless, it is reasonable toexpect that the algorithm behaves like steepest-descent methods in finite dimension: the sequenceof iterates γk has a single limit (see [AMA05]) which, unless the initial curve is maliciously chosen,is a local minimizer of the objective function E. These expectations are corroborated by ournumerical experiments; see Section 6.6Illustration on some specific manifolds: M R2 , S2In this section we present some illustrations of our gradient descent approach to finding optimalcurves. In the case of Euclidean spaces, it is sometimes possible to derive expressions for theoptimal curves under E1 and E2 directly. In those situations, we can compare our numericalsolutions to the analytical expressions, and characterize the performances. In the remaining cases,where the analytical solutions are not readily available, we will simply illustrate the results obtainedusing our procedures. Examples involving the analytical expressions will have M Rn and whilethe other cases will have M S2 .6.1Analytical solution of E1 in R2As the first example we will consider the problem of finding the optimal curves under E1 whenM R2 . For simplicity, we will take λ 1 in (6). This case is simple enough to seek an analyticalexpression as follows. Let N 2 and the three data points be given by p0 ( A, 0), p1 (0, B), p2 (A, 0), at the time instants t0 0, t1 0.5, t2 1, respectively; here A, and B betwo real variables. Using the symmetry of the given points, we will note that q0 ( a, c), q1 (0, b), q2 (a, c) will be the control points of an intermediate curve given by the gradient descentmethod. Our goal is to find the values of variables a, b, and c such that the piecewise geodesiccurve connecting q0 , q1 , q2 is a minimum of E1 . By computing Ed and Es,1 manually we getE1 2(A a)2 2c2 (B b)2 4(a2 (b c)2 ). The critical points are given by the equation E1 E11 E1 0, i. e. in terms of partial derivatives we have E a b c 0. This system has11
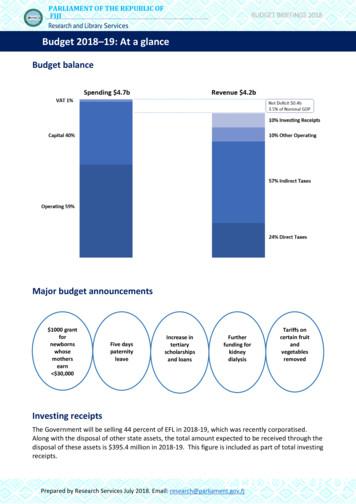
4510.0254000.020.5350.0150 4 3 2 101The original parametrized curve234 0.5 6 4 202The original parametrized 0406080100(c)120140160180(d)Figure 1: (a) and (b): The minimum of E1 in M R2 reached by the gradient descent method withrespect to Palais metric using different starting curves for λ 1, (c): the step length variation, and (d):the energy evolution versus iterations for the example shown in (a).3132.50.92.520.821.50.71 λ 11.50.510.6 λ 0.10 λ 10.5 0.50.50.4 10 4 3 2 101234 1.5 4 3 2 10(a)12340.20.30.40.5(b)0.60.70.50.911.2 λ 10.80.81.40.70.90.7(c)0.810.61 λ 50.60.40.50.30.40.20.80.6 λ .80.91(f)Figure 2: The minimum of E1 in M R2 reached by the gradient descent method with respect tofirst-order Palais metric using different values of λ.only one solution given by a 31 A, b 37 B, and c 72 B, and the minimum of E1 is given by thepiecewise geodesic curve connecting points q1 ( A/3, c), q2 (0, 3B/7), and q3 (A/3, 2B/7).Shown in Figures 1((a) and (b)) are two optimal curves under E1 obtained by our algorithm,for two different initial conditions. In each case, the green curve shows the initial condition and theblack curve shows the final result obtained numerically. The red curves show the optimal obtainedusing the analytical solution. The coincidence of black and read curves shows the accuracy and thestability of our algorithm. In Figures 1((c) and (d)) we show the variation of the
A Gradient-Descent Method for Curve Fitting on . as the curve that minimizes the weighted sum of a sum-of-squares term penalizing the lack of . curve converges to the best least-squares geodesic fit to the data points at the given instants of time. When λ goes to zero, the approximating cubic spline converges to an interpolating cubic .
Method of Gradient Descent The gradient points directly uphill, and the negative gradient points directly downhill Thus we can decrease f by moving in the direction of the negative gradient This is known as the method of steepest descent or gradient descent Steepest descent proposes a new point
2 f( ). While any method capable of minimizing this objective function can be applied, the standard approach for differentiable functions is some form of gradient descent, resulting in a sequence of updates t 1 t trf( t). The performance of vanilla gradient descent, however, is hampered by the fact that it only makes use
16.2.1 The Basic Gradient Descent Method Gradient descent is an iterative algorithm to approximate the opti-mal solution x. The main idea is simple: since the gradient tells us the direction of steepest increase, we’d like to move opposite to the
5.4.2 Steepest descent It is a close cousin to gradient descent and just change the choice of norm. Let’s suppose q;rare complementary: 1 q 1 r 1. Steepest descent just update x x t x, where x kuk r u u argmin kvk q 1 rf(x)T v If q 2, then x r f(x), which is exactly gradient descent.
Bruksanvisning för bilstereo . Bruksanvisning for bilstereo . Instrukcja obsługi samochodowego odtwarzacza stereo . Operating Instructions for Car Stereo . 610-104 . SV . Bruksanvisning i original
A Gradient Descent Implementation of Adaptive Pulse Compression Patrick M. McCormick1, Shannon D. Blunt1, and Thomas Higgins2 1Radar Systems Lab, University of Kansas, Lawrence, KS 2Radar Division, Naval Research Laboratory, Washington, DC Abstract—Gradient descent is an iterative method of determining the minima or maxima of a function.
Steps in Gradient Method Development 1. Run a wide gradient (e.g., 5 to 100% B) over 40-60 min. From this run, decide whether gradient or isocratic elution is best 2. If gradient elution is chosen, eliminate portions of the gradient prior to the first peak and following the last peak. Use the same gradient
Mirror descent 5-2 Convex and Lipschitz problems minimizex f (x) subject to x ! C f is convex andLf-Lipschitz continuous Mirror descent 5-35 Outline Mirror descent Bregman divergence Alternative forms of mirror descent Convergence analysis f (xt) !! f (xt),x " xt " " 1 2!t #x " xt#2