CIE IGCSE MATHS 0580 - PapaCambridge
TIONSON THESYLLABUS
TABLE OF CONTENTS2CHAPTER 15CHAPTER 211CHAPTER 316CHAPTER 418CHAPTER 520CHAPTER 622CHAPTER 723CHAPTER 8NumbersAlgebra and GraphsGeometryMensuration (Perimeters, Areas and Volumes)TrigonometryMatrices and TransformationsProbabilityStatistics
CIE IGCSE MATHEMATICS//05801.3 Square and Cube Numbers1. NUMBERSQuestion 3:1.1 Integers, HCF/LCM, Prime numbers, SigFigs, Dec PlacesQuestion 1:Find the lowest common multiple (LCM) of 36 and 48.[2]Solution:[2]Solution:Apply the power to everything inside the brackets anduse the general rule that (π π₯ )π¦ π π₯π¦33325 π₯ (10 5)1Note that 32 25 hence 325 23 (325 ) π₯ 6 23 π₯ 6 πππ1.4 Conversion - Percentages, Fractions &DecimalsQuestion 4:1.2 Sets and Venn DiagramQuestion 2:Write the recurring decimal 0.32 Μ as a fraction.[0.32 Μ means 0.3222.][2]Solution:[1][1]Solution:Part (a)(i)π(π) is the number of elements in set M. M is all theeven numbers between 2 and 16 inclusive which isπ(π΄) πPart (a)(ii)(π π)β² are the elements not in the union of sets Pand M.(π π) {2, 3, 4, 5, 6, 7, 8, 10, 11, 12, 13, 14, 16}(π· π΄)β² {π, ππ}Part (b)Simplify (32π₯ 10 )1We can do this by writing out all of the multiples ofthe two numbers. The multiples of 36 are:36, 72, 108, 144, 180, The multiples of 48 are48, 96, 144, 192, We can see that the lowest common multiple is:144a) π {x: 2 x 16, x is an integer}M {even numbers}P {prime numbers}i) Find n(M).ii) Write down the set (P M)β². [1]b) On the Venn diagram, shade A Bβ².35We need to get rid of the recurring decimal by doingthe following100 0.32Μ 32. 2Μ10 0.32Μ 3. 2Μ100 0.32Μ 10 0.32Μ 90 0.32Μ 32. 2Μ 3. 2Μ 90 0.32Μ 29Now divide by 90πππ. ππΜ ππ1.5 Order by SizeQuestion 5:Write the following in order of size, smallest first. [2]22Ο3.143.14237Solution:The order of size can be found by writing all of thesenumbers out to the same number of decimal places,and then comparing. In order to do this, put each ofthe values into the same format (decimals) using theβS Dβ button (located above βDELβ) on your calculator.π 3.14159 (5. π. π)3.14 3.14000 (5. π. π)22 3.14286 (5. π. π)73.142 3.14200 (5. π. π)3 3.00000 (5. π. π)Therefore, the order we get (smallest to largest) is:ππ3 3.14 3.142 πPAGE 2 OF 26
CIE IGCSE MATHEMATICS//05801.6 Standard FormSolution:Question 6:2Write 2.8 10 as an ordinary number.[1]Solution:We can write 2.8 x 102 as an ordinary number likethis:2.8 x 102 simply means 2.8 x 100π. π πππ πππ1.7 Addition/Subtraction/Multiplication/Division of Fractions & Decimals1.9 BoundsQuestion 7:Show that13 8216Do not use a calculator and show all the steps of yourworking.[2]1Solution:This question is most simply done by converting1everything to proper fractions. We want to change 1 2into a proper fraction, which can be done as shown.112 131 1 222 22Our problem then becomes3 3 2 16We can use βKeep-Change-Flipβ to change this to a3multiplication problem. We keep , change into ,and flip31616to 3 .Write all numbers correct to one significant figure: 4 309 3Do the calculations.2 30 60 66We get the final answer:ππ23 16 2 3We now can multiply the numerators anddenominators.3 16 48 82 36ππHence π π ππ π.Question 9:An equilateral triangle has sides of length 16.1 cm,correct to the nearest millimetre.Find the lower and upper bounds of the perimeter ofthe triangle.[2]Solution:An equilateraltriangle has all sides16.1ππand angles equal.16.1ππWe know that eachside is 16.1ππ to thenearest mm. This16.1ππmeansthat, each side couldbe between 16.15ππ and16.05ππ.We can therefore calculate:The minimum perimeter/lower bound is:16.05 16.05 16.05 ππ. ππππAnd the maximum perimeter/upper bound is:16.15 16.15 16.15 ππ. ππππ1.10 RatiosQuestion 10:1.8 EstimationQuestion 8:By writing each number correct to 1 significant figure,estimate the value of 3 9 29 38 9 2 7Show all your working.[2]The scale on a map is 1: 20 000.(a) Calculate the actual distance between two pointswhich are 2.7 cm apart on the map.Give your answer in kilometres.[2]2(b) A field has an area of 64 400 π .Calculate the area of the field on the map in ππ2[2]PAGE 3 OF 26
CIE IGCSE MATHEMATICS//0580Solution:Solution:Part (a)By inputting the values into your calculator, you get:Multiply the distance on the map by the scale factor tofind the real distance in centimeters.πππ π‘ππππ 2.7ππ 20 000πππ π‘ππππ 54 000 ππDivide the distance by 100 to get the distance inmeters. (1m 100cm)πππ π‘ππππ 540 πDivide the real distance in meters by 1000 to get thedistance in kilometers (1km 1000m)π πππππππ π.ππ ππ31 (cos(30))2 (sin(30))20.5 344 1 3 32(sin(120)(cos(120))32 222So, the answer is: ππ1.13 TimeQuestion 13:A train leaves Zurich at 22 40 and arrives in Vienna at07 32 the next day. Work out the time taken.[1]Solution:Part (b)Multiply the area by 10 000 to get the area in squarecentimeters.(1m2 100cm x 100cm 10 000 cm2)ππππ 644 000 000 ππ2Divide by the scale factor 20 0002to get the area onthe map. (Note: Area scale factor is the square of thelength scale factor)644 000 000 ππ2ππππ ππ πππ (20 000)2ππππ ππ πππ π. ππ πππ1.11 PercentagesQuestion 11:In 1970 the population of China was 8.2 x 108 .In 2007 the population of China was 1.322 x 109 .Calculate the population in 2007 as a percentage ofthe population in 1970.[2]Solution:The population in 2007 as a percentage of thepopulation in 1970 can be calculated by:ππππ’πππ‘πππ ππ 2007ππππ’πππ‘πππ ππ 1970We can count the time it takes to get us to the Vienna.Add 20 minutes to take it to the next hour:22: 40 20π 23: 00Add 1 hour to take it to the next day (24:00 isequivalent to midnight, or 00:00)23: 00 1βπ 24: 00 ( 00: 00)Now add 7 hours and 32 minutes to get to the desiredtime00: 00 7βπ 32π 07: 32The time taken is all the hours and minutes addedtogether like this20π 1βπ 7βπ 32πTotal time (8hr 52m)1.14 Currency ConversionsQuestion 14:(a) In 2007, a tourist changed 4000 Chinese Yuan intopounds ( ) when the exchange rate was 1 15.2978 Chinese Yuan. Calculate the amount hereceived, giving your answer correct to 2 decimalplaces.[2](b) In 2006, the exchange rate was 1 15.9128Chinese Yuan. Calculate the percentage decreasein the number of Chinese Yuan for each 1 from2006 to 2007.[2] 100,Substituting in the values gives:1.322 109 100 161. 2Μ1951Μ8.2 108The answer after rounding is:πππ%Part (a)1.12 Using a calculatorQuestion 12:Use your calculator to find the value of(cos30 )2 (sin 30 )22(sin120 )(cos 120 )Solution:In order to change from Chinese Yuan into pounds, wecan do this:1 πΆβππππ π ππ’ππ 0.065374000 πΆβππππ π ππ’ππ 0.06537 40004000 πΆβππππ π ππ’ππ 261.4755But we need this to the nearest pennyππππ πͺππππππ ππππ πππ. π[2]PAGE 4 OF 26
CIE IGCSE MATHEMATICS//0580Part (b)To calculate the percentage decrease we need to dothe following:πβππππ ππ ππππ’ππ‘ ππ πβππππ π π¦π’ππ πππ πππβ 1ππππ’ππ‘ ππ πβππππ π π¦π’ππ πππ πππβ 1 ππ 2006 10015.9128 15.2978 100 3.864815.9128Hence the percentage decrease is 3.865%1.15 Finance ProblemsQuestion 15:Emily invests x at a rate of 3% per year simpleinterest. After 5 years she has 20.10 interest. Findthe value of x.[3]Solution:The equation for simple interest isπ π₯ π π₯ (1 π‘)100Where: π₯ Principal investment value i Interest gained R Interest rate (%) t Investment time3 5π₯ 20.1 π₯ (1 )10020.11 1 0.06π₯20.1π₯ 0.06π πππ1.16 Finance ProblemsQuestion 16:Zainab borrows 198 from a bank to pay for a newbed. The bank charges compound interest at 1.9 % permonth. Calculate how much interest she owes at theend of 3 months. Give your answer correct to 2decimal places.[3]Solution:To calculate how much interest she owes on 198 atthe end of the 3 months we first must calculate thetotal amount after interest at the end of the 3 months.This is done as follows:π 3198 (1 )100where π is the interest rate. As we know that theinterest rate is 1.9%,1.9r (1 100) 3 1.019and hence the total amount after interest is:198 1.0193 209.50.Hence Zainab owes the bank 209.5 198 11.5So, the answer is: ππ. πFOR MORE PAST PAPER QUESTIONS, VISITWWW.SAVEMYEXAMS.CO.UK2. ALGEBRA AND GRAPHS2.1 Using Algebra to Solve ProblemsQuestion 17:Simplify 16 4(3π₯ 2)2 .[3]Solution:Simplifying the equation gives:16 4(3π₯ 2)2 16 4(9π₯ 2 12π₯ 4) 16 36π₯ 2 48π₯ 16 36π₯ 2 48π₯ 12π₯(4 3π₯)So, the answer is:πππ(π ππ)PAGE 5 OF 26
CIE IGCSE MATHEMATICS//05802.2 Factorisation (Linear)2.5 Linear equationsQuestion 18:Factorise completely.a) 2π 4 ππ 2π[2]b) 162 β 8π‘ 2[2]Solution:Part (a)(π π)(π π)We can check this by expanding it back out:ππ 2π 2π 4Part (b)We can start off by factorising out the common factorof 22(81 4π‘ 2 )Then we can see that this is the difference of twosquares 2(92 (2π‘)2 ) π(π ππ)(π ππ)2.3 Algebraic fractionsQuestion 21:Solve the equation.5 β 2π₯ 3π₯ β 19Solution:5 2π₯ 3π₯ 19Add 2x to both sides of the equality:5 5π₯ 19Add 19 to both sides:5π₯ 24Divide both sides by 5:24π₯ 5π π. π2.6 Simultaneous Linear EquationsQuestion 22:Solve the simultaneous equations.0.4π₯ β 5π¦ 272π₯ 0.2π¦ 9Question 19:[3]Solution:π‘ 1Multiply 3 by π‘ 1 to create a common denominator:3(π‘ 1) π‘ 2 π‘ 1π‘ 1Combine the fractions:3π‘ 3 (π‘ 2) π‘ 13π‘ 3 π‘ 2 π‘ 1ππ ππ πRearrange one of the equations to get just x or just y onone side:0.4π₯ 27 5π¦Substitute this into the second equation:5(27 5π¦) 0.2π¦ 9Simplify:135 25.2π¦ 9Solve:25.2π¦ 126π πSubstitute your answer into one of the equations:2π₯ 1 9Solve for x:2π₯ 10π πSo the answer is:π π, π π2.4 IndicesQuestion 20:Simplify [3]Solution:Write as a single fraction in its simplest form.π‘ 23 π‘ 15 3π₯28[2]1 5π₯ 22[2]Solution:To simplify the equation, we use the fact thatπ₯ π π₯ π π₯ π πHence:5 3 1 55 1 3 55π₯ 2 π₯ 2 ( ) π₯ 2 2 π₯ 4828 24So, the answer is:ππ. ππ ππ π π ππPAGE 6 OF 26
CIE IGCSE MATHEMATICS//05802.7 Linear inequalities2.8 Graphical inequalitiesQuestion 23:Solve the inequality.3x 1 11x 2Question 25:[2]Solution:To solve the inequality 3π₯ 1 11π₯ 2 we mustrearrange for π₯.3π₯ 1 11π₯ 2 3π₯ from both sides 1 8π₯ 2 2 from both sides 3 8π₯Divide both sides by 83 π₯8Hence we getππ πFind four inequalities that define the region, R, on thegrid.[4]2.7 Quadratic EquationsSolution:Question 24:π¦ π₯ 2 7π₯ β 5 can be written in the formπ¦ (π₯ π)2 π.Find the value of a and the value of b.[3]Solution:If we expand (π₯ π)2 and collect terms we getπ¦ (π₯ π)2 π π₯ 2 2ππ₯ π2 πIf we now compare coefficients of the powers of x wehaveπΆπΉ π₯ 1 : 2π 7π π π or 3.5πΆπΉ π₯ 0 (π’πππ‘π ): π2 π 549 π 5420 49 π 44πππ π or -17.25The lines on the grid that border R areπ¦ 4π¦ 3π₯ 2π¦ π₯R is above 3 and below 4, to the right of 2 and to theleft of the diagonal line. Note that solid lines mean weinclude them in the inequality. This is written asπ ππ ππ ππ π2.9 Sequences and nth termQuestion 26:Find the nth term of each of these sequences.(a) 16, 19, 22, 25, 28, .(b) 1, 3, 9, 27, 81, .[2][2]Solution:Part (a)The difference between the terms is 3. The sequencecan then be written as3π πWhere a is some real number and n is the term. Thefirst term is then3 π 16 π 13Henceπππ ππππ ππ ππPAGE 7 OF 26
CIE IGCSE MATHEMATICS//0580Part (b)Each term is a power of 3 so our sequence has the form3 π(π)If we substitute in some values, we can see that1 3 π(1) π(1) 03 3 π(2) π(2) 1Henceπ(π) π 1Final answerπππ ππππ ππ π2.10 Direct/Inverse proportionalityQuestion 27:t varies inversely as the square root of u.t 3 when u 4.Find t when u 49.[3]Solution:We are told that π‘ varies inversely with the square rootof π’. Written mathematically, this says:1π‘ π’By adding a constant of multiplication we can make thisa proper equation:ππ‘ π’We are given values for t and u, so we can rearrangeand solve for k.ππ‘ π’multiply both sides by uπ‘ π’ πPlugging in values3 4 π 3(2) 6π 6Hence our equation becomes6π‘ π’We are asked to find π‘ when π’ 49.πππ ππ π2.11 Kinematics, Distance-Time & SpeedTime GraphsQuestion 28:A car of length 4.3 m is travelling at 105 km/h.It passes over a bridge of length 36m.Calculate the time, in seconds, it takes to pass over thebridge completely.[3]Solution:The car is on the bridge when its front is on the bridgeand exits when its rear leaves. The total distance totravel is therefore36 4.3 40.3πConverting the speed into m/s, first we multiply by1000 to get the units in m/hrπππππ 105 ππβ 1 1000πππππ 105000πβ 1Next, we have to turn it into m/sπππππ 105000πβ 1 (602 )105000πππππ ππ 13600175πππππ ππ 16Using the speed distance time οΏ½οΏ½ππ π‘πππ17540.3π 1ππ 6π‘πππRearrange for time6π‘πππ 40.3 175 π. ππ π (ππ π)PAGE 8 OF 26
CIE IGCSE MATHEMATICS//05802.11 Constructing Graphs & SolvingEquations GraphicallyPart (c)Question 29:1,π₯ 02π₯ 2(a) Complete the table of values.π(π₯) π₯ [2](b) On the grid, draw the graph of π¦ π(π₯) for β3 x β0.3 and 0.3 x 2.[1](c) Use your graph to solve the equation π(π₯) 1 [1](d) There is only one negative integer value, k, forwhich f(x) k has only one solution for all real x.Write down this value of k.[1]1(e) The equation 2π₯ 2π₯2 2 0 can be solved usingthe graph of y f(x) and a straight line graph.i.Find the equation of this straight line [1]ii.On the grid, draw this straight line and solve1the equation 2π₯ 2 2 0.[3]2π₯Solution:Part (a)We use calculator to find the values of π(π₯) for x -1and x 1.π( π) π. π,π(π) π. πPart (b)We plot the line y 1 and find the x-coordinate ofthe point of intersection.From the graph, we can see that the x-coordinate of thepoint isπ π. πPart (d)From the graph, we can clearly see that π π,since for -2 and any other negative integer, thereare two solutions to f(x) k.π πPart (e)(i)Subtract (x-2) from both sides of the equation.1π₯ 2 2 π₯2π₯We can see that the right side of the equation is ouroriginal function.Therefore, the left-hand side must be the straight linewe are looking for.π π πPart (e)(ii)We plot a line π¦ 2 π₯ and find the x-coordinate ofthe point of intersection with the original graph to solve12π₯ 2π₯2 2 0From the graph, we can see that the x-coordinate of thepoint, and hence the solution to the equation12π₯ 2π₯2 2 0 isπ π. ππPAGE 9 OF 26
CIE IGCSE MATHEMATICS//05802.11 Tangents & Gradients2.12 FunctionsQuestion 30:Question 31:4x 3f(x) 5x 7g(x) ,x 3(a) Findi.fg(1)ii.gf(1)iii.g-1(x)iv.ff-1(2)(b) f(x) g(x)i.Show that 5π₯ 2 8π₯ 25 0ii.Solve 5π₯ 2 8π₯ 25 0. Show all yourworking and give your answers correct to 2decimal places.Part (a)(i)(a) Work out the gradient of the line L[2](b) Write down the equation of the line parallel to theline L that passes through the point (0, 6).[2]Solution:Part (a)Gradient found by usingπ¦2 π¦1π₯2 π₯1Choose the points (1, 1) and (0, -1)1 ( 1)π 1 0 ππ Part (b)Parallel means the same gradient, so 2. This gives usthe equationπ¦ 2π₯ πc is the y intercept which is given as 6π ππ π[2][2][2][2][3][4]Solution:We apply f(x) to g(x) like soππ(π₯) 5π(π₯) 720 7π₯ 320ππ(1) 71 3 10 7 πPart (a)(ii)We apply the function g to the output of function fgiving:4ππ(π₯) π(π₯) 34 5π₯ 7 3π ππ πPart (a)(iii)Let π¦ π(π₯). If we rearrange for π₯ π(π¦) then thatfunction of y will be π 1 (π¦).4π¦ π₯ 3Multiply both sides by π₯ 3π¦(π₯ 3) 4Divide both sides by y4π₯ 3 π¦Add 3 to both sides4π₯ 3 π 1 (π¦)π¦π π π (π) ππPAGE 10 OF 26
CIE IGCSE MATHEMATICS//0580Part (a)(iv)3. GEOMETRYInverse function applied to the function reverses itseffect, soπ π π(π) π3.1 Properties of ShapesQuestion 32:Part (b)(i)ZEBRAWe have5π₯ 7 4π₯ 3Multiply both sides by π₯ 3(5π₯ 7)(π₯ 3) 4Expand5π₯ 2 7π₯ 15π₯ 21 4Rearrange and simplify forming a quadratic equationthat equals zero:πππ ππ ππ πPart (b)(ii)We use the quadratic formula, given as π π2 4πππ₯ 2πSubstitute for(where ππ₯ 2 ππ₯ π 0)π 5, π 8, π 25hence:8 64 20 25108 2 141 10π± π. ππ(π. π. π©. ) π¨π« π± π. ππ (π. π. π©. )π₯ FOR MORE PAST PAPER QUESTIONS, VISITWWW.SAVEMYEXAMS.CO.UKWrite down the letters in the word above that have,(a) Exactly one line of symmetry[1](b) Rotational symmetry of order 2[1]Solution:Part (a)We can find out which letters in βZEBRAβ have exactly 1line of symmetry like this:Imagine placing a mirror through the centre of eachletter at loads of different angles β a line of symmetry iswhere that mirror would show us the letter we expectto seeFor example, if we placed a mirror vertically down thecentre of βAβ, between the paper and the mirror wewould see βAβ, so it has a line of symmetry down itscentreThis works for E, B and A, so these 3 letters are theanswerPart (b)Rotational symmetry is found by rotating the letter(from the word βZEBRAβ) around an imaginary point,which we place on one of the cornersβOrder 2β means that you could rotate the letter aroundthe imaginary point and it would look the same in 2different positions (see diagram below)The only letter in βZEBRAβ for which we can do this is Zβ so the answer is ZPAGE 11 OF 26
CIE IGCSE MATHEMATICS//05803.2 Construction3.3 SimilarityQuestion 33:Question 34:This diagram shows triangle ABCTriangles CBA and CED are similar.AB is parallel to DE.AB 9 cm, BE 4.8 cm, EC 6 cm and ED k cm.(a) Work out the value of k.(a) Using a straight edge and compasses only,construct the bisector of angle ABC.(b) Rotational symmetry of order 2[2][2][1]Solution:Part (a)(b) The diagram shows two mathematically similarvases.Vase A has height 20 cm and volume 1500 cm3.Vase B has volume 2592 cm3.Calculate h, the height of vase B.[3]Solution:Part (a)The bisector of angle ABC is drawn in blue.Construction lines are orange and green. You needto use a compass to do this construction andensure that construction lines are clearly shown.Part (b)Using a rule measure carefully 3cm from line AC toconstruct a parallel line inside the triangle asshown.If we imagine that triangle ABC was shortened to createtriangle CED then the factor by which CB was shortenedto create CE is the same factor that shortened AB tomake DE.πΆπ΅ 10.8πΆπΈ 6Thus the scale factor isπΆπΈ 5 πΆπ΅ 9Apply this factor to AB5π·πΈ π΄π΅95 π 9 9 πPAGE 12 OF 26
CIE IGCSE MATHEMATICS//0580Part (b)Part (b)The volume scale factor is2592 1.7281500This is the volume scale factor is the cube of the length(height) scale factor. The height scale factor is therefore63 1.728 5And hence6βπ΅ βπ΄5 ππA line of symmetry is an imaginary line where you canfold the image and have both halves match exactly.Hence by inspection we can see that there are no linesof symmetry as the image will differ if folded over anyimaginary line. 6 such examples are shown below:3.4 Symmetry (in circles)Question 35:This diagram shows triangle ABCThe number of lines of symmetry 03.5 Angles (Circles, Quadrilaterals, Polygons& Triangles)Question 36:(a)(a) The order of rotational symmetry(b) The number of lines of symmetry[1][1]Solution:Part (a)The order of rotational symmetry of a shape is thenumber of times it can be rotated around a full circleand still look the same. Hence by inspection we can seethat:In the diagram, D is on AC so that angle ADB angleABC.i.Show that angle ABD is equal to angle ACB. [2]ii.Complete the statement.Triangles ABD and ACB are [1]iii.AB 12 cm, BC 11 cm and AC 16 cm.Calculate the length of BD.[2]The order of rotational symmetry 6PAGE 13 OF 26
CIE IGCSE MATHEMATICS//0580Solution:(b)Part (a)(i)The sum of the interior angles of the two triangles (ABDand ACB) must equal each other (and 180 ).π΄π΅π· π΄π·π΅ π·π΄π΅ π΄π΅πΆ π΄πΆπ΅ πΆπ΄π΅The angles CAB and DAB are actually one and the sameas D line on AC.π΄π΅π· π΄π·π΅ π΄π΅πΆ π΄πΆπ΅Angles ADB angle ABC.Therefore: π¨π©π« π¨πͺπ©Part (a)(ii)As the angles in these two triangles are the sa
MATHS 0580 ZNOTES x SAVE MY EXAMS // IGCSE SERIES www.savemyexams.co.uk www.znotes.org. TABLE OF CONTENTS 2 CHAPTER 1 Numbers 5 CHAPTER 2 Algebra and Graphs 11 CHAPTER 3 Geometry 16 CHA
IGCSE First Language English 12 IGCSE World Literature 13 IGCSE English as a Second Language 14 . IGCSE Business Studies 19 IGCSE Global Perspectives 21 IGCSE Geography 22 IGCSE History 23 IGCSE Sciences 24 IGCSE Cambridge Mathematics Extended & Core 26 . At BISP, Year 12 and 13 (Key Stage Five) students study the IB Diploma Programme (IBDP .
MARK SCHEME for the June 2004 question papers 0580/0581 MATHEMATICS 0580/01, 0581/01 Paper 1 (Core), maximum raw mark 56 0580/02, 0581/02 Paper 2 (Extended), maximum raw mark 70 0580/03, 0581/03 Paper 3 (Core), maximum raw mark 104 0580/04, 0581/04 Paper 4 (Extended), maximum raw mark 130
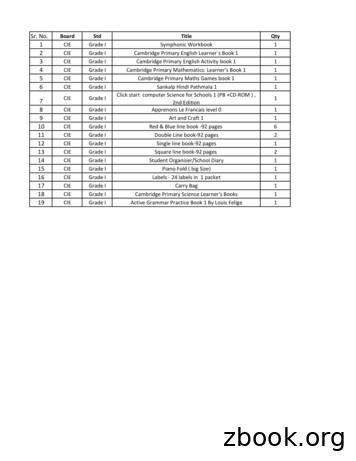
Sr. No. Board Std Title Qty 1 CIE Grade II Cambridge Primary English Learners Book 2 1 2 CIE Grade II Cambridge Primary English Activity book 2 1 3 CIE Grade II Cambridge Primary Mathematics: Learner's Book 2 1 4 CIE Grade II Cambridge Primary Maths Games book 2 1 5 CIE Grade II Sankalp Hindi Pathmala 2 1 6 CIE Grade II Click start computer Sc
IGCSE ARABIC for Native Arabic Speakers - Edexcel 11 GCSE ART & DESIGN - Edexcel 13 IGCSE BUSINESS STUDIES - Cambridge 15 IGCSE ECONOMICS - Cambridge 17 IGCSE COMPUTER SCIENCE - Cambridge 19 GCSE DRAMA - Edexcel 20 IGCSE ENGLISH LANGUAGE - Cambridge 22 IGCSE ENGLISH LITERATURE - Edexcel 22 IGCSE GEOGRAPHY - Edexcel 25
Scheme of work β Cambridge IGCSE Mathematics (0580) from 2015 v1.0 4Y11 Cambridge IGCSE Mathematics (0580) β from 2015 6 Unit 1: Number Recommended prior knowledge Learners should be able to add, subtract, multipl
Schools currently teaching the CIE IGCSE should be able to continue with the same schemes of work as long as they are modified to reflect the changes in content. The table below shows how the content of the Cambridge International Examinations (CIE) IGCSE in Physics qualification (0625) maps onto the Edexcel IGCSE in Physics. Legacy CIE Comment
University of Cambridge International Examinations London GCE AS/A-Level / IGCSE / GCSE Edexcel International. 6 Examination Date in 2011 Cambridge IGCSE Oct/Nov X 9 Cambridge GCE / May/Jun 9 9 London GCE London GCSE May/Jun 9 X Chinese London IGCSE Jan X 9 Cambridge IGCSE / May/Jun 9 9 London IGCSE London GCE Jan 9 9 Cambridge GCE Oct/Nov X 9 Private Candidates School Candidates Exam Date. 7 .
par catΓ©gorie alimentaire. A partir des informations disponibles dans les listes dβingrΓ©dients, il est parfois dΓ©licat pour un mΓͺme libellΓ© dβingrΓ©dient de diffΓ©rencier son utilisation en tant quβadditif ou en tant que substance Γ usage dβenrichissement (exemple : acide ascorbique). Pour ce rapport et pour ces substances, il a Γ©tΓ© dΓ©cidΓ©, par convention (choisie), de .
