Innovative System Identification Methods For Monitoring Applications
Proceedings of the 9th International Conference on Structural Dynamics, EURODYN 2014Porto, Portugal, 30 June - 2 July 2014A. Cunha, E. Caetano, P. Ribeiro, G. Müller (eds.)ISSN: 2311-9020; ISBN: 978-972-752-165-4Innovative System Identification Methods for Monitoring ApplicationsP. Guillaume1, W. Weijtjens, M. Elkafafy, T. De Troyer, C. Devriendt, and G. De Sitter1Department of Mechanical Engineering, Faculty of Engineering SciencesVrije Universiteit Brussel, Pleinlaan 2, B-1050 Brusselsemail: patrick.guillaume@vub.ac.beABSTRACT: Monitoring the modal parameters of civil and mechanical system received plenty of interest the last decades.Several approaches have been proposed and successfully applied in civil engineering for structural health monitoring of bridges(mainly based on the monitoring of the resonant frequencies and mode shapes). In applications such as the monitoring ofoffshore wind turbines and flight flutter testing the monitoring of the damping ratios are essential. For offshore wind turbinemonitoring the presence of time-varying harmonic components, close to the modes of interest, can complicate the identificationprocess. The difficulty related to flight flutter testing is that, in general, only short data records are available.The aim of this contribution is to introduce system identification methods and monitoring strategies that result in more reliabledecisions and that can cope with complex monitoring applications. Basic concepts of system identification will be recapitulatedwith attention for monitoring aspects. The proposed monitoring methodology is based on the recently introducedTransmissibility-based Operational Modal Analysis (TOMA) approach.KEY WORDS: System Identification; Experimental Modal Analysis; Operational Modal Analysis; Transmissibility-basedOperational Modal Analysis; Monitoring.!1.INTRODUCTIONThe application of system identification [1,2] to vibratingstructures resulted some 40 years ago in a new researchdiscipline in mechanical engineering known as "ExperimentalModal Analysis" (EMA) [3-5]. EMA identification methodsand procedures are limited to forced excitation laboratory testswhere the applied forces can be measured together with theresponse of the structure (e.g., accelerations).Today, EMA has become a widespread means of finding themodes of vibration of a machine or structure (e.g., modalanalysis of a body-in-white of a car, Ground-Vibration-Testingof an airplane).In many applications, however, the vibration measurementshave to be performed in “operational” conditions where thestructure is excited by the natural (ambient) excitationsources. In such a case, it is practically impossible to measurethe input forces, and consequently, only output signals(accelerations, strains, ) can be measured. These outputmeasurements are often very noisy (e.g., modal analysis of anairplane during flight, which is also known as flight flutteranalysis). Moreover, the modal parameter estimates (i.e, theresonance frequency, the damping ratios and the mode shapevector of every mode of interest) will depend on theoperational conditions. This makes the modelling processmore complex, but the results are more realistic (i.e., closer toreality) than the ones obtained in laboratory conditions (e.g.,during GVT of an airplane the aero-elastic coupling, which ispresent in flight conditions, is neglected). This field ofresearch is called “Operational Modal Analysis” (OMA) [6,7].Operational Modal Analysis has many advantages. Duringin-operation tests, the real loading conditions are present. Asall real-world systems are to a certain extent non-linear, themodels obtained under real loading will be linearised for morerepresentative working points. Additionally, they will properlytake into account the environmental influences on the systembehaviour (pre-stress of suspensions, load-induced stiffening,aero-elastic interaction, ).Furthermore, the availability of in-operation establishedmodels opens the way for in situ model-based diagnosis anddamage detection (“Structural Health Monitoring”). Hence, aconsiderable interest exists for techniques able to extract validmodels directly from operational data.In this contribution an overview will be given of the basicconcepts of different system identification approaches that canbe used for monitoring applications. This overview will berestricted to frequency-domain estimators. Most of the resultscan be implemented in the time domain too [8]. Next, theTransmissibility-based Operational Modal Analysis will berevisited and new results will be illustrated with attention tomonitoring applications.2.EMA: EXPERIMENTAL MODAL ANALYSIS2.1.Frequency response data driven approachTraditionally, EMA starts with the nonparametricidentification of the frequency respons matrix (FRM) betweenthe applied forces (inputs) and the resulting vibrations(outputs). The H1 or more advanced nonparametric estimatorscan be used to obtain the frequency respons matrix estimate! [ Ĥ (ω k )] at the angular frequencies! ω k with ! k 1, ,nF .Frequency-domain parametric modal estimators, such as theLSCF and the PolyMAX estimators, use rational transferfunction models [9-11]. The parameters to be estimated arethus the numerator and denominator polynomial coefficients.For simplicity of explanation, a common-denominator transferfunction model will be used,!! [H ({α },{β }, ω k )] [N({β }, ω k )]d({α }, ω k )(1)125
Proceedings of the 9th International Conference on Structural Dynamics, EURODYN 2014with ! d({α }, ω k ) a0 Ω 0 (ω k ) an Ω n (ω k ) the denominatorpolynomial and!! N [r ] ({β }, ω k ) b0[r ]Ω 0 (ω k ) bn[r ]Ω n (ω k )!(2)! {N({β }, ω k )} vec([N({β }, ω k )])(3)the numerator polynomial corresponding with the r-th entry ofthe numerator vector ! {N({β }, ω k )} , defines as,!!The vec-operator transforms a matrix into a vector by stackingthe columns of the matrix. The parameter vector! α in (1) isdefend as!!!!!! {α } {vec([a0 , ,an ])}(4)and! β as {β1 } ! {β } (4)! {β n } H with ! {β r } {vec([b0[r ] , ,bn[r ] ])} and ! nH the length of thevector ! {N({β }, ω k )} , i.e., the number of outputs times thenumber of inputs.The commonly-used basis functions! Ω r (ω k ) are defined as!!!! z r k! Ω r (ω k ) r skwith zk exp(iω kTS )(4)with sk iω kfor, respectively, a discrite-time model and a continuous-timemodel. The variable ! TS stands for the sampling period, i.e.,one over the sampling frequency. Other choices are possiblethat could result in better numerical-conditioned equations orimproved (so-called ‘crystal clear’) stabilisation diagrams[12,13].!!The least-squares estimates of ! α and ! β are obtained byminimising the following cost function! (α̂ , β̂ ) arg min ℓ(α , β )(5)(α , β )with ! ℓ(α , β ) [E(α , β , ω k )] F o,i,k Eo,i (α , β , ω k ) .2!2The operator ! F stands for the Frobenius norm while! [E(α , β , ω k )] is the equation error (matrix).Replacing! [H (α , β , ω k )] in (1) by the measured frequency responsematrix yields[N(β , ω k )](6)d(α , ω k )Equation (6) is not exactly satisfied. The error in (6) is givenby!!!! [ Ĥ (ω k )] 126Input-output data driven approachThe input-output data relationship in the frequency domain isgiven by [14]![N(β , ω k )]{F̂(ω k )}(10)d(α , ω k )This equation is not exactly satisfied due to measurementerrors (noise) in the input-output data. After multiplying theleft and right hand side of (10) with ! d(α , ω k ) , a “linear-inthe-parameters” equation error is obtained! { X̂(ω k )} !!! {E(ω k , α , β )} d(α , ω k ){ X̂(ω k )} [N(β , ω k )]{F̂(ω k )} (11)!An additional advantage of using input-output Fouriercoefficients as primary data is that leakage and transienteffects can be compensated.To do so, one additional“transient” polynomial vector, ! {T (γ , ω k )} , has to be added in(11), yielding [15]! ω αβ!! E(k, , ) d(α , ω k ) X̂(ω k ) N(β , ω k )F̂(ω k ) T (γ , ω k ) (12)For compactness of notation, the vector and matrix bracketshave been omitted. Note that adding the “transient”polynomial vector, ! {T (γ , ω k )} , in (12) is equivalent to addingan “one” in the force vector!!ωω! !!! βγ ω! ω αβ αω!! F̂T (k {F̂( )}k) 1 (13)This additional “1” input entry results in an additional columnin the numerator matrix! NT ( , ,k) [N(β , ω k )] {T (γ , ω k )} (14)It is readily verified that! E(k, , ) d( ,k) X̂(ω k ) N T (β , γ , ω k )F̂T (ω k )(15)! [E(α , β , ω k )] [ Ĥ (ω k )] (7)! d(α , ω k )[ Ĥ (ω k )] [N(β , ω k )](8)2.3.!! [E(α , β , ω k )] d(α , ω k )[ Ĥ (ω k )] [N(β , ω k )](9)Compact formulation of the least-squares solverConsider the column vector ! ε [r ] (α , β , ω k ) defined as!resulting in a “linear-in-the-parameters” equation error!2.2.is equal to (12). This observations can be generalised to allexisting input-output frequency-domain estimators (including,for instance, frequency-domain subspace estimators). To sumup, leakage and transient effects can be dealt with in thefrequency-domain by extending the input vector, ! F̂(ω k ) , withan “1” (for all considered frequencies ! ω k )[N(β , ω k )]d(α , ω k )Note that equation (6) can also be rewritten as!When the equation error is “linear-in-the-parameters” the costfunction minimisation (5) reduces to a linear least-squaresproblem, which is much faster and easier to solve than anonlinear least-squares problem.One possible drawback of using frequency responsematrices as primary data for monitoring application is relatedto the need of using averaging schemes. The averagingprocess requires several time records(thus longermeasurement periods). So, one has to assume that the systemdoes not change (i.e., remains time invariant) within every(longer) time period. If this cannot be guaranteed then aninput-output data driven approach could be considered.! ε [r ] (α , β , ω k ) vec(E [r ] (α , β , ω k ))(16)
Proceedings of the 9th International Conference on Structural Dynamics, EURODYN 2014where ! E [r ] (α , β , ω k ) stands for the r-th row of ! [E(α , β , ω k )] ,and, the column vector ! ε [r ] (α , β )!!! ε!! ! ε [r ] (α , β , ω ) 1 [r ] ε(α,β,ω[r ]2)! (α , β ) (17) ε [r ] (α , β , ω n ) F obtained by stacking (16) for all considered angularfrequencies ! ω k with ! k 1,2, ,nF . Equation (17) can berewritten as a linear function of the parameter vectors!! ε [r ] ({α },{β l }) [Jα[r ] ]{α } [J β[rl ] ]{β r }with!!!(18) {ε [r ] (α , β r )} {α }(19)! [J β[rr ] ] {ε [l ] (α , β r )} {β r }(20)!! [Jα[r ] ] resulting in!!!!! !!!!!θ ε [1] (α , β )1 ε (α , β ) ! ε [nH ] (α , β )nH ! [1] Jα ! [nH ] Jα J β[1]100!00 J β[nn H ]00H [J ]{θ } α β1 ! β nH (21)with!Remark 2: When the conditioning of the equations is anissue (e.g., for rational transfer functions in the Laplacedomain), it is advised to solve the least-squares equationsdirectly from the Jacobian matrices ! Jα[r ] and ! J β[rr ] instead of(23) (or (29)).2.3.2. Compact Jacobian matrix formulationIt can be verified that (28) can be rewritten as [16]!!!!!!nHr 12HrSRr α β r ! Rr J β[rr ]H J β[rr ] , ! Sr J β[rr ]H Jα[r ] , ! Tr Jα[r ]H Jα[r ]!(22)(23)In the solution, the stationary point conditions are satisfied!!!!!!!! ℓ(α , β ) {0} α(24)! ℓ(α , β ) {0} β r(25)(26)Substitution of (26) in (22) yields a cost function that onlydepends on ! α! ℓ(α ) α [M ]αH r 1 Jα[r ]H I J β[rr ][J β[rr ]H J β[rr ] ] 1 J β[rr ]H Jα[r ]nH!(30) r 1 Jα[r ]H J β[rr ] Jα[r ]nHwith ! J β[rr ] I J β[rr ][J β[rr ]H J β[rr ] ] 1 J β[rr ]H an orthogonal projectionmatrix.Note that ! J β[rr ] J β[rr ] [0], [J β[rr ] ]H J β[rr ] and ! [J β[rr ] ]2 J β[rr ] .Thus, (27) can be rewritten as!!!! ℓ(α ) α H [J MH J M ]α J [1] J [1]β1α ! JM ! [nH ] [nH ]J βnH Jα!! !(31) (32)Compact generalised total least-squares formulationTo find a unique least-squares solution a parameter constraintneeds to be imposed. The parameter constraint can be appliedon the parameter vector ! α .Usually one entry of theparameter vector ! α is set equal to one. The parameterconstraint can, in general, be formulated as ! α H [C]α 1 . Theleast-squares solution depends on the imposed constraint.This parameter constraint can be included in the cost functionby using a Lagrange multiplier ! l!!!! ℓ({α },l) α H [M ]α l(α H [C]α 1)(33)In the solution, the stationary point conditions are satisfiedfor ! r 1, ,nH . From (25) one can derive that! β r Rr 1SrαnH2.3.3.2nH α Tr r 1 β r SrHwith[M ] r 1 Jα[r ]H Jα[r ] Jα[r ]H J β[rr ][J β[rr ]H J β[rr ] ] 1 J β[rr ]H Jα[r ]withℓ(α , β ) ε [r ] (α , β r )(28)!!Note that the least-squares cost function (5) can be written as!!! Rr Re[J β[rr ]H J β[rr ] ] ,! Sr Re[J β[rr ]H Jα[r ] ] ,! Tr Re[Jα[r ]H Jα[r ] ] (29)Compact normal matrix formulation!!!!!nHRemark 1: This derivation is valid for generalised transferfunction models with complex-valued coefficients.Thederivation for real-valued coefficients can readily beimplemented by redefining ! Rr , ! Sr , and ! Tr aswith ! { } full parameter vector and ! [J ] a structured Jacobianmatrix. This structure can be exploited to reduce computationtime and memory requirements.2.3.1.! [M ] r 1 Tr SrH Rr 1Sr(27) ℓ({α },l) {0} {α }!!!(34) ℓ({α },l) 0(35) lUsing equation (34), the Lagrange multiplier ! l can be writtenas a function of ! α . Elimination of ! l in (33) gives!!!! ℓ(α ) α H [M ]αα H [C]α(36)127
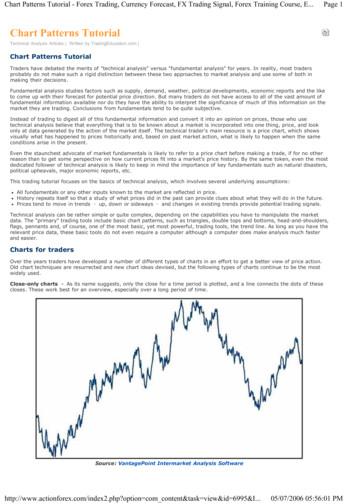
Proceedings of the 9th International Conference on Structural Dynamics, EURODYN 2014So, basically, this means that a least-squares (LS) estimatorcan be reformulated as a generalised total least-squares(GTLS) estimator [17-20].For instance,! [C] [I ] isequivalent withconstrainingthe2-normof! α to one2(! α H α α 2 1 ). Solving the LS problem with the firstcoefficient of ! α constrained to one is equivalent to solvingthe GTLS problem (36) with ! [C] diag(1,0, ,0) .3. OMA: OPERATIONAL MODAL ANALYSISDuring operational modal analysis, the structure remains in itsreal in-operation conditions. These conditions can differsignificantly from the ones obtained during an laboratorycondition forced excitation test. An example is given by highspeed ships where the mass loading of water adjacent to thehull varies with the speed of the ship through the water. Sincechanges in mass loading induce changes in modal parameters,the dynamic behaviour of the ship will depend upon its speed.Other vehicles and structures (bridges open for traffic, cars,agricultural crop sprayer, . . . ) show a similar behaviour tochanges in working condition. Moreover, since all real-worldsystems are to a certain extent non-linear, the models obtainedunder real loading will be linearised in much morerepresentative working points during an in-operation modalanalysis.In practice, EMA estimators can be reused for OMAapplications depending on the preprocessing of the outputonly data. Basically, nonparametric frequency responsfunctions are replaced by nonparametric estimates of the autoand cross power spectra [21].A lot of attention has been paid to the application ofOperational Modal Analysis (OMA) to, for instance, in-flightflutter testing [22-26]. A limitation of this approach is that notall modes of vibration may be well excited by the operationalforces (turbulences). Nevertheless it is desired to identify allcritical flutter modes. When the aircraft is equipped with flyby-wire control, it is quite easy to apply an input signal.Although this input signal is not fully coherent with theapplied forces (mainly due to non-linear effects), it should beused when available. In such cases, one typically usesclassical Experimental Modal Analysis (EMA) identificationtechniques to estimate the modal parameters from the inputoutput (or FRF) measurements.This standard approach is however not advisable for flightflutter testing. Indeed, by doing so, the operational forces dueto the turbulences will be treated as disturbing “noise”.Traditional EMA techniques will remove this “noise”contribution by averaging the measurements. It has beenshown that it is possible to identify modal parameters fromthis so-called noise contribution with an output-only approach(OMA), and so, useful information is lost with an EMAapproach. On the other hand, the OMA identificationtechniques do not use the measured inputs (they use outputonly data) resulting again in a loss of information. Toconclude, none of the EMA and OMA approaches exploit theavailable data in an optimal way. Clearly, to make an optimaluse of the data, a new identification strategy is required thattakes into account the contribution to the output of bothmeasured and unmeasured forces.This concept has been called OMAX (Operational ModalAnalysis in presence of eXogenous input signals), and itspossible application to flight flutter testing as well as otherapplications, has been investigated [27,28].128Note that the input-output data driven approach (Sec. 2.2.)partially fits in the OMAX concept. Equation (11) can bereformulated as!!N(β , ω k )1F̂(ω k ) E(ω k , α , β ) (37)d(α , ω k )d(α , ω k )where ! F̂(ω k ) represents the known forces and ! E(ω k , α , β )the unknown operational forces. The transfer function from! E(ω k , α , β ) to ! X̂(ω k ) only takes into account the commondenominator polynomial ! d(α , ω k ) .A more general approach is obtained by adding thenumerator ! M ( χ , ω k )! X̂(ω k ) !N(β , ω k )M ( χ ,ω k )F̂(ω k ) E(ω k , α , β ) (38)d(α , ω k )d(α , ω k )Unknown transient excitation can readily be included too! X̂(ω k ) !! ω!!!θN T (β , γ , ω k )M ( χ ,ω k )F̂T (ω k ) E(ω k , α , β ) (39)d(α , ω k )d(α , ω k )resulting in the following equation error! X̂(k) d(α , ω k ) X̂(ω k ) N T (β , γ , ω k )F̂T (ω k )(40)M ( χ ,ω k )with ! the parameter vector containing (! α , β , γ , χ ). As (40) isa nonlinear function of ! χ , nonlinear optimisation tools arerequired to obtain the parameter vector estimate ! θˆ .! E(ω k ,θ ) 4.TRANSMISSIBILITY-BASED OMA APPROACHIt has been shown that transmissibility functions can be usedto identify modal parameters using output-only data [29,30].One important advantage of this approach is that the forcesare eliminated from the equations, i.e. the unknownoperational forces can be arbitrary (persistently exciting)signals. It can even be applied in presence of harmoniccomponents [31,32].!Consider a multiple degree-of-freedom system described by! [Ms 2 Cs K ]{X(s)} {F(s)}!(41)The eigenvalues ! λ m (system poles) and eigenvectors ! {φm }(mode shapes) satisfy the generalised eigenvalue equations!! [Z(λ m )]{φm } {0}(42)!λwith ! [Z( )] [M λ 2 C λ K ] . This eigenvalue problem canbe reformulated as an optimisation problem [33]. Considerthe following cost function!! ℓ(λ ,{φ }) [Z(λ )]{φ }!2(43)The eigenvalues ! λ m and corresponding eigenvectors ! {φm }are the minima of this cost function (! ℓ(λ m ,{φm }) 0 ). Toavoid the trivial solution (! {φ } {0} ), the 2-norm of ! {φ } isconstraint to one.The cost function (43) is illustrated in Figure 1. Twominima can be clearly observed corresponding with the polesof the first and second mode. The cost function is plottedversus the real and imaginary part of ! λ . For every value of ! λthe corresponding value of ! {φ } resulting in the lowest valueof the cost function (43) is used to construct Figure 1 [33].!
Proceedings of the 9th International Conference on Structural Dynamics, EURODYN 2014!!Figure 4. Minimum value of (54) versus ! λ with ! φ φ1 .Figure 1. Minimum value of cost function (43) versus ! λ .!!Figure 5. Minimum value of (54) versus ! λ with ! φ φ2 .Figure 2. Minimum value of cost function (50) versus ! λ .!!Figure 3. Minimum value of cost function (53) versus ! λ .!Figure 6. Minimum value of (54) versus ! λ with ! φ φ1 for anincrease (doubling) of the damping matrix C.!129
Proceedings of the 9th International Conference on Structural Dynamics, EURODYN 2014Consider the case where the system is excited with, say, oneforce!!!!!! Z11 (ω k ) Z12 (ω k ) ! Z1n (ω k )X Z (ω ) Z 22 (ω k ) ! Z 2nX (ω k )! 21 k!!! Z n 1 (ω k ) Z n 2 (ω k ) ! Z n n (ω k )XXX X X (ω ) 1 k X2 (ω k ) ! XnX (ω k ) This can be reformulated as! [Z(ω k )]{X(ω k )} {Q}F1 (ω k ) ,!!! F1 (ω k ) 0 ! 0 ! {Q} 10!0 (44)(45)Left multiplication with the orthogonal projection matrix! [Q ] [I ] {Q}[{Q} H {Q}] 1 {Q} H gives!!!!!!with! [Q ][Z(ω k )]{X(ω k )} {0}(46) 00!0 Z(ω)Z(ω)!Z(ω k )21k22k2nX ! [Q ][Z(ω k )] !!! Z nX 1 (ω k ) Z nX 2 (ω k ) ! Z nX nX (ω k )Thus (46) reduces towith!!!! ! [Z L1 (ω k )]{X(ω k )} {0}(47) Z 21 (ω k ) Z 22 (ω k ) ! Z 2n (ω k )X !!! Z (ω ) Z (ω ) ! Z (ω )n1kn2knnkXX X X! [Z L1 (ω k )] (49)!is plotted in Figure 2. One notices that the correct poles aremissing. To find a unique solution the matrix ! [Z(λ m )] in (43)has to be a full column rank matrix. This is not the case for! [Z L1 (λ m )] as the first row of ! [Z(λ m )] is missing. With otherwords, there are not enough equations to find the unknownparameters.One possible approach consists in increasing the amount ofequations. This can be done by considering a second loadingcondition. The force will now be applied in, say, location 2.This will result in the following matrix (where the second rowof ! [Z(λ m )] is now missing)!!!!!!!! Z11 (ω k ) Z12 (ω k ) ! Z1n (ω k )X Z 31 (ω k ) Z 32 (ω k ) ! Z 3nX (ω k )! [Z L 2 (ω k )] !!! Z nX 1 (ω k ) Z nX 2 (ω k ) ! Z nX nX (ω k ) (51)Combining the equations of both loading conditions gives Z L1 (λ ) {φ }! ℓ(λ ,{φ }) Z L 2 (λ ) !!(52)2All rows of ! [Z(λ m )] are now again included resulting in thecorrect cost function given in Figure 1.130! {φ } (53)2! ℓ(λ ) [Z L1 (λ )]{φm }(54)2The solution for the first and second mode are given in Figure4 and Figure 5, respectively. Note that only one loadingcondition is sufficient to estimate the resonant frequency anddamping ratio of every mode of interest (for normal as well ascomplex mode shapes).The polynomial matrix ! [Z L1 (λ )] can be derived fromoutput-only measurements. Indeed,(50)2 Re(Z L1 (λ ))! ℓ(λ ,{φ }) Im(Z L1 (λ ))The amount of equations (rows) doubled but they are nowreal-valued instead of complex-valued. Only the poles remaincomplex-valued. The corresponding cost function is plottedin Figure 3. One observes that there is an infinite number ofpossible solutions. Indeed, all poles lying on the (yellowgreen) curve are possible solutions. Note that this curvepasses through the correct poles.In many monitoring applications the poles are subjected tolarger changes that the mode shapes. If the mode shapes ofthe modes of interests are a-priori known, the correspondingpoles can be obtain by minimising!!The resulting cost function! ℓ(λ ,{φ }) [Z L1 (λ )]{φ }!!!!!(48)!Another possible approach consists is reducing the amount ofunknowns. For instance, for normal modes, one can imposethe eigenvectors to be real-valued instead of complex-valued.Doing so for one loading condition (e.g., L1) results in thefollowing cost function Z 21 ! " Z nX 1!Z 22"Z nX 2 XZ 2nX 1 X2" !! Z nX nX XnX ! 0 ! 0 (55)can be transformed into a multivariable transmissibilityfunction. Rewriting (55) as!!!!!!!! Z 21 ! ! Zn 1 X Z 22 ! Z 2n X " X1 " Z ! Z nX nX nX 2 X2 ! ! XnX Z 22 ! Z 2n X " " Z ! Z nX nX nX 2 X 2 ! X nX 0 ! 0 (56)gives 1 Z 21 ! Zn 1 X X1 (57)Thus, an input-output estimator, with as input the (arbitrary)reference output ! X1 and as output vector the remainingoutputs, can be used to derive all necessary polynomialfunctions. The number of required reference outputs equalson the number of independent (operational) forces. It isreadily verified that the number of rows of the matrix! [Z L1 (λ )] equals the number of outputs ! n X minus the numberof (independent) input forces.If there are several independent (and unknown) forcesactive, the number of row of the matrix could be small.Assume that the number of (independent) forces equals! n X 1 . In that case the matrix ! [Z L1 (λ )] will reduce to a row
Proceedings of the 9th International Conference on Structural Dynamics, EURODYN 2014vector of size ! 1 n X . Even then the minimum of the costfunction (54) turns out to be reached in the correct pole.Figure 6 shows what happens when the damping increases.The minimum of the cost function tracks the correct value ofthe pole. It is assumed here that the mode shape does notchange. The validity of this assumption can be verified bymeans of the cost function. Indeed, a violation of thisassumption would result in an increase of the cost functionvalue.5.CONCLUSIONSIn this contribution an overview has been given of the basicconcepts of different system identification approaches that areused for monitoring applications. This overview was restrictedto frequency-domain estimators but most results can beextended to the time domain. Eventually, the Transmissibilitybased Operational Modal Analysis has been revisited withattention to monitoring applications and new results has .3.4.5.6.7.8.9.10.11.12.13.14.L. Ljung (1999). System Identification: Theory for the User. PrenticeHall: Upper Saddle River.R. Pintelon and J. Schoukens (2012). System Identification A FrequencyDomain Approach, 2nd edition. Wiley-IEEE Press.Maia N., “Theoretical and Experimental Modal Analysis.” MechanicalEngineering Research Studies. Engineering Control Series 9, 1997.W. Heylen, S. Lammens and P. Sas (2007). Modal Analysis: Theory andTesting. KU Leuven.D.J. Ewins D.J (2000). Modal testing: theory, practice, and application.”Research Studies Press.Reynders, E., “System Identification Methods for (Operational) ModalAnalysis: Review and Comparison,” ARCHIVES OFCOMPUTATIONAL METHODS IN ENGINEERING. Vol. 19((1), pp.51-124, 2012.R. Brinckers (2014). Introduction to Operational Modal Analysis.Wiley-Blackwell.Guillaume, P., De Troyer, T., Deckers, K., Vanlanduit, S., Time-domainimplementation of the least-squares complex frequency-domainestimator for on-line identification of modal parameters, ICED2007International Conference on Engineering Dynamics, 16-18 April 2007,Carvoeiro, Portugal.Guillaume P., P. Verboven and S. Vanlanduit, “Frequency-DomainMaximum Likelihood Estimation of Modal Parameters with ConfidenceIntervals”, Proceedings of the International Conference on Noise andVibration Engineering (ISMA-23), Leuven (Belgium), September16-18, pp. 359-366, 1998.Guillaume P, P. Verboven, S. Vanlanduit, H. Van der Auweraer and B.Peeters, “A Poly-reference Implementation of the Least-SquaresComplex Frequency-domain Estimator”, Proceedings of the 21thInternational Modal Analysis Conference, Orlando, Florida (USA),February 3-6, 2003.Peeters, B., Van der Auweraer, H., Guillaume, P., and Leuridan, J., "ThePolyMAX frequency-domain method: a new standard for modalparameter estimation?," SHOCK AND VIBRATION SN 1070-9622,11(3-4), pp. 395-409, 2004.Van Der Auweraer H., P. Guillaume, P. Verboven and S. Vanlanduit,“Application of a fast-stabilizing frequency domain parameteridentification method,” ASME Journal of Dynamic Systems,Measurement, and Control, vol. 123, no. 4, pp. 651-658, 2001.Cauberghe, B., Guillaume, P., Verboven, P., Vanlandult, S., and Parloo,E., "The influence of the parameter constraint on the stability of thepoles and the discrimination capabilities of the stabilisation diagrams,"MECHANICAL SYSTEMS AND SIGNAL PROCESSING SN0888-3270, 19(5), pp. 989-1014, SEP, 2005.Verboven, P., Guillaume, P., Cauberghe, B., Vanlanduit, S., and Parloo,E., "Modal parameter estimation from input-output Fourier data usingfrequency-domain maximum likelihood identification," JOURNAL OFSOUND AND VIBRATION SN 0022-460X, 276(3-5), pp. 957-979,SEP 22, 2004.22.23.24.25.26.27.28.29.30.31.32.33.!R Pintelon, J Schoukens, G Vandersteen, “Frequency domain systemidentification using arbitrary signals,” IEEE Transactions on AutomaticControl 42 (12), 1717-1720, 1997.Verboven, P., Guillaume, P., and Cauberghe, B., "Multivariablefrequency-response curve fitting with application to modal parameterestimation," AUTOMATICA SN 0005-1098, 41(10), pp. 1773-1782,OCT, 2005.Pintelon R., P. Guillaume, G. Vandersteen and Y. Rolain, “Analysis,Development and Applications of TLS Algorithms in FrequencyDomain System Identification”, SIAM J. Matrix Anal. Appl., vol. 19,no. 4, pp. 983-1004, 1998.S. Van Huffel and J. Vandewalle (1991). The Total Least SquaresProblem, SIAM.Verboven P., P. Guillaume and E. Parloo. “Frequency-Domain TLS andGTLS Algorithms for Modal Analysis Applications”, chapter in: TotalLeast Squares and Errors-in-Variables Modeling: Analysis, Algorithmsand Applications, edited by S. Vanhuffel and Phillipe Lemmerling,Kluwer Academic Publishers, Dordrecht (the Netherlands), pp. 301-314,2002.Guillaume P., R. Pintelon and J. Schoukens, “A Weighted Total LeastSquares Estimator for Multivariable Systems with Nearly MaximumLikelihood Properties”, IEEE Trans. Instrum. Meas., vol. 47, no. 4, pp.818-822, 1998.B. Peeters and H. Van der Auweraer, "PolyMAX: a revolution inOperational Modal Analysis," Proceedings of IOMAC, the 1stInternational Operational Modal Analysis Conference, Copenhagen,Denmark, 26-27 April 2005.Verboven, P., E. Parloo, P. Guillaume and M. Van Overmeire."Autonomous Structural Health Monitoring - Part 1: Modal ParameterEstimation and Tracking." MECHANICAL SYSTEMS AND SIGNALPROCESSING 16, no. 4 (2002): 637-57.Parloo, E., P. Verboven, P. Guillaume and M. Van Overmeire."Autonomous Structural Health Monitoring - Part II: Vibration-basedIn-operation Damage Assessment." MECHANICAL SYSTEMS ANDSIGNAL PROCESSING 16, no. 4 (2002): 659-75.Parloo, E., P. Guillaume and B. Cauberghe. "Maximum LikelihoodId
KEY WORDS: System Identification; Experimental Modal Analysis; Operational Modal Analysis; Transmissibility-based Operational Modal Analysis; Monitoring. ! 1. INTRODUCTION The application of system identification [1,2] to vibrating . Vrije Universiteit Brussel, Pleinlaan 2, B-1050 Brussels email: patrick.guillaume@vub.ac.be
Bruksanvisning för bilstereo . Bruksanvisning for bilstereo . Instrukcja obsługi samochodowego odtwarzacza stereo . Operating Instructions for Car Stereo . 610-104 . SV . Bruksanvisning i original
10 tips och tricks för att lyckas med ert sap-projekt 20 SAPSANYTT 2/2015 De flesta projektledare känner säkert till Cobb’s paradox. Martin Cobb verkade som CIO för sekretariatet för Treasury Board of Canada 1995 då han ställde frågan
service i Norge och Finland drivs inom ramen för ett enskilt företag (NRK. 1 och Yleisradio), fin ns det i Sverige tre: Ett för tv (Sveriges Television , SVT ), ett för radio (Sveriges Radio , SR ) och ett för utbildnings program (Sveriges Utbildningsradio, UR, vilket till följd av sin begränsade storlek inte återfinns bland de 25 största
Hotell För hotell anges de tre klasserna A/B, C och D. Det betyder att den "normala" standarden C är acceptabel men att motiven för en högre standard är starka. Ljudklass C motsvarar de tidigare normkraven för hotell, ljudklass A/B motsvarar kraven för moderna hotell med hög standard och ljudklass D kan användas vid
LÄS NOGGRANT FÖLJANDE VILLKOR FÖR APPLE DEVELOPER PROGRAM LICENCE . Apple Developer Program License Agreement Syfte Du vill använda Apple-mjukvara (enligt definitionen nedan) för att utveckla en eller flera Applikationer (enligt definitionen nedan) för Apple-märkta produkter. . Applikationer som utvecklas för iOS-produkter, Apple .
och krav. Maskinerna skriver ut upp till fyra tum breda etiketter med direkt termoteknik och termotransferteknik och är lämpliga för en lång rad användningsområden på vertikala marknader. TD-seriens professionella etikettskrivare för . skrivbordet. Brothers nya avancerade 4-tums etikettskrivare för skrivbordet är effektiva och enkla att
Den kanadensiska språkvetaren Jim Cummins har visat i sin forskning från år 1979 att det kan ta 1 till 3 år för att lära sig ett vardagsspråk och mellan 5 till 7 år för att behärska ett akademiskt språk.4 Han införde två begrepp för att beskriva elevernas språkliga kompetens: BI
**Godkänd av MAN för upp till 120 000 km och Mercedes Benz, Volvo och Renault för upp till 100 000 km i enlighet med deras specifikationer. Faktiskt oljebyte beror på motortyp, körförhållanden, servicehistorik, OBD och bränslekvalitet. Se alltid tillverkarens instruktionsbok. Art.Nr. 159CAC Art.Nr. 159CAA Art.Nr. 159CAB Art.Nr. 217B1B