For The Class Of Bernoulli Shifts We Prove Here That Is-PDF Free Download
May 02, 2018 · D. Program Evaluation ͟The organization has provided a description of the framework for how each program will be evaluated. The framework should include all the elements below: ͟The evaluation methods are cost-effective for the organization ͟Quantitative and qualitative data is being collected (at Basics tier, data collection must have begun)
Silat is a combative art of self-defense and survival rooted from Matay archipelago. It was traced at thé early of Langkasuka Kingdom (2nd century CE) till thé reign of Melaka (Malaysia) Sultanate era (13th century). Silat has now evolved to become part of social culture and tradition with thé appearance of a fine physical and spiritual .
On an exceptional basis, Member States may request UNESCO to provide thé candidates with access to thé platform so they can complète thé form by themselves. Thèse requests must be addressed to esd rize unesco. or by 15 A ril 2021 UNESCO will provide thé nomineewith accessto thé platform via their émail address.
̶The leading indicator of employee engagement is based on the quality of the relationship between employee and supervisor Empower your managers! ̶Help them understand the impact on the organization ̶Share important changes, plan options, tasks, and deadlines ̶Provide key messages and talking points ̶Prepare them to answer employee questions
Dr. Sunita Bharatwal** Dr. Pawan Garga*** Abstract Customer satisfaction is derived from thè functionalities and values, a product or Service can provide. The current study aims to segregate thè dimensions of ordine Service quality and gather insights on its impact on web shopping. The trends of purchases have
Chapter Outline 1. Fluid Flow Rate and the Continuity Equation 2. Commercially Available Pipe and Tubing 3. Recommended Velocity of Flow in Pipe and Tubing 4. Conservation of Energy –Bernoulli’s Equation 5. Interpretation of Bernoulli’s Equation 6. Restrictions on Bernoulli’s Equation 7. Applications of Bernoulli’s Equation 8 .
Bruksanvisning för bilstereo . Bruksanvisning for bilstereo . Instrukcja obsługi samochodowego odtwarzacza stereo . Operating Instructions for Car Stereo . 610-104 . SV . Bruksanvisning i original
Chính Văn.- Còn đức Thế tôn thì tuệ giác cực kỳ trong sạch 8: hiện hành bất nhị 9, đạt đến vô tướng 10, đứng vào chỗ đứng của các đức Thế tôn 11, thể hiện tính bình đẳng của các Ngài, đến chỗ không còn chướng ngại 12, giáo pháp không thể khuynh đảo, tâm thức không bị cản trở, cái được
MASS, BERNOULLI, AND ENERGY EQUATIONS This chapter deals with three equations commonly used in fluid mechanics: the mass, Bernoulli, and energy equations. The mass equa- tion is an expression of the conservation of mass principle. The Bernoulli equationis concerned with the conservation of kinetic, potential, and flow energies of a fluid stream and their conversion to each other in
Chapter 5 Flow of an Incompressible Ideal Fluid Contents 5.1 Euler’s Equation. 5.2 Bernoulli’s Equation. 5.3 Bernoulli Equation for the One- Dimensional flow. 5.4 Application of Bernoulli’s Equation. 5.5 The Work-Energy Equation. 5.6 Euler’s Equation for Two- Dimensional Flow. 5.7 Bernoulli’s Equation for Two- Dimensional Flow Stream .
10 tips och tricks för att lyckas med ert sap-projekt 20 SAPSANYTT 2/2015 De flesta projektledare känner säkert till Cobb’s paradox. Martin Cobb verkade som CIO för sekretariatet för Treasury Board of Canada 1995 då han ställde frågan
service i Norge och Finland drivs inom ramen för ett enskilt företag (NRK. 1 och Yleisradio), fin ns det i Sverige tre: Ett för tv (Sveriges Television , SVT ), ett för radio (Sveriges Radio , SR ) och ett för utbildnings program (Sveriges Utbildningsradio, UR, vilket till följd av sin begränsade storlek inte återfinns bland de 25 största
Hotell För hotell anges de tre klasserna A/B, C och D. Det betyder att den "normala" standarden C är acceptabel men att motiven för en högre standard är starka. Ljudklass C motsvarar de tidigare normkraven för hotell, ljudklass A/B motsvarar kraven för moderna hotell med hög standard och ljudklass D kan användas vid
LÄS NOGGRANT FÖLJANDE VILLKOR FÖR APPLE DEVELOPER PROGRAM LICENCE . Apple Developer Program License Agreement Syfte Du vill använda Apple-mjukvara (enligt definitionen nedan) för att utveckla en eller flera Applikationer (enligt definitionen nedan) för Apple-märkta produkter. . Applikationer som utvecklas för iOS-produkter, Apple .
Le genou de Lucy. Odile Jacob. 1999. Coppens Y. Pré-textes. L’homme préhistorique en morceaux. Eds Odile Jacob. 2011. Costentin J., Delaveau P. Café, thé, chocolat, les bons effets sur le cerveau et pour le corps. Editions Odile Jacob. 2010. Crawford M., Marsh D. The driving force : food in human evolution and the future.
Le genou de Lucy. Odile Jacob. 1999. Coppens Y. Pré-textes. L’homme préhistorique en morceaux. Eds Odile Jacob. 2011. Costentin J., Delaveau P. Café, thé, chocolat, les bons effets sur le cerveau et pour le corps. Editions Odile Jacob. 2010. 3 Crawford M., Marsh D. The driving force : food in human evolution and the future.
MARCH 1973/FIFTY CENTS o 1 u ar CC,, tonics INCLUDING Electronics World UNDERSTANDING NEW FM TUNER SPECS CRYSTALS FOR CB BUILD: 1;: .Á Low Cóst Digital Clock ','Thé Light.Probé *Stage Lighting for thé Amateur s. Po ROCK\ MUSIC AND NOISE POLLUTION HOW WE HEAR THE WAY WE DO TEST REPORTS: - Dynacó FM -51 . ti Whárfedale W60E Speaker System' .
Glossary of Social Security Terms (Vietnamese) Term. Thuật ngữ. Giải thích. Application for a Social Security Card. Đơn xin cấp Thẻ Social Security. Mẫu đơn quý vị cần điền để xin số Social Security hoặc thẻ thay thế. Baptismal Certificate. Giấy chứng nhận rửa tội
More than words-extreme You send me flying -amy winehouse Weather with you -crowded house Moving on and getting over- john mayer Something got me started . Uptown funk-bruno mars Here comes thé sun-the beatles The long And winding road .
Phần II: Văn học phục hưng- Văn học Tây Âu thế kỷ 14- 15-16 Chương I: Khái quát Thời đại phục hưng và phong trào văn hoá phục hưng Trong hai thế kỉ XV và XVI, châu Âu dấy lên cuộc vận động tư tưởng và văn hoá mới rấ
Food outlets which focused on food quality, Service quality, environment and price factors, are thè valuable factors for food outlets to increase thè satisfaction level of customers and it will create a positive impact through word ofmouth. Keyword : Customer satisfaction, food quality, Service quality, physical environment off ood outlets .
1 hỆ thỐng kiẾn thỨc sinh hỌc 10 phẦn i bài 1. cÁc cẤp tỔ chỨc cỦa thẾ giỚi sỐng a. tÓm tẮt lÝ thuyẾt i. cÁc cẤp tỔ chỨc cỦa thẾ giỚi sỐng các cấp tổ chức của thế giới sống:
Chapter 5 MASS, BERNOULLI AND ENERGY EQUATIONS Lecture slides by Hasan Hacışevki. . Bernoulli equation is also useful in the preliminary design stage. 3. Objectives Apply the conservation of mass equation to balance the incoming and outgoing flow rates in a flow system.
Derive the Bernoulli (energy) equation. Demonstrate practical uses of the Bernoulli and continuity equation in the analysis of flow. Understand the use of hydraulic and energy grade lines. Apply Bernoulli Equation to solve fluid mechanics problems (e.g. flow measurement). K. ALASTAL 2 CHAPTER 6: ENERGY EQUATION AND ITS APPLICATIONS FLUID MECHANICS, IUG
Chapter 5 Venturimeter & Orificemeter Applications of the Bernoulli Equation The Bernoulli equation can be applied to a great many situations not just the pipe flow we have been considering up to now. In the following sections we will see some examples of its application to flow measurement from tanks, within pipes as well as in open channels. 1.
The corresponding random variable is de ned as: De nition (The Bernoulli Distribution) A random variable X has a Bernoulli distribution and it is referred to as a Bernoulli random variable if and only if its probability distribution is given by f (x; q) qx(1 q)1 x for x 0,1 Note that
och krav. Maskinerna skriver ut upp till fyra tum breda etiketter med direkt termoteknik och termotransferteknik och är lämpliga för en lång rad användningsområden på vertikala marknader. TD-seriens professionella etikettskrivare för . skrivbordet. Brothers nya avancerade 4-tums etikettskrivare för skrivbordet är effektiva och enkla att
Den kanadensiska språkvetaren Jim Cummins har visat i sin forskning från år 1979 att det kan ta 1 till 3 år för att lära sig ett vardagsspråk och mellan 5 till 7 år för att behärska ett akademiskt språk.4 Han införde två begrepp för att beskriva elevernas språkliga kompetens: BI
**Godkänd av MAN för upp till 120 000 km och Mercedes Benz, Volvo och Renault för upp till 100 000 km i enlighet med deras specifikationer. Faktiskt oljebyte beror på motortyp, körförhållanden, servicehistorik, OBD och bränslekvalitet. Se alltid tillverkarens instruktionsbok. Art.Nr. 159CAC Art.Nr. 159CAA Art.Nr. 159CAB Art.Nr. 217B1B
produktionen sker på ett reproducerbart sätt. Alla geler som produceras testas därför för att kontrollera att de upprätthåller den kvalité som krävs för produktion av läkemedel. De biologiska läkemedlen kan sorteras på olika egenskaper och för geler som separerar med
An Asahi Kasei Group Company Inledning Den här manualen innehåller handhavandeinstruktioner för webbportalen Senseair Dashboard med dess användare som tänkta läsare. Inledningsvis beskrivs några begrepp som lägger grunden för behörigheter i systemet. Därefter följer steg för steg instruktioner av alla funktioner i systemet.
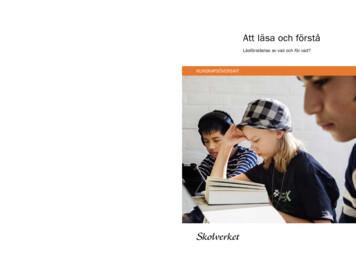
Att läsa och förstå Läsförståelse av vad och för vad? Att läsa och förstå. Skolverket. KUNSKAPSÖVERSIKT KUNSKAPSÖVERSIKT. Forskning visar att läsförståelsen påverkar möjlig heterna att tillägna sig kunskaper i alla skolämnen. Men vad kan skolan göra för att stödja elevers läs förståelse genom hela grundskolan?
This presentation and SAP's strategy and possible future developments are subject to change and may be changed by SAP at any time for any reason without notice. This document is 7 provided without a warranty of any kind, either express or implied, including but not limited to, the implied warranties of merchantability, fitness for a .
Lời Nói Đầu K inh Bát-Nhã (Prajna) đƣợc lƣu hành rất sớm tại Ấn độ. Khoảng 700 năm sau khi Phật diệt độ (cuối thế kỷ II đầu thế kỷ III Tây lịch), lúc Bồ-tát Long Thọ
UNESCO in consultation with thé National Commission for UNESCO as well as b non- overnmental or anizations NGOs in officiai artnershi with UNESCO. Nominations must focus on a s ecific ESD ro'ect or ro ramme. Each Member State or NGO can make u to three nominations for an édition of thé Pri
1.2. Chương Trình 0% Lãi Suất Ưu Đãi Mua Sắm không áp dụng cho Chủ thẻ Tín Dụng Thương Mại. The Installment Plan With 0% Interest is not applicable for HSBC Business Credit Card. 1.3. Loại tiền tệ được sử dụng trong Chương Trình 0% L
For centuries, Baccarat has been privileged to create masterpieces for royal households throughout the world. Honoring that legacy we have imagined a tea service as it might have been enacted in palaces from St. Petersburg to Bangalore. Pairing our menus with world-renowned Mariage Frères teas to evoke distant lands we have
HƯỚNG DẪN LỰA CHỌN DÂY & CÁP HẠ THẾ DÂY & CÁP HẠ THẾ A/ LỰA CHỌN DÂY & CÁP : Khi chọn cáp, khách hàng cần xem xét những yếu tố sau: - Dòng điện định mức - Độ sụt áp - Dòng điện ngắn mạch - Cách lắp đặt - Nhiệt độ môi trường hoặc nhiệt độ đất
Niagara University-Toronto niagara.instructure.com Canada Simon Fraser University Canvas.sfu.ca Canada University of British Columbia (UBC) Canvas.ubc.ca Canada University of Toronto learn.utoronto.ca Canada . 5 Nắm bắt xu thế phát triển công nghệ của thế giới, Trường Đại học Công nghệ .
Joomla có thể dễ dàng cài đặt, dễ dàng quản lý và có độ tin cậy cao. Joomla có mã nguồn mở do đó việc sử dụng Joomla là hoàn toàn miễn phí cho tất cả mọi người trên thế giới. Tham khảo thêm: WikiPedia-Joomla, Wikipedia-Hệ quản trị nội dung Các khái niệm và thuật ngữ